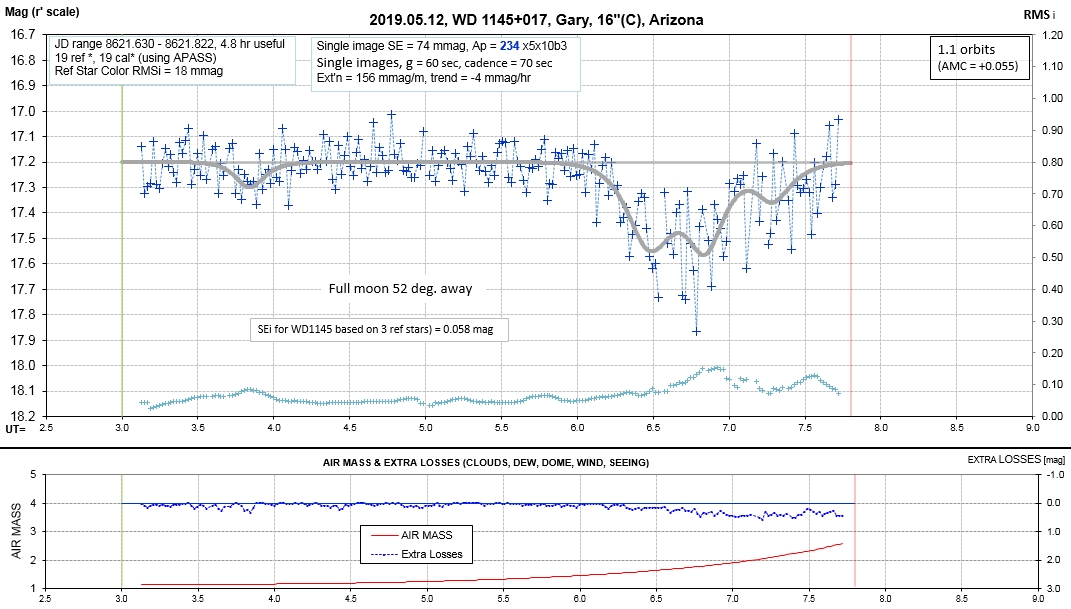
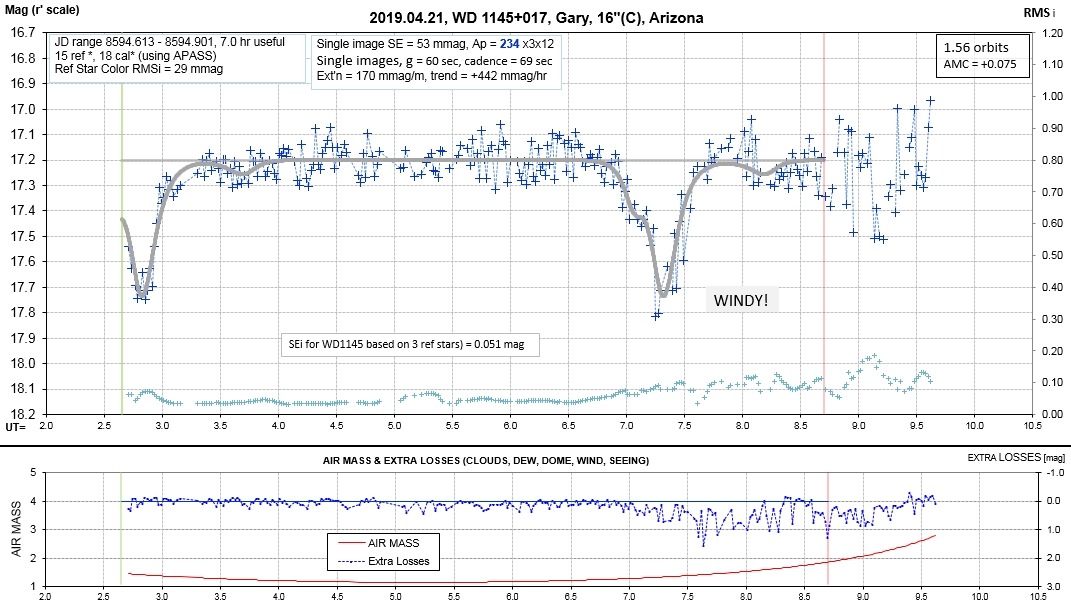
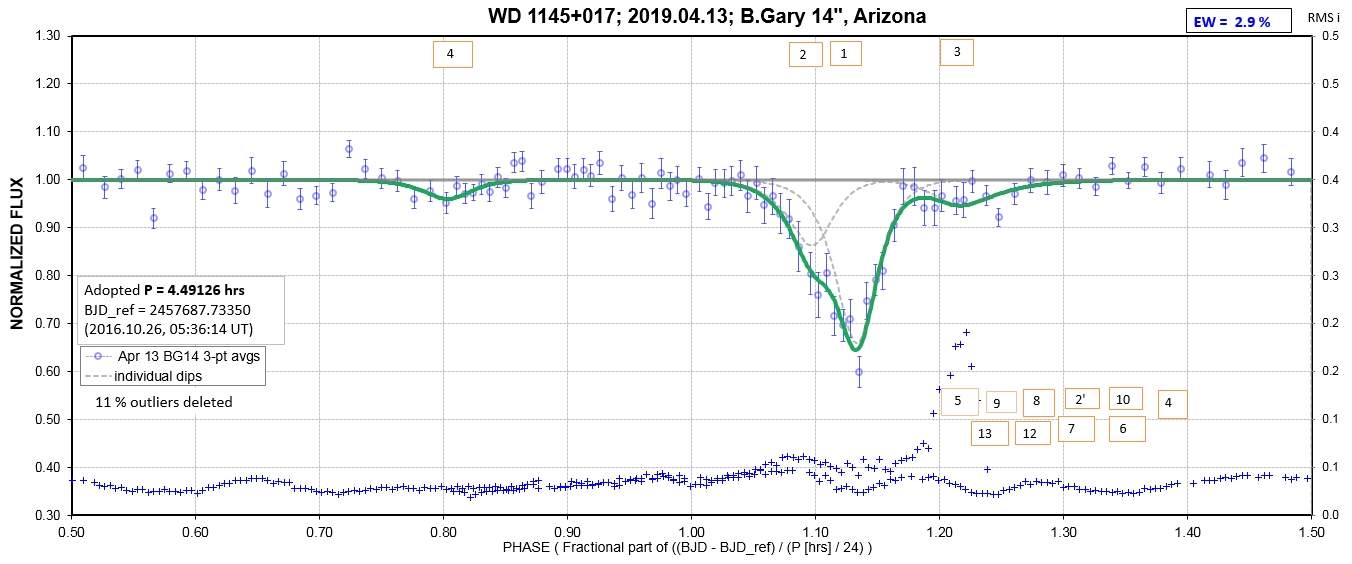
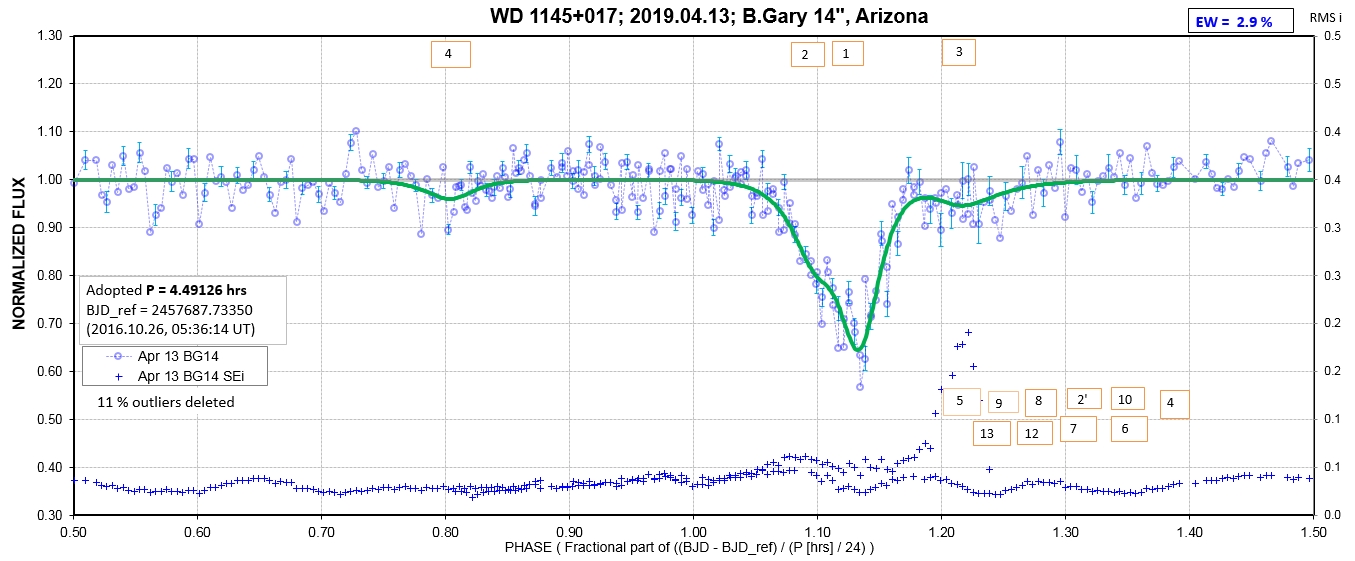
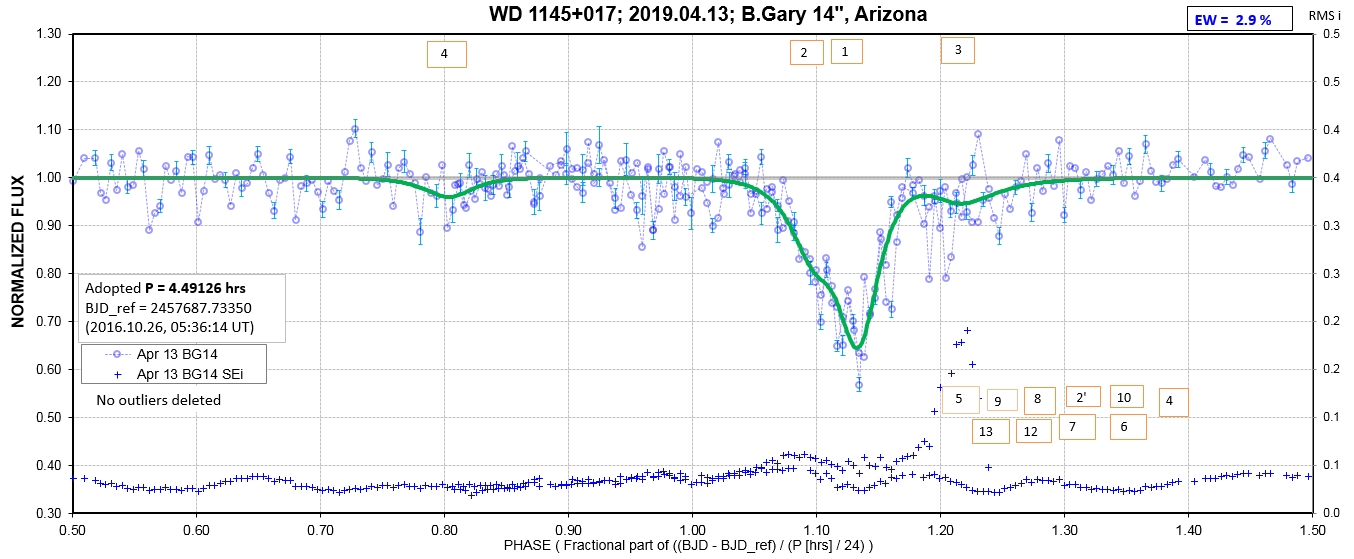
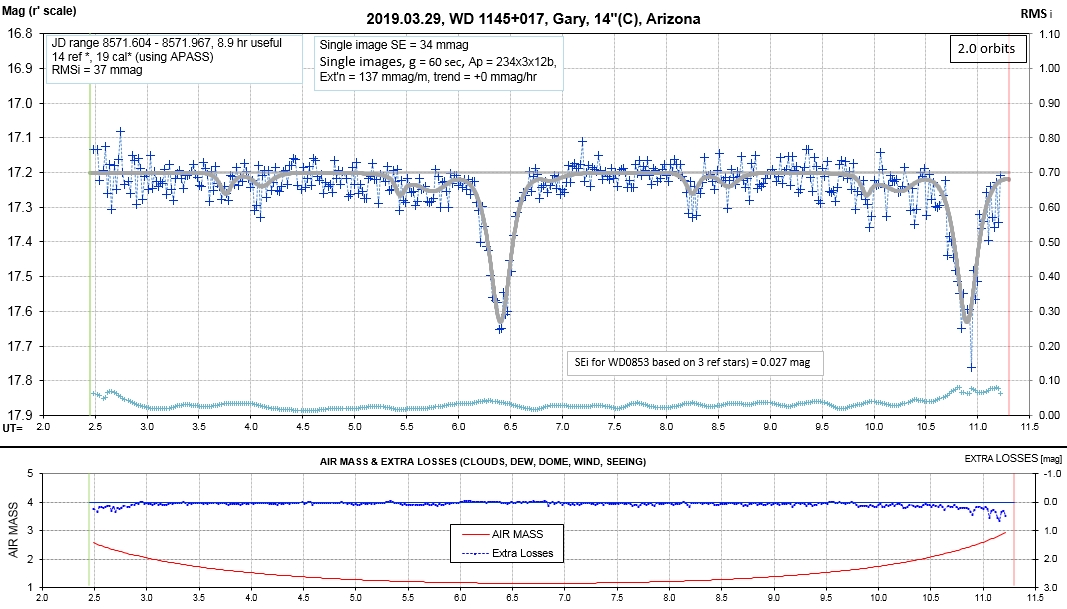
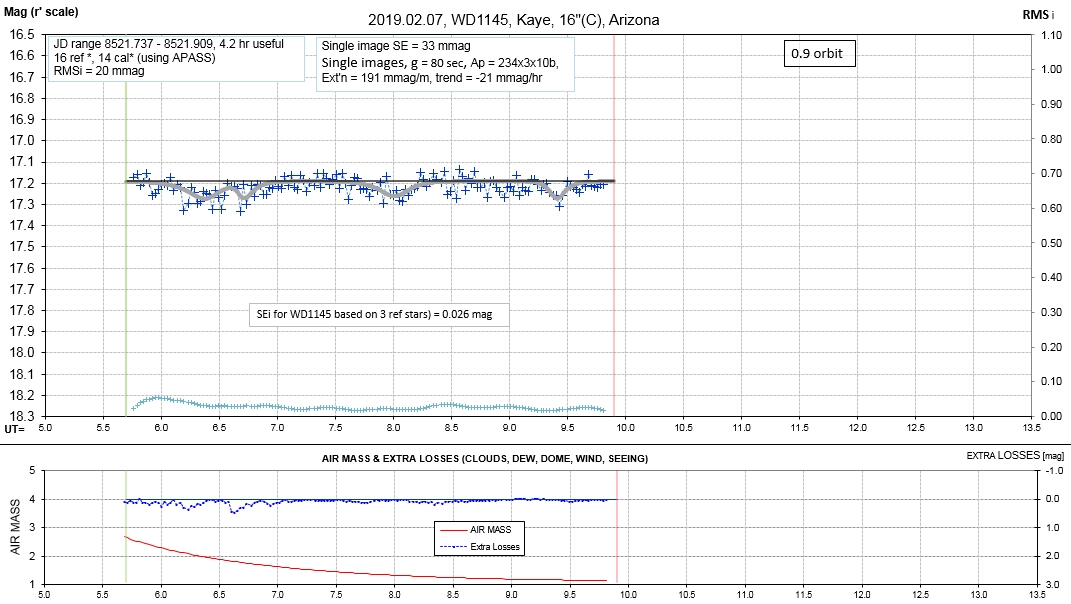
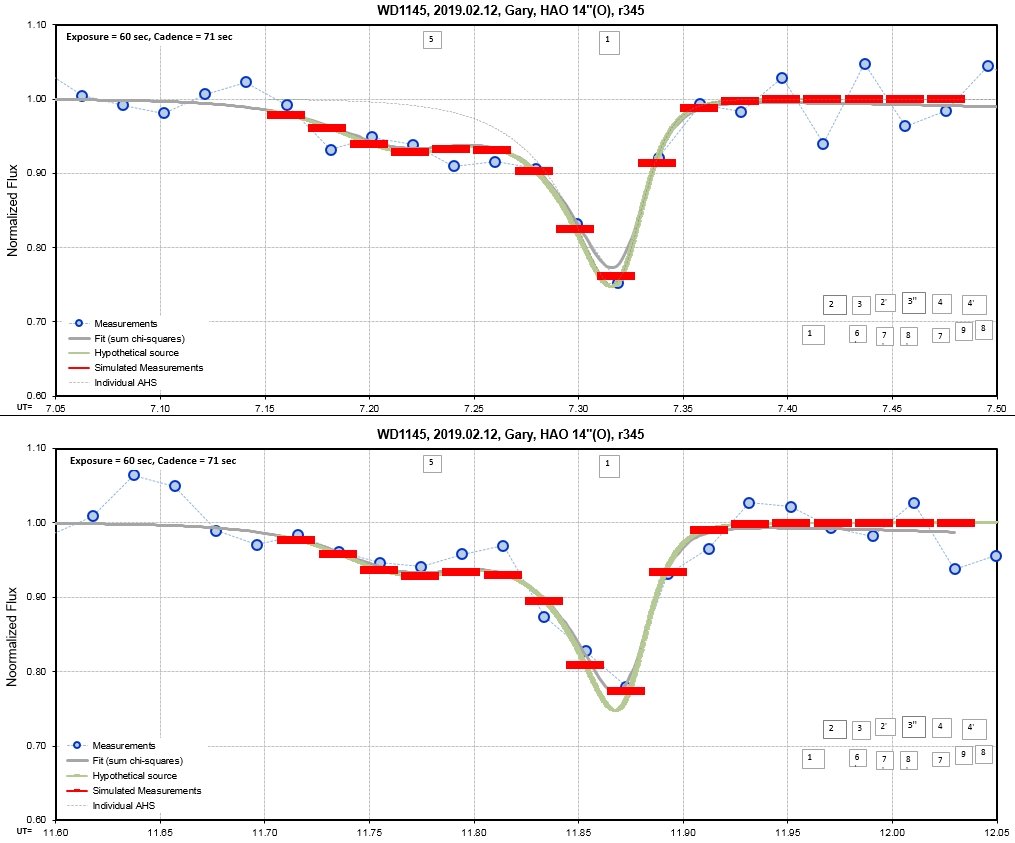
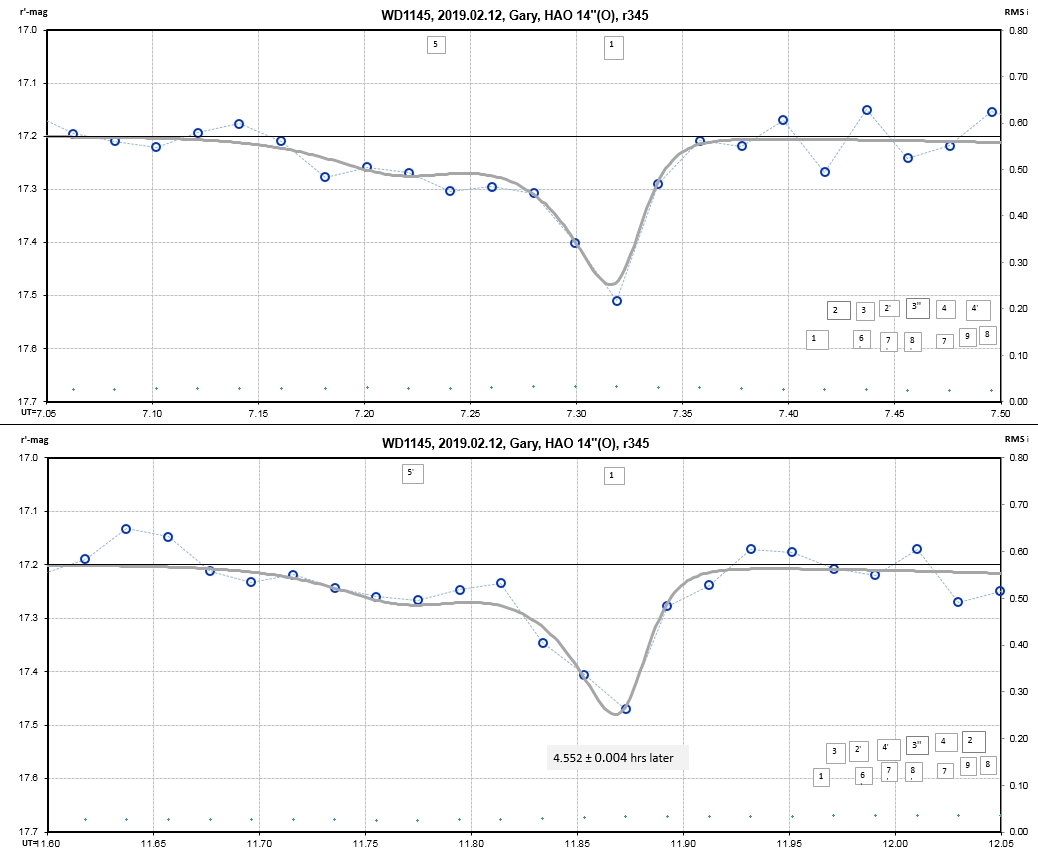
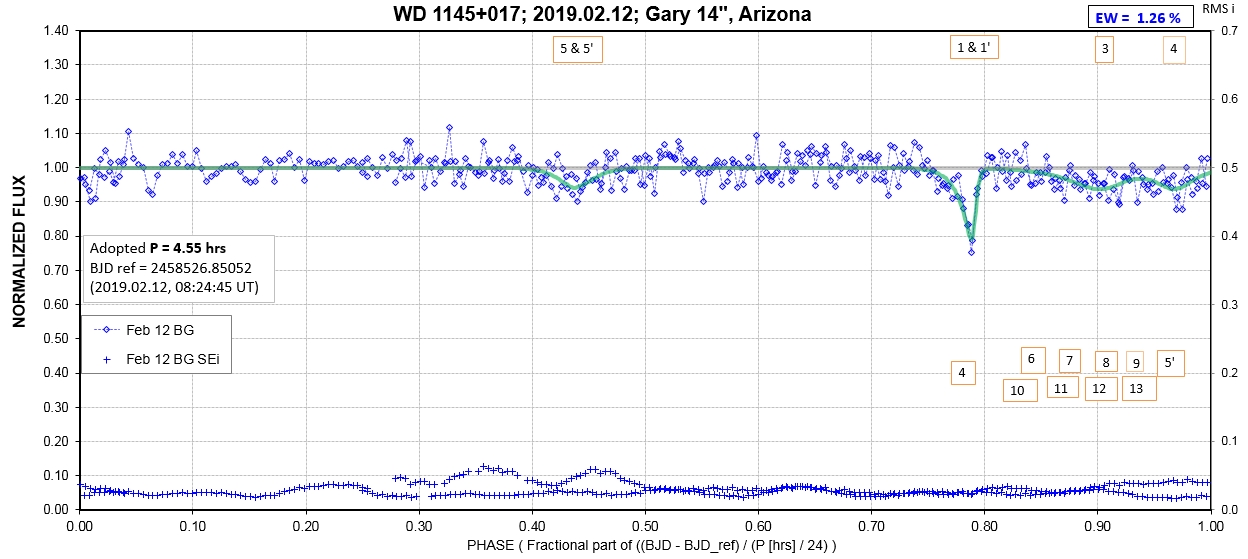
6. White Dwarf WD 1145+017 Photometric Monitoring Observations by Amateur Observers B. Gary & T. Kaye
B. L. Gary, this is the 6th of 6 web pages. Last updated 2020.01.20 05 UT

1 of 7 - 2015.11.01 to 2016.01.21:  LC Observations  - 1st  set of LCs, for 2015/16 observing season   
2 of 7 - 2016.01.17 to 2016.07.13:  LC Observations  - 2nd set of LCs, for 2015/16 observing season    
3 of 7 - 2015.11.01 to 2016.07.13:  LC Observations  - 3rd set of LCs, for 2015/16 observing season  (N = 158) + Overview, Results & Model Speculations 
4 of 7 - 2016.10.25 to 2017.06.18:  LC Observations  - 4th set of LCs, for 2016/17 observing season 
5 of 7 - 2017.10.23 to 2018.06.18:  LC Observations  - 5th set of LCs, for 2017/18 observing season 
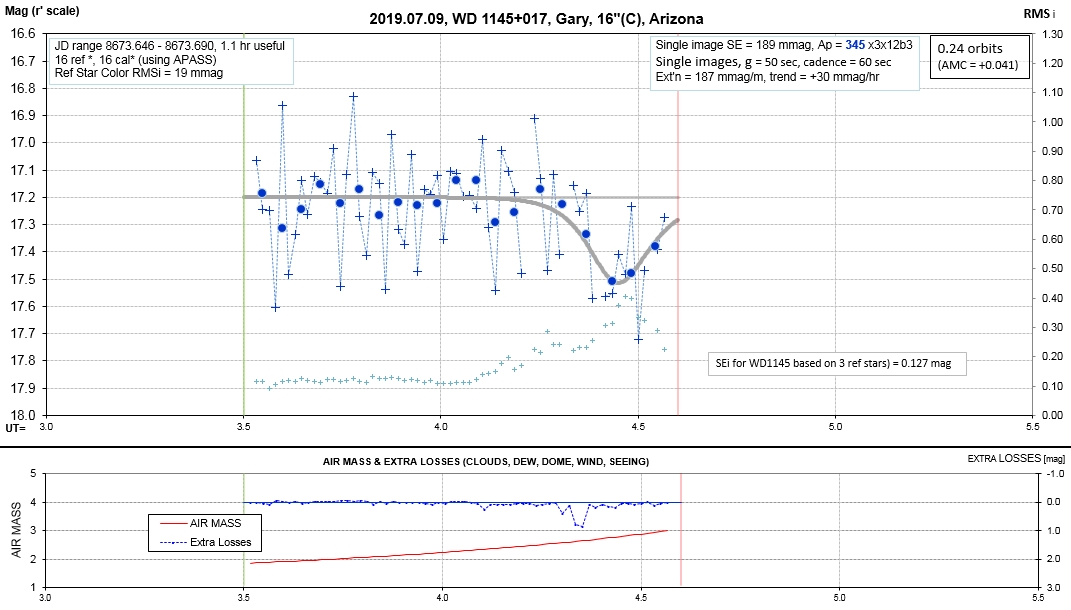
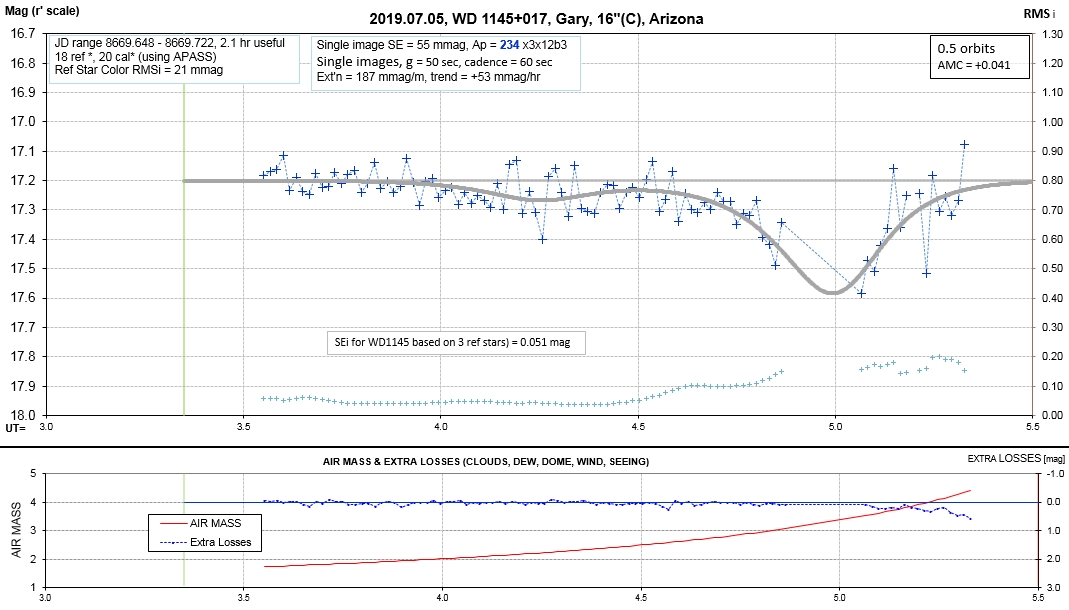
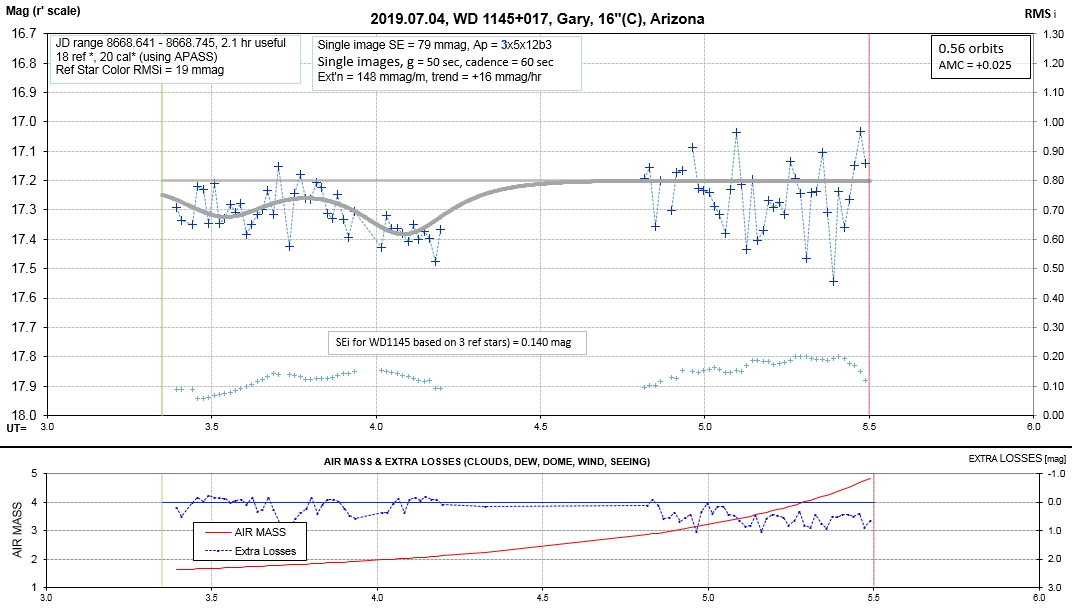
6 of 7 - 2018.11.06 to 2018.07.09   LC Observations  - 6th set of LCs, for 2018/19 observing season   (YOU ARE HERE)
Previous 4 observing seasons:        Observational findings that need to be explained by models  
7 of 7 - 2019.12.02 to present         LC Observations - 7th set of LCs, for 2019/20 observing season 

Links on this web page:
  Status & Summary of Results for this Observing Season  
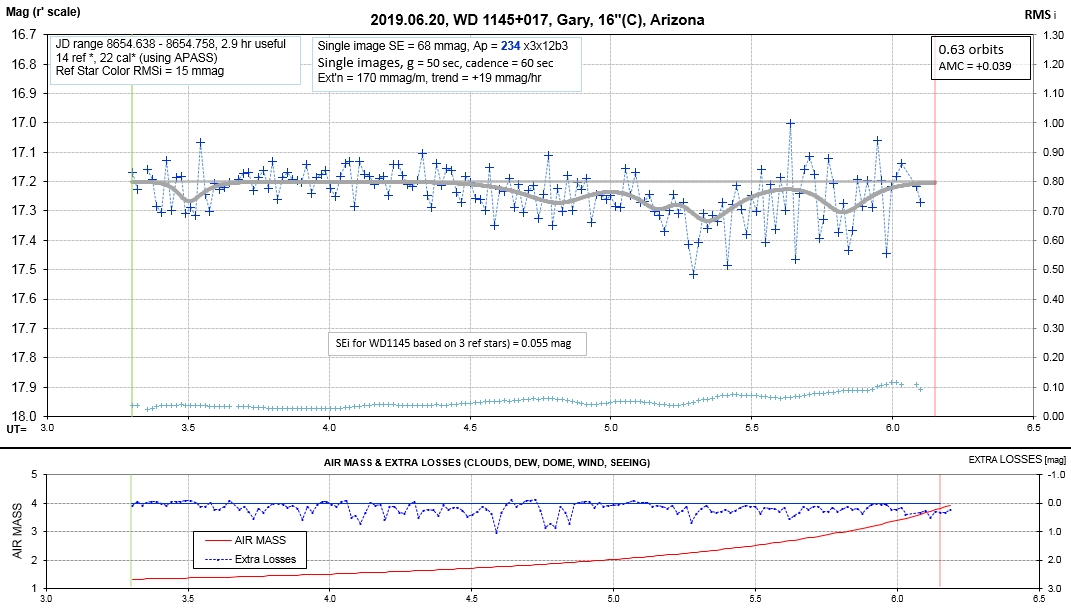
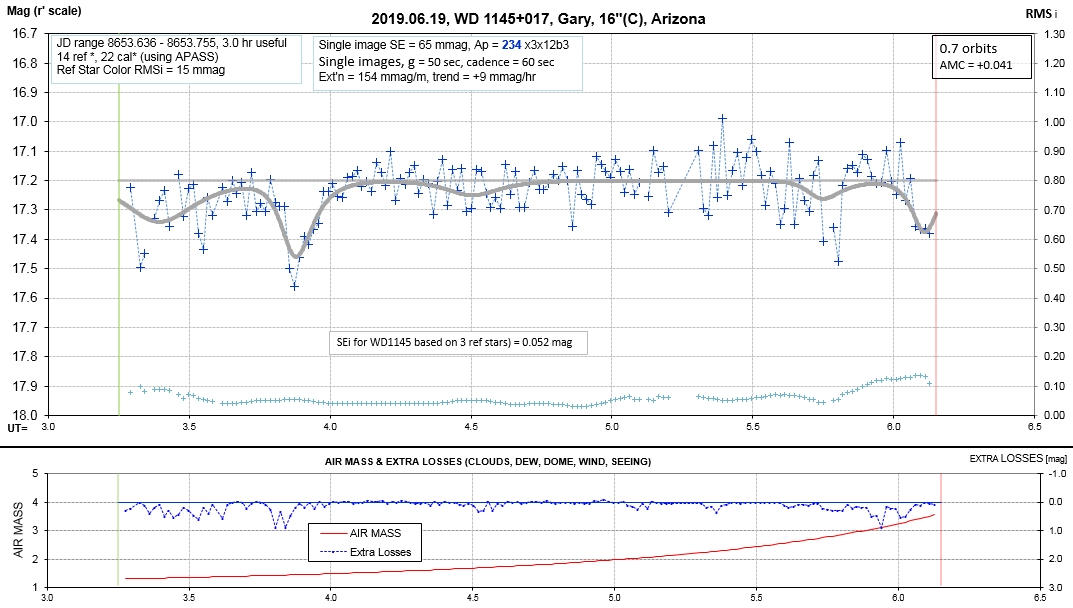
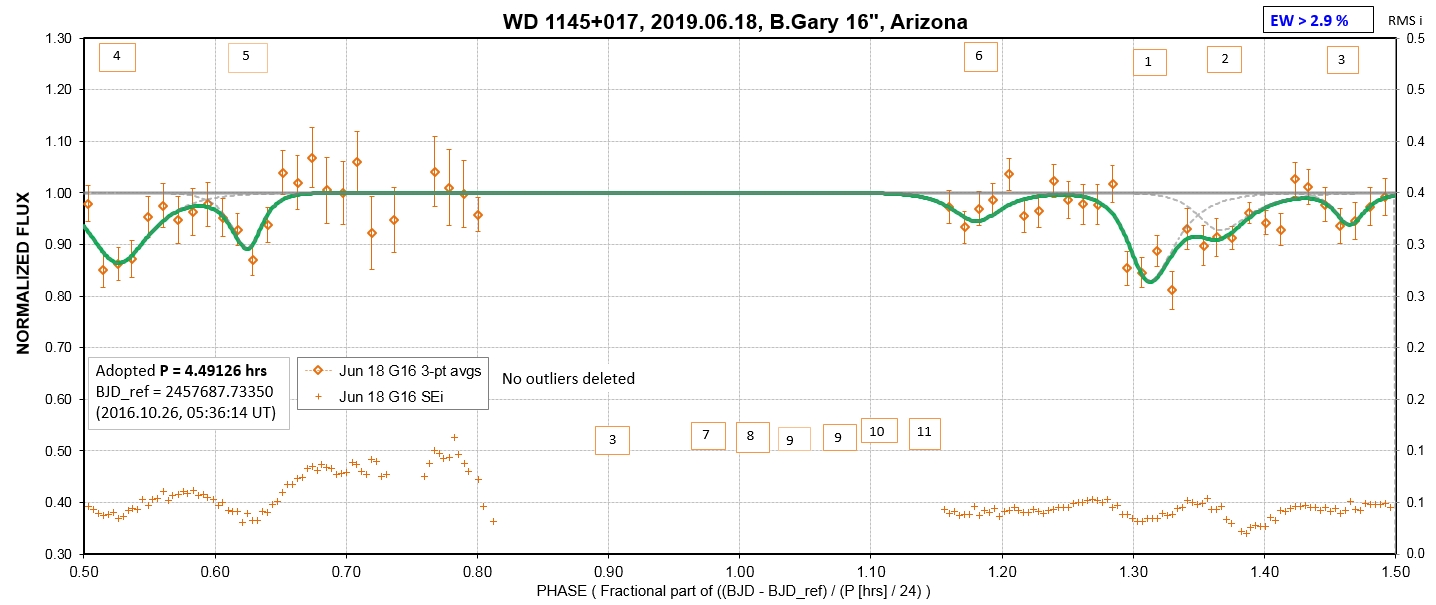
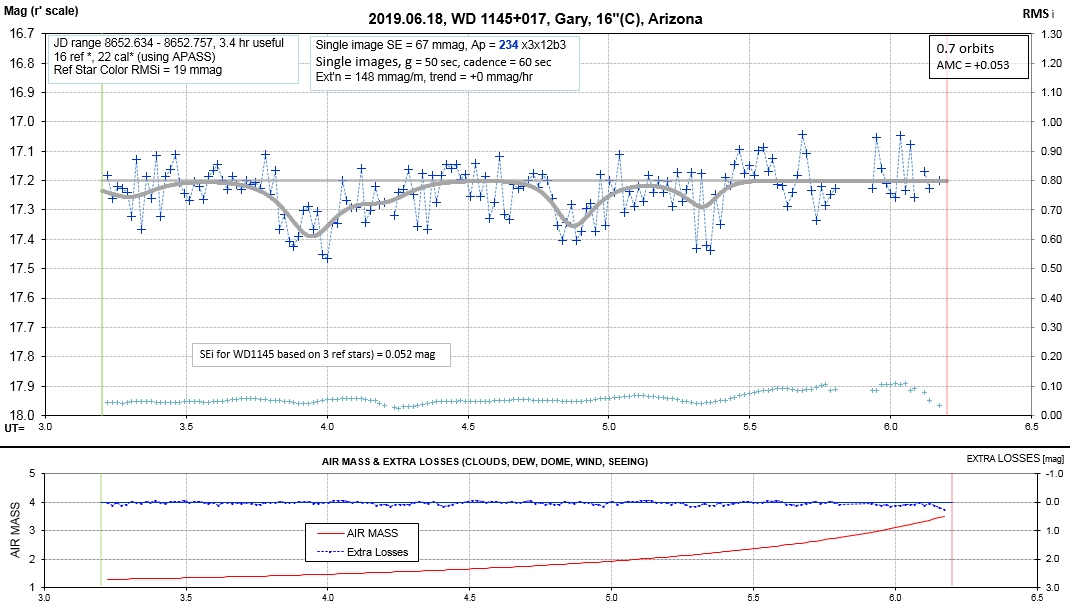
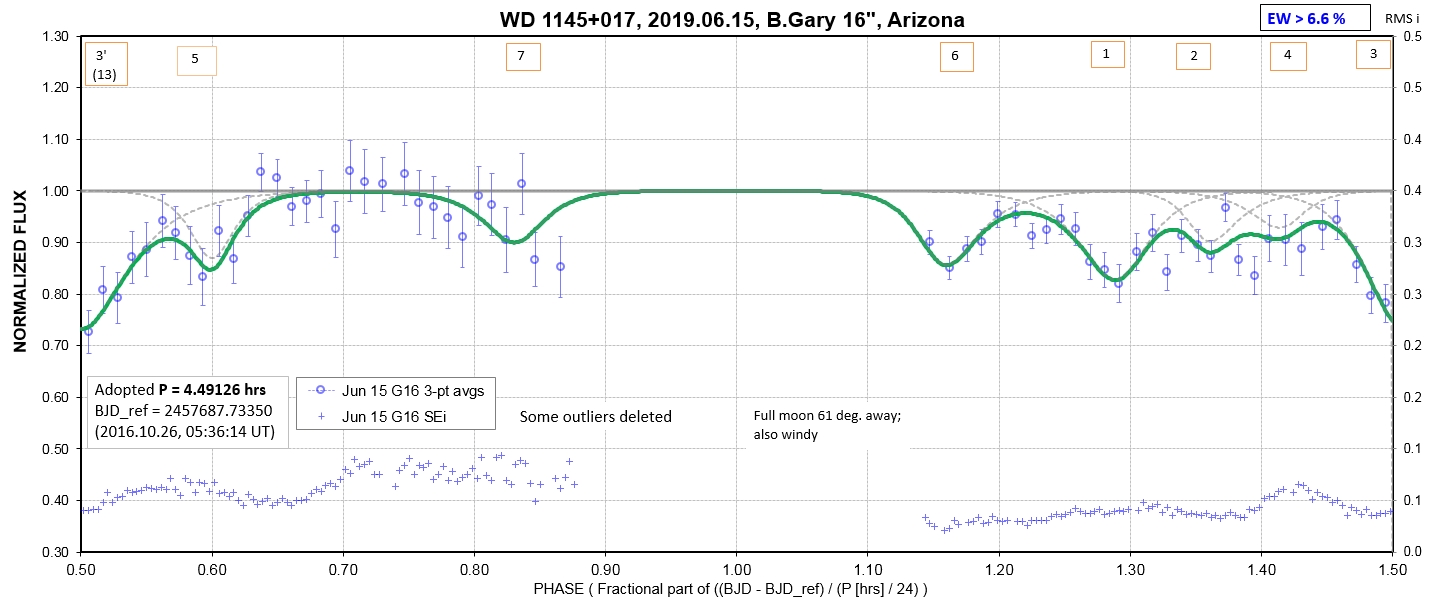
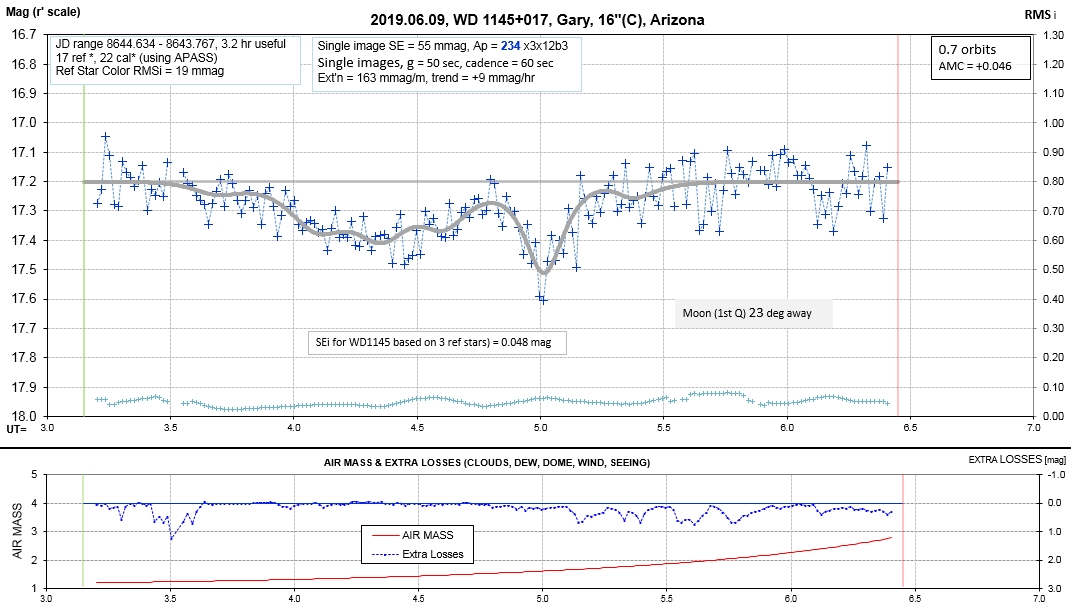
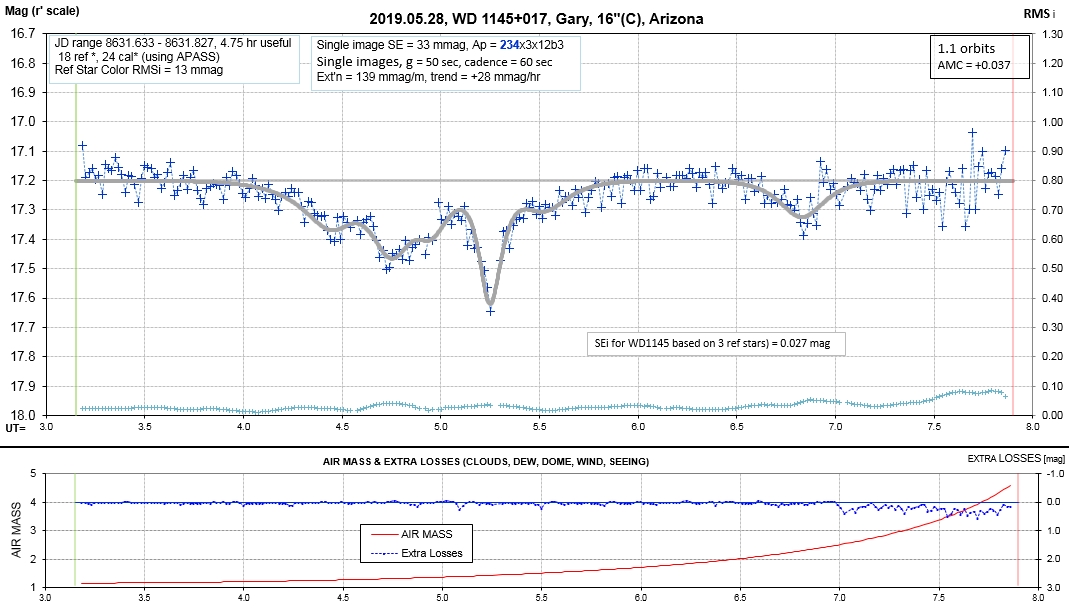
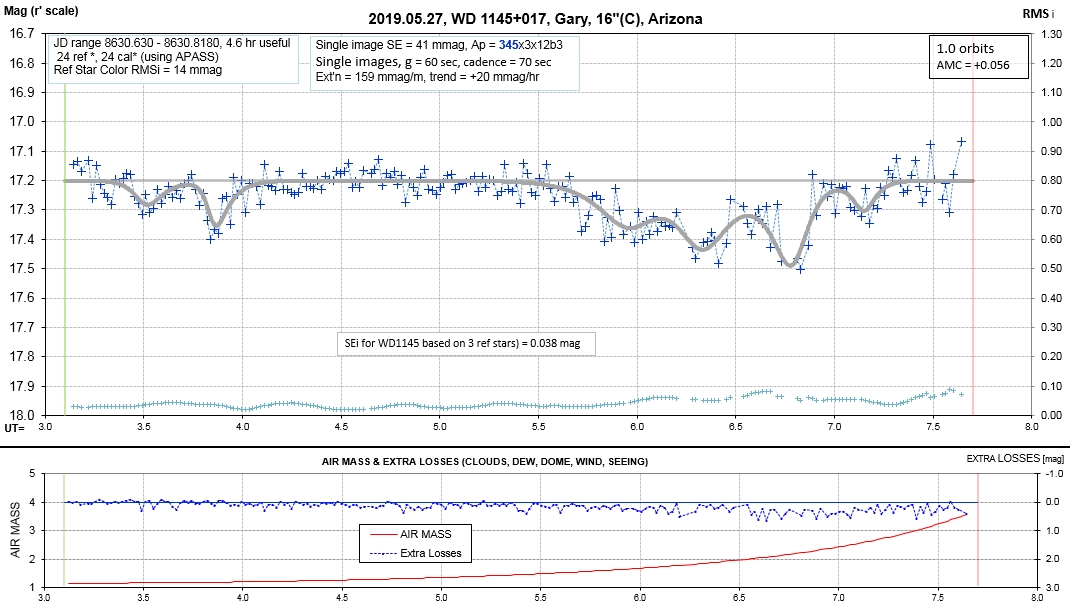
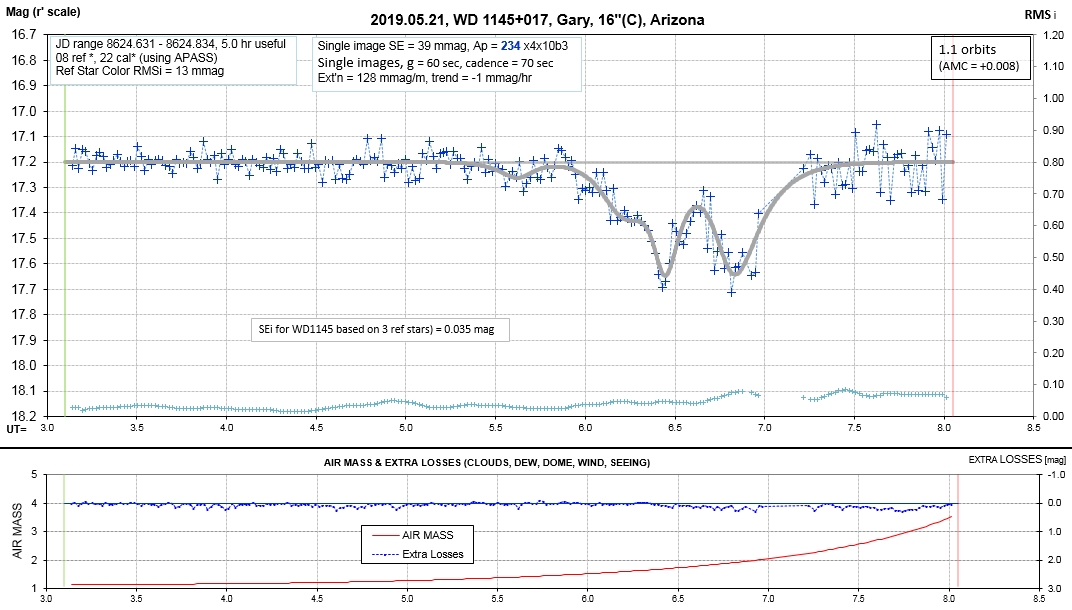
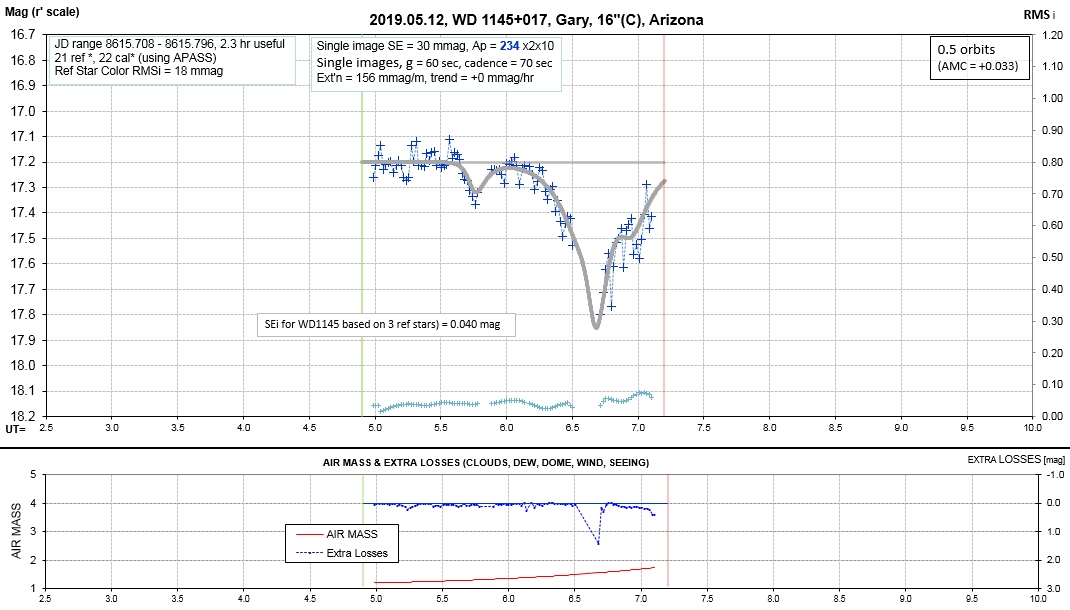
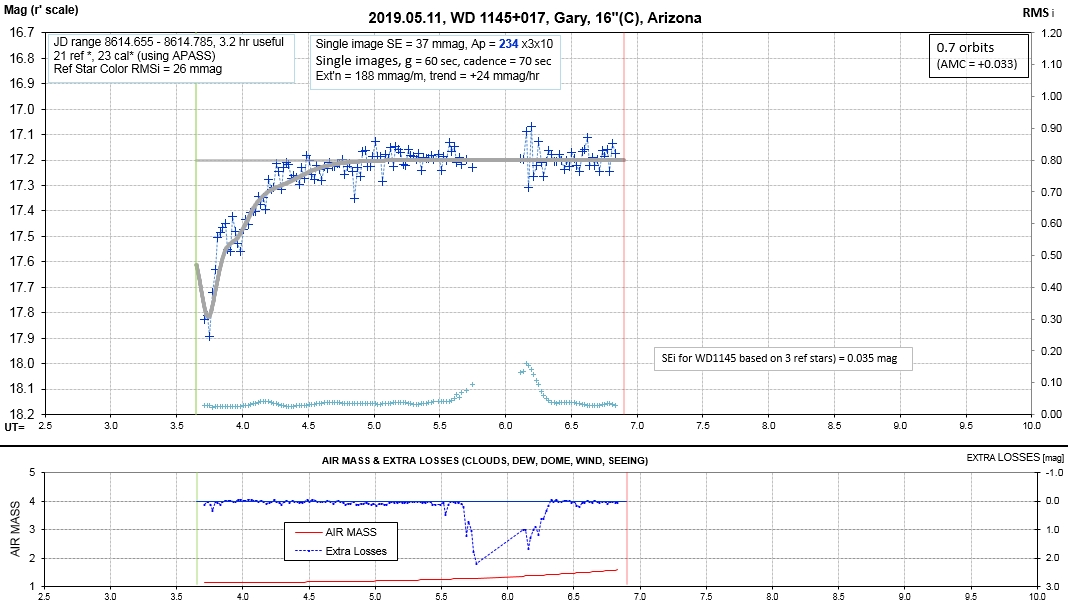
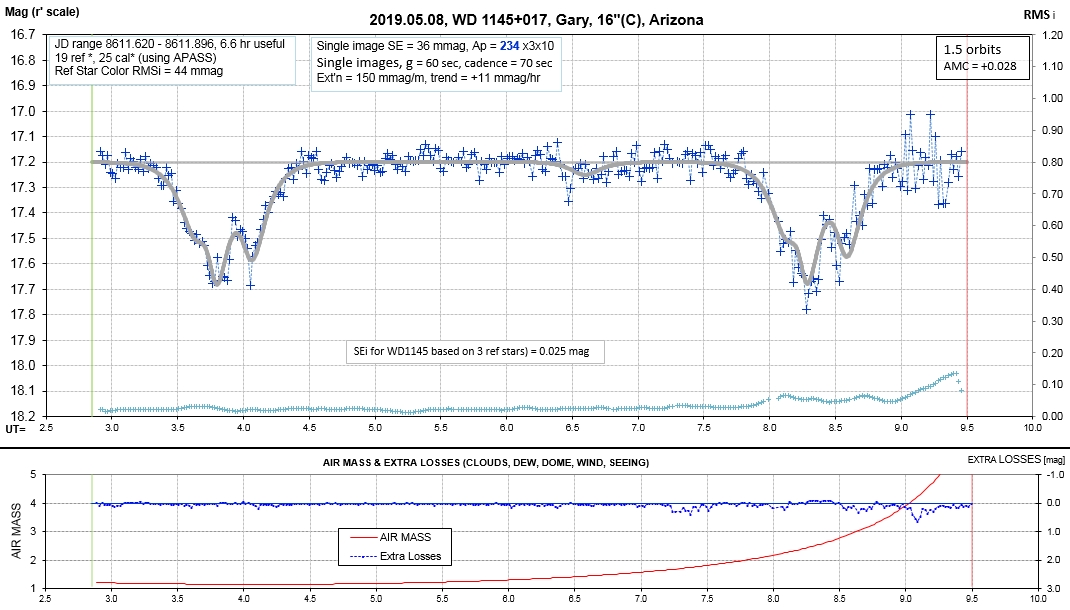
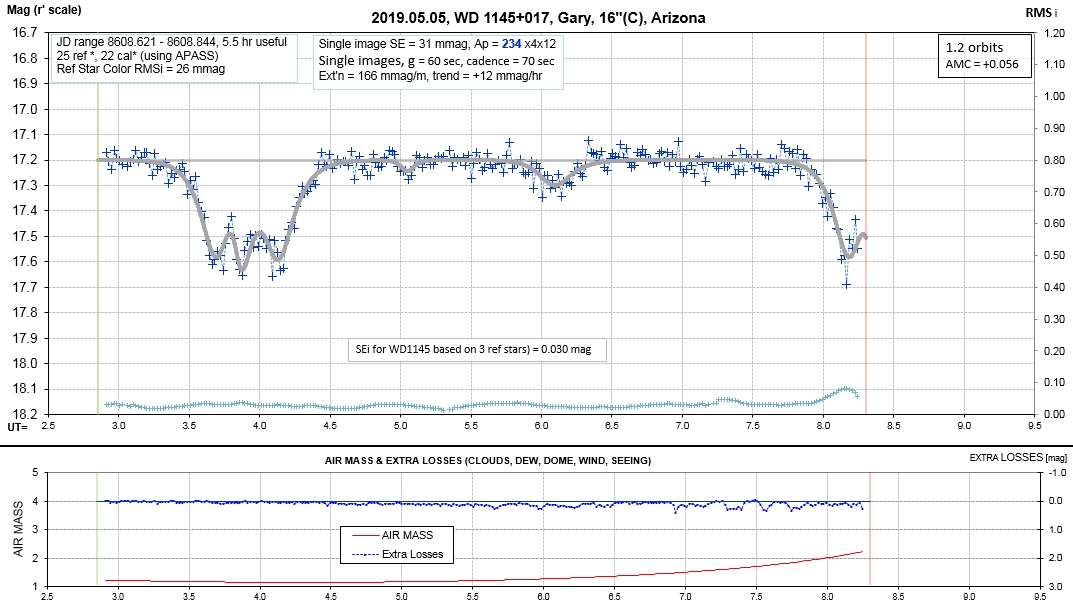
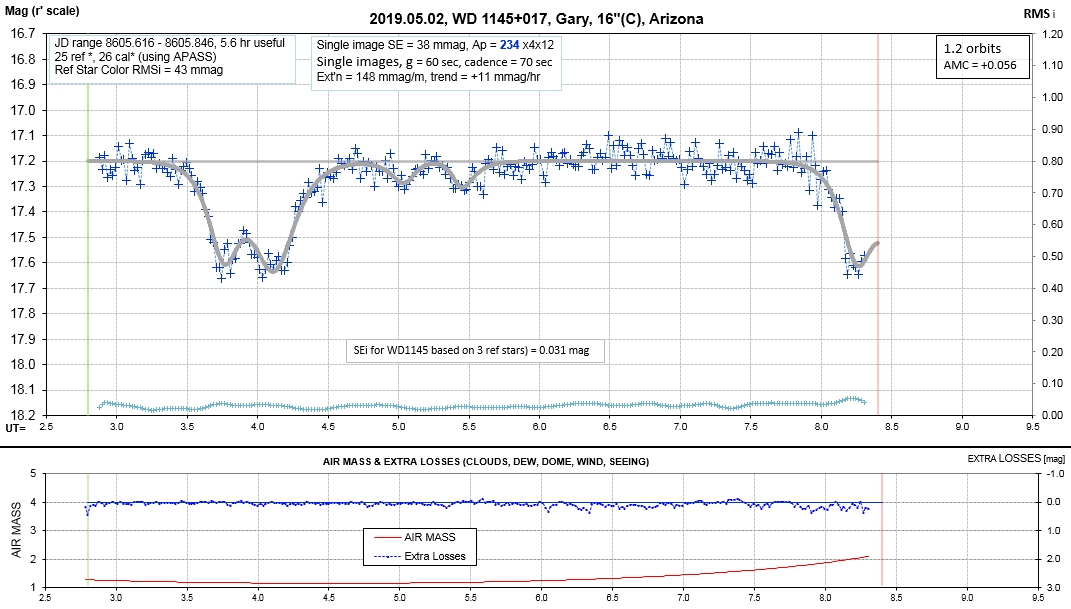
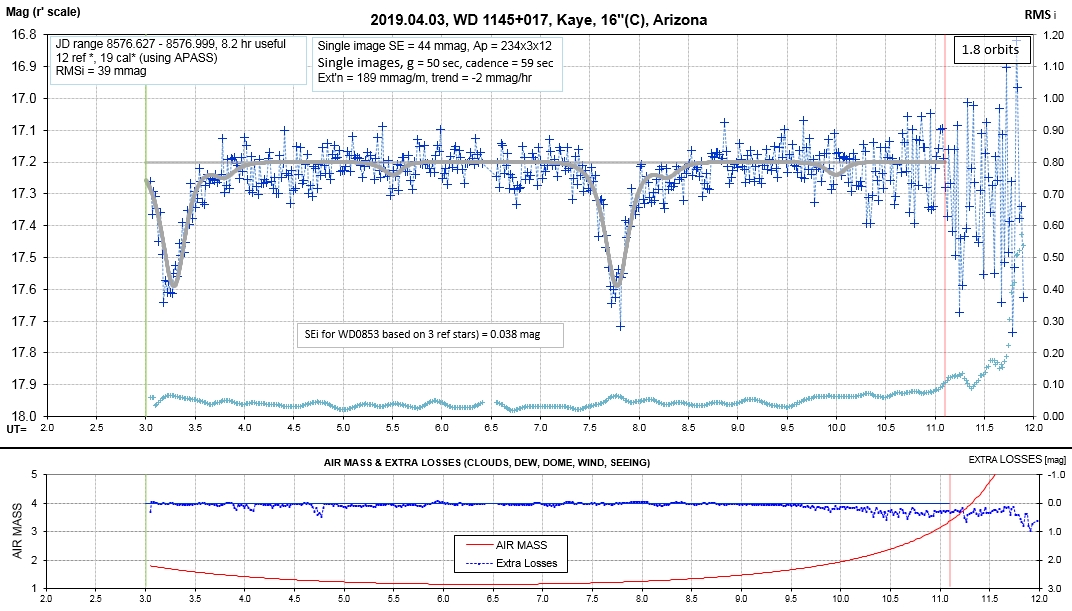
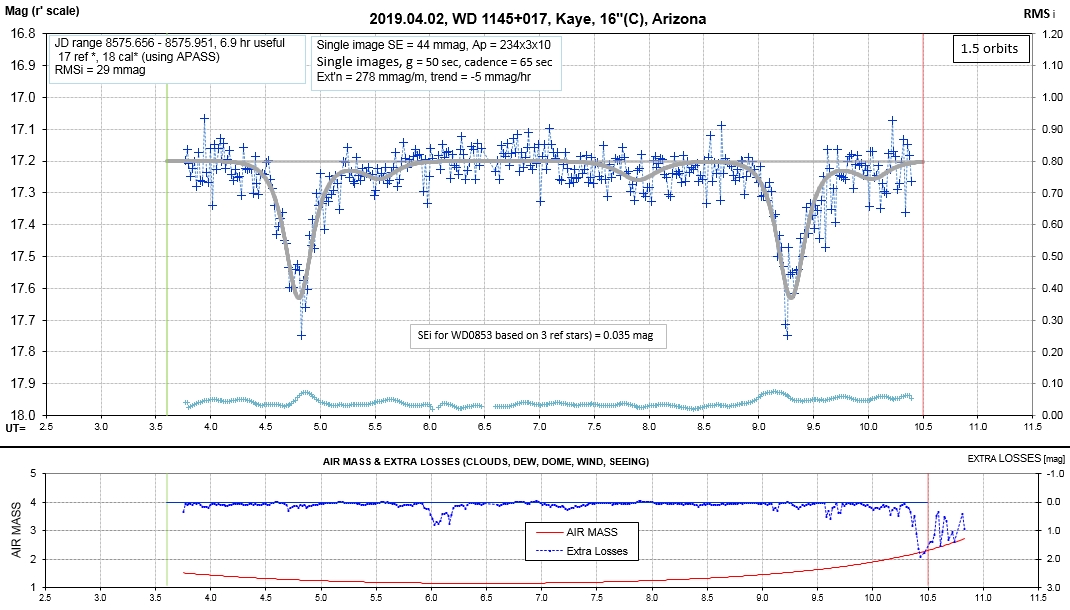
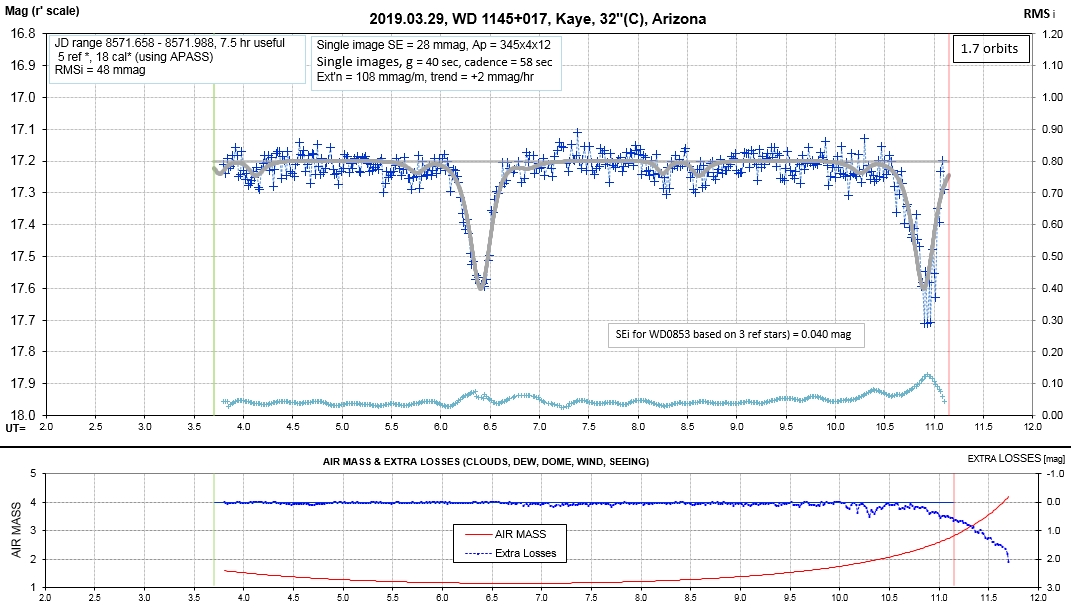
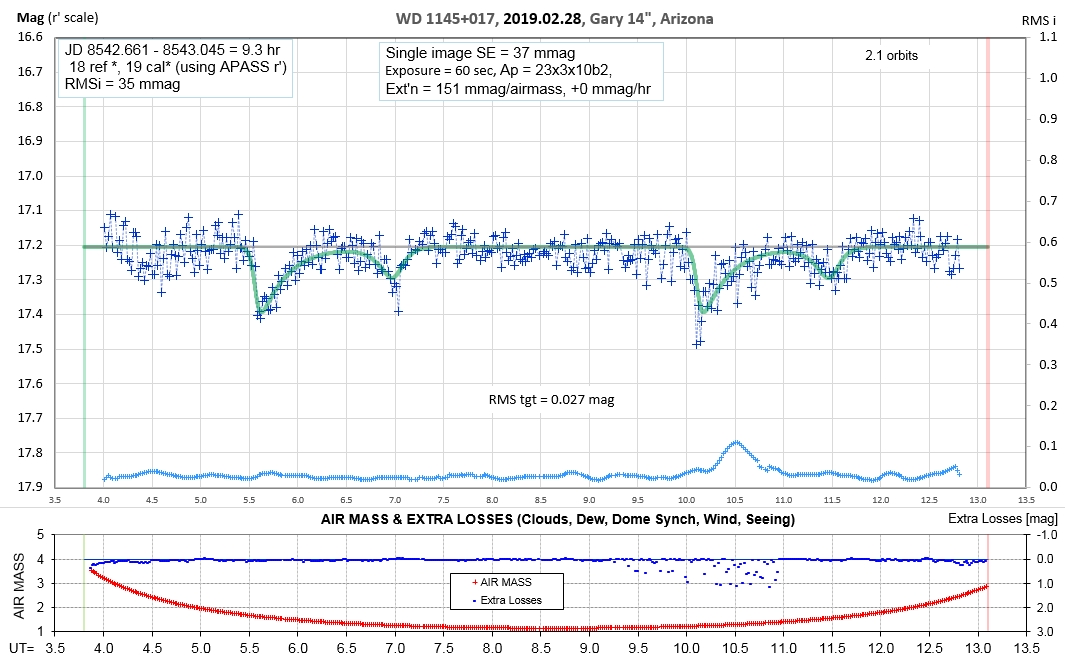
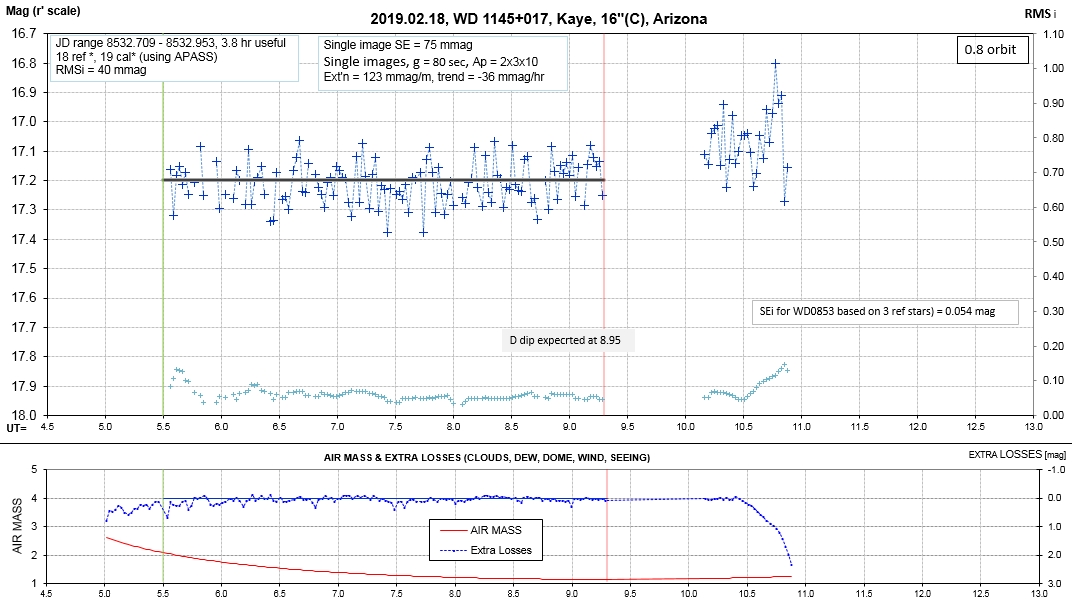
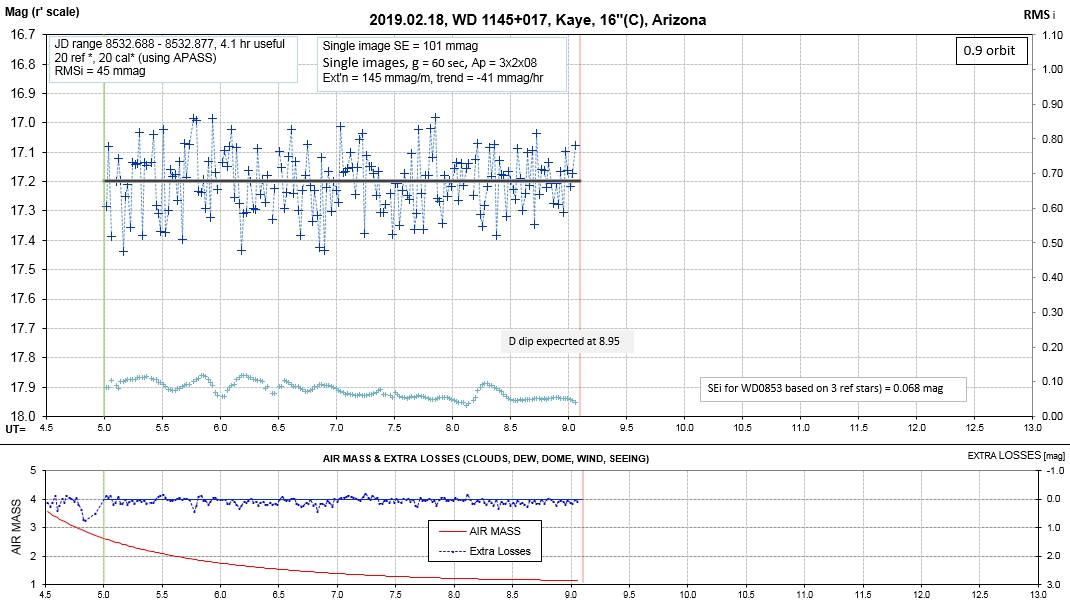
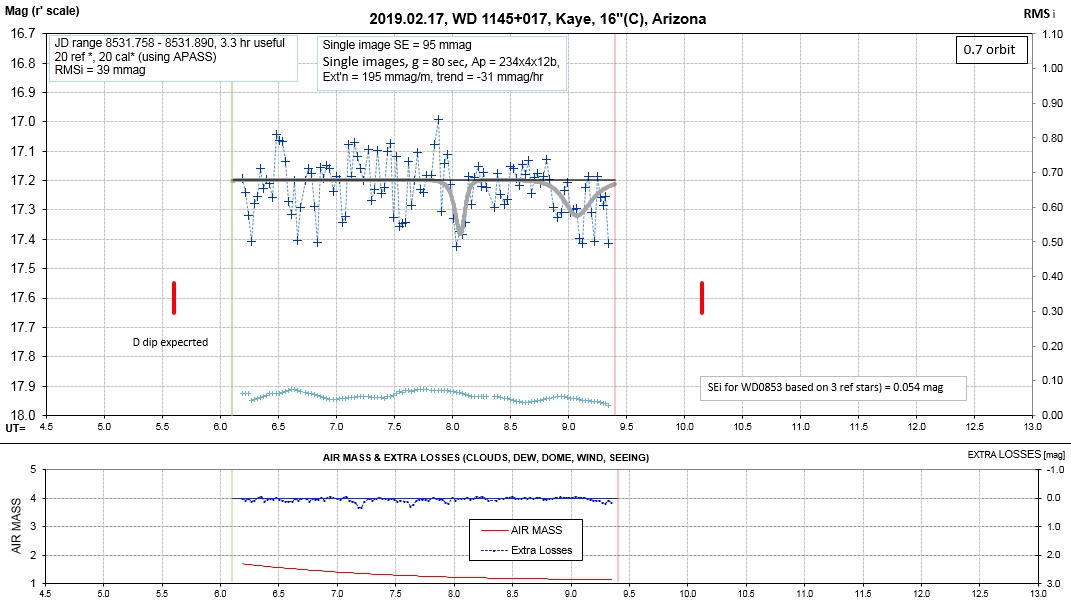
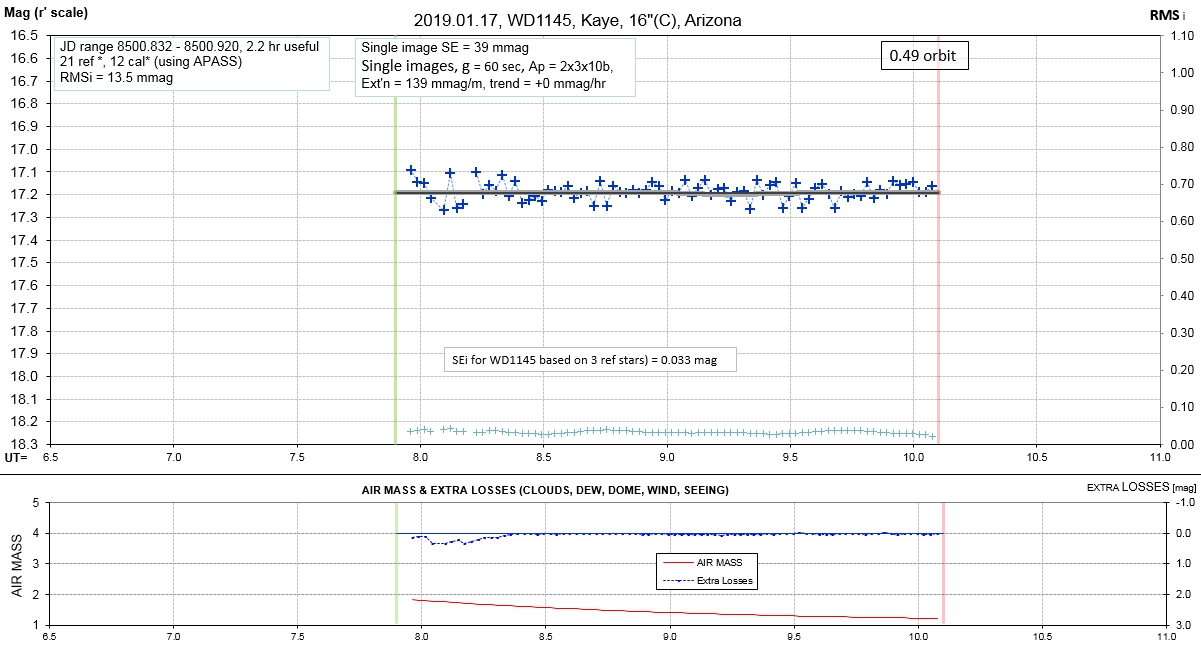
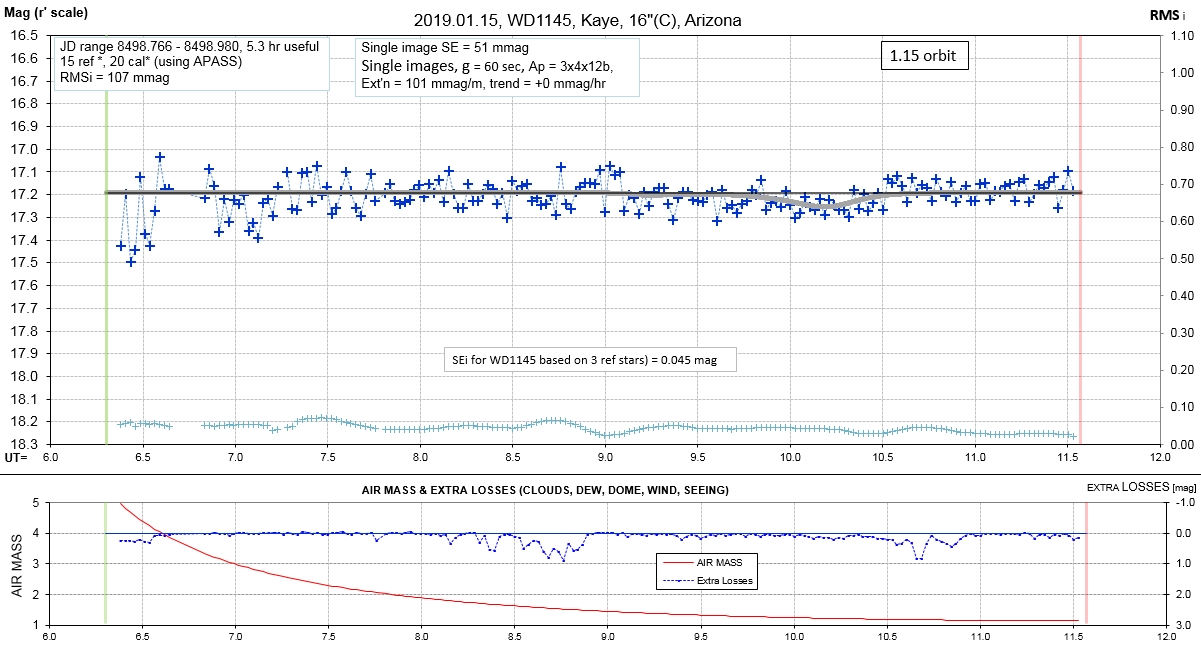
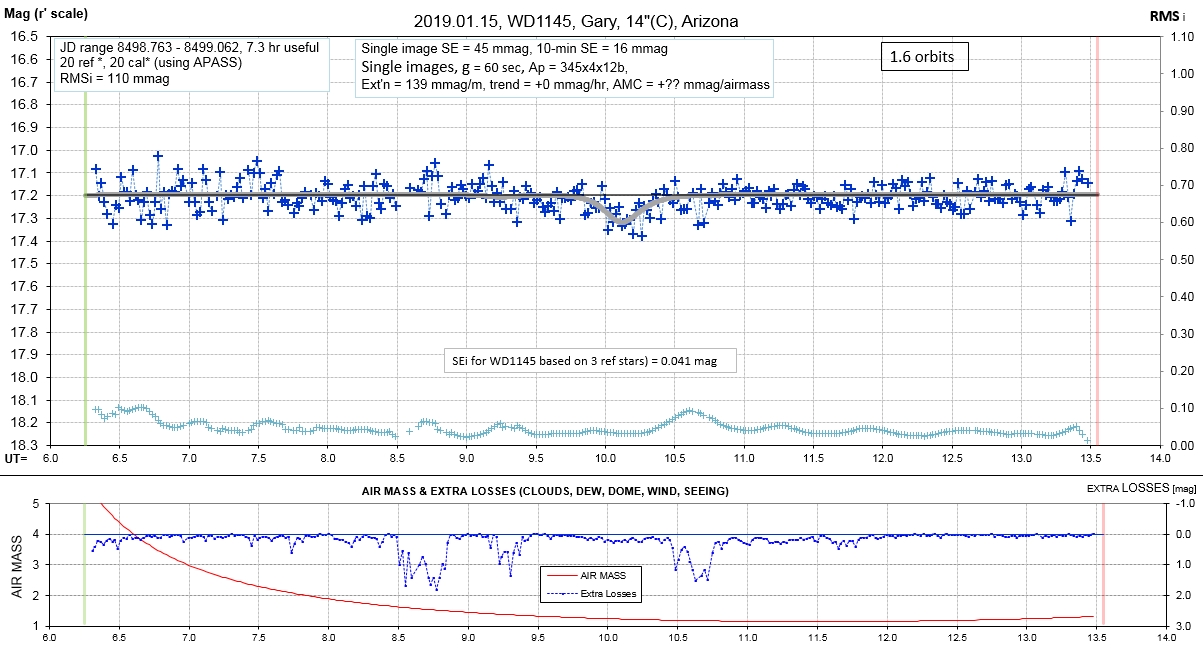
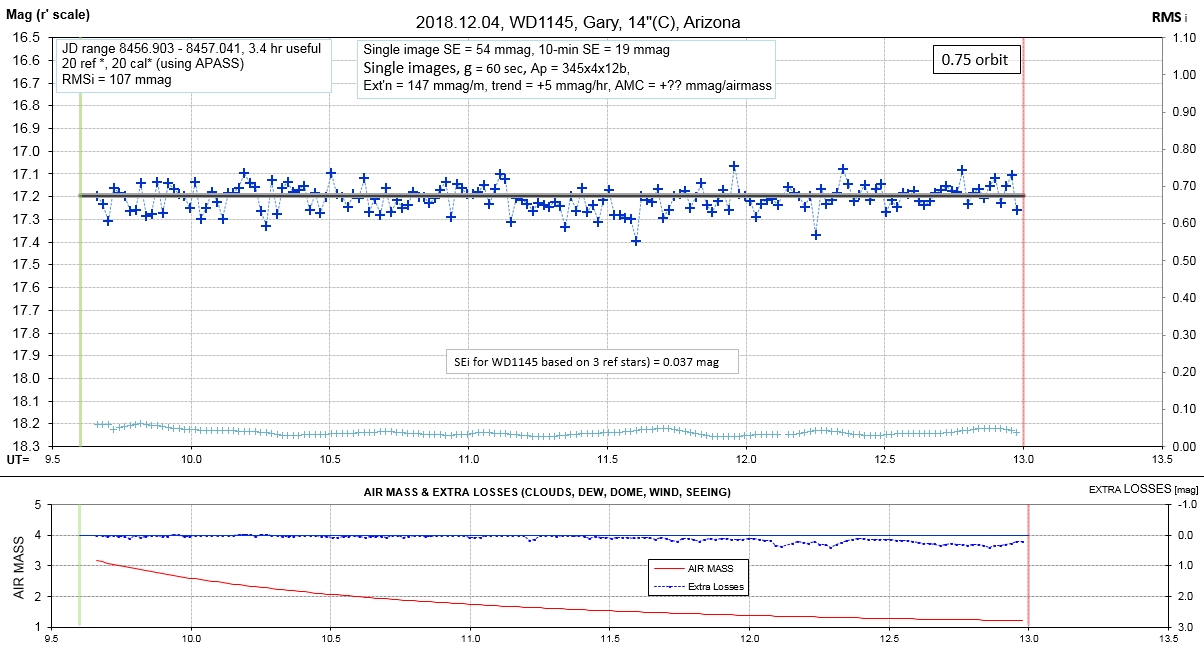
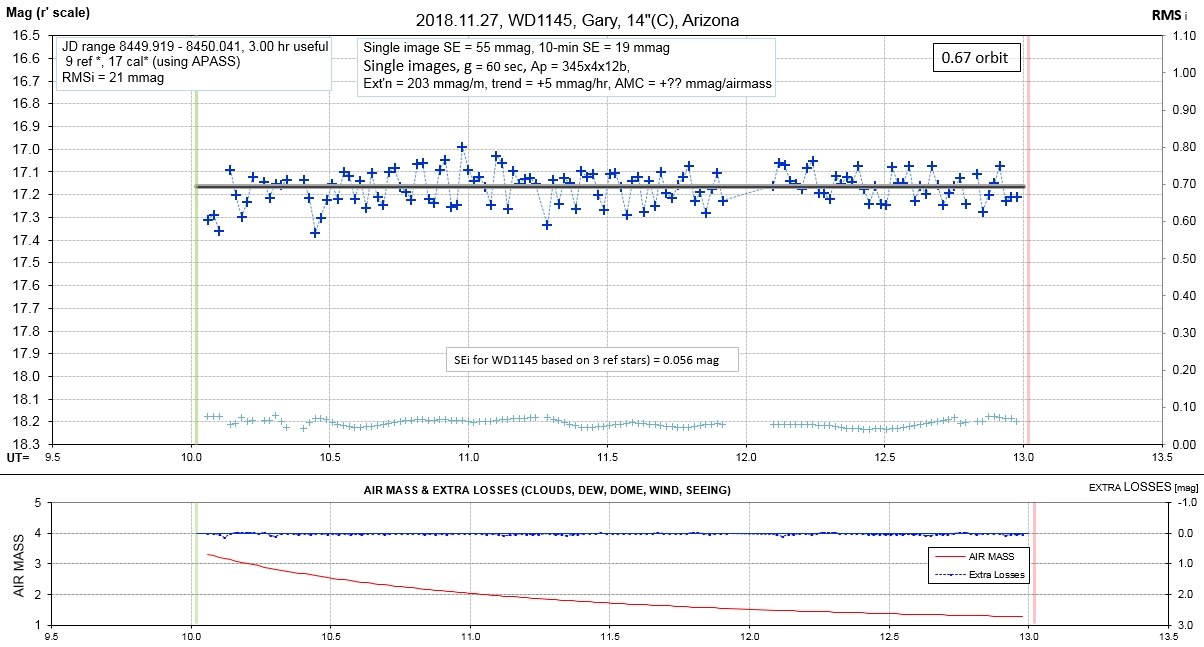
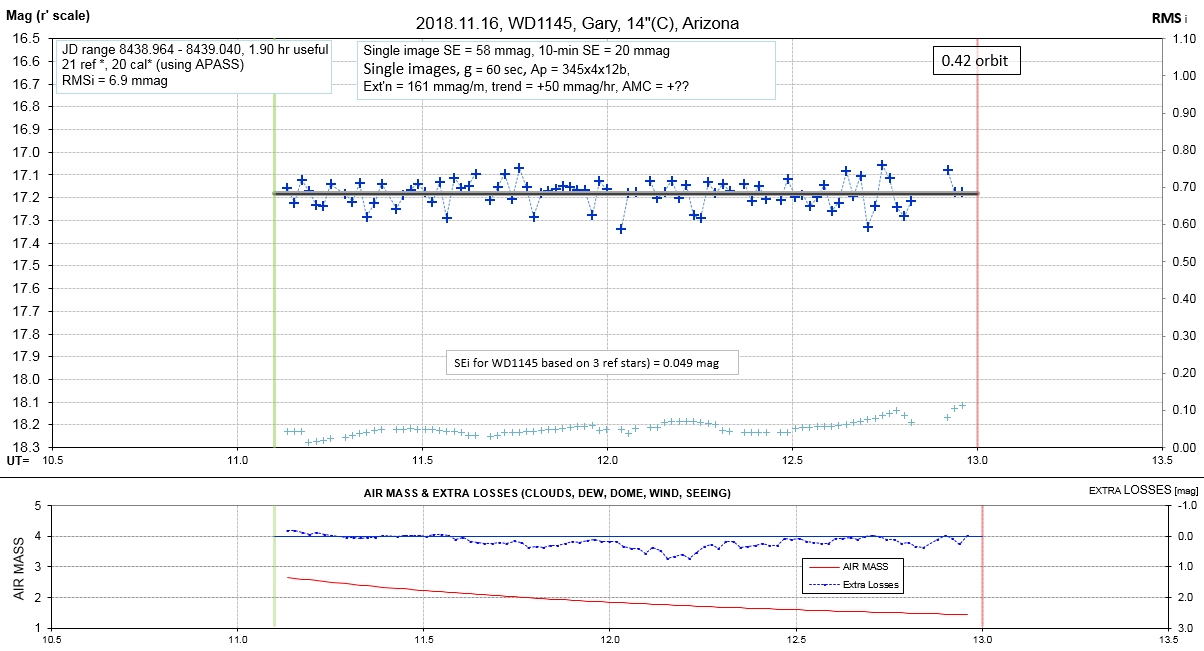
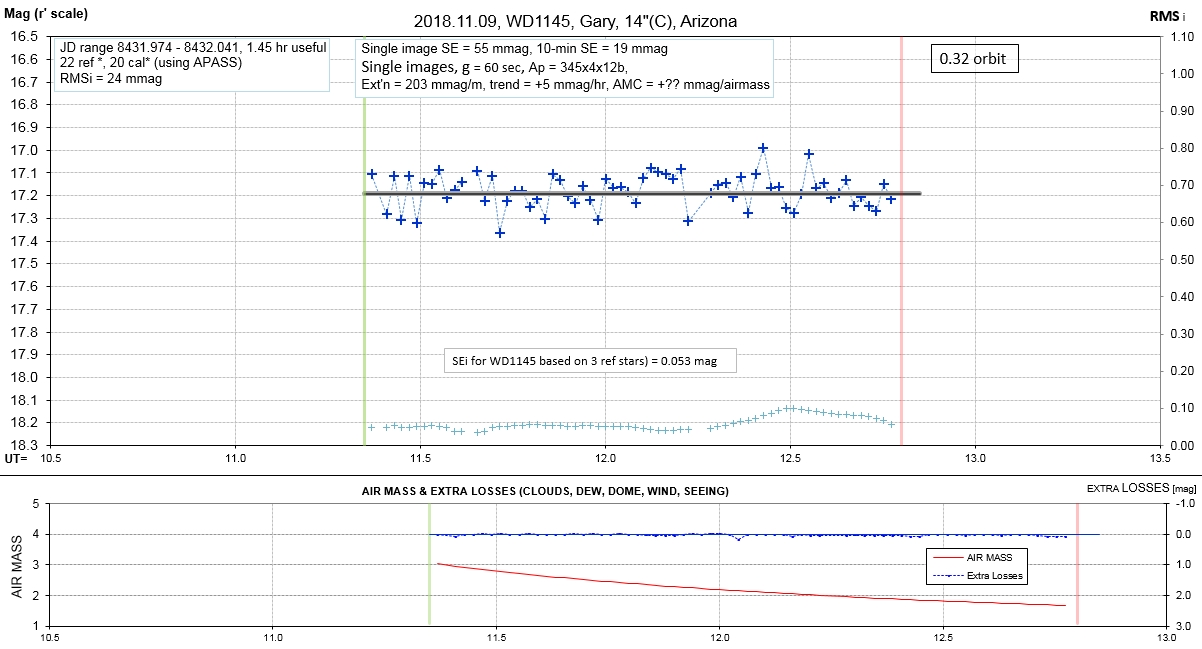
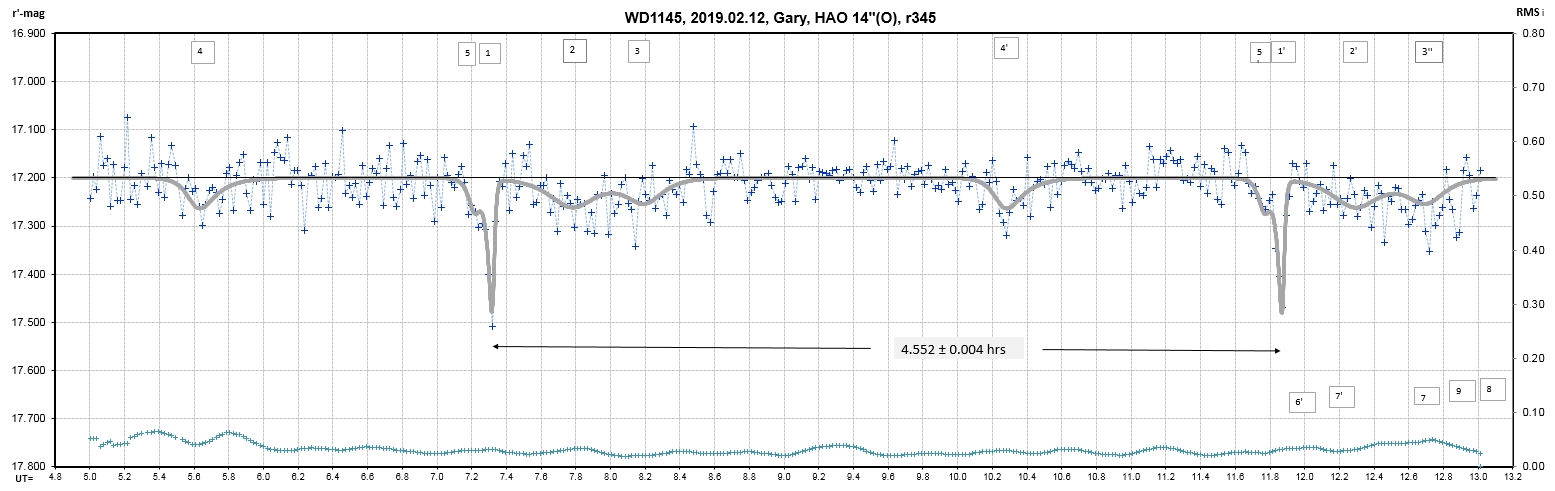
  Observing session LCs 
  Finder image & basic info  
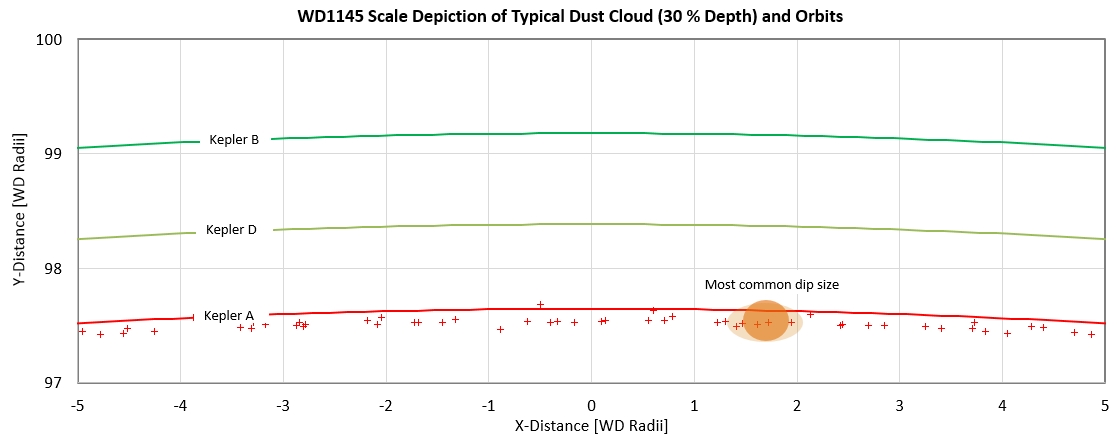
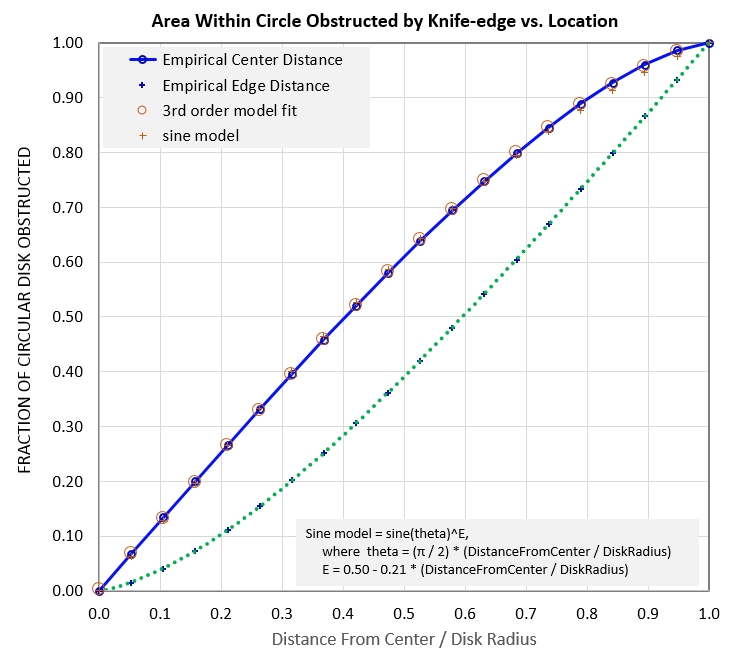
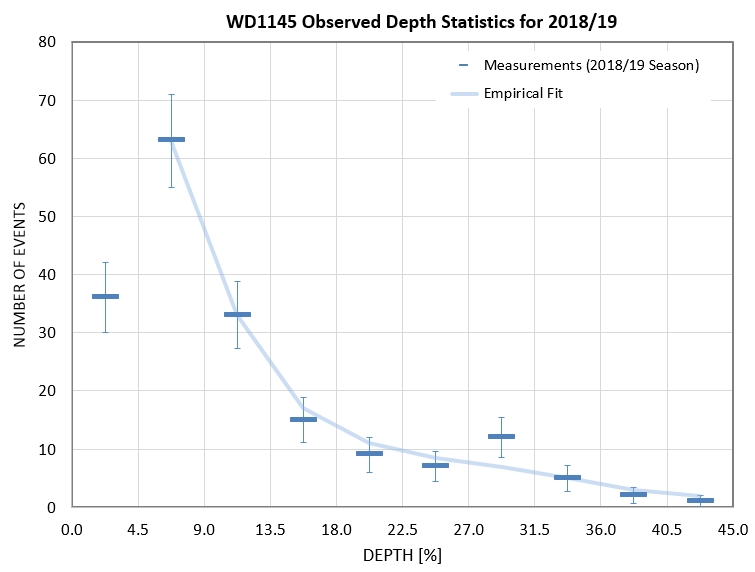
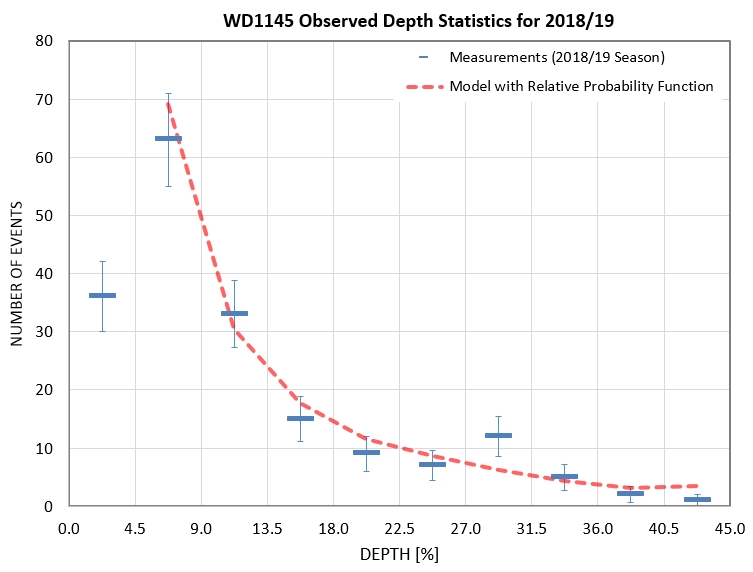
  Miscellaneous analysis and speculation  
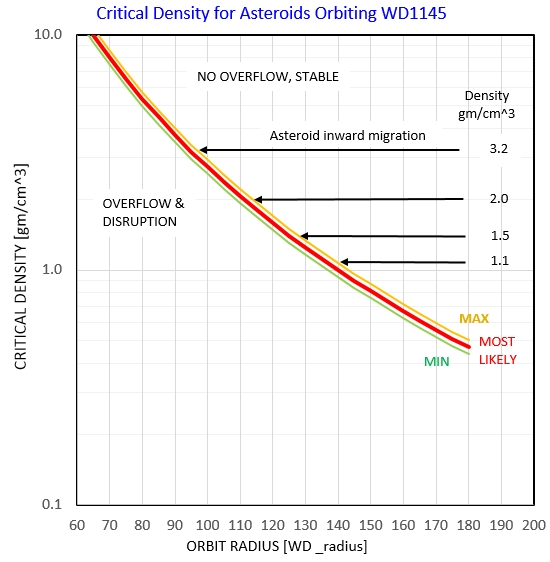
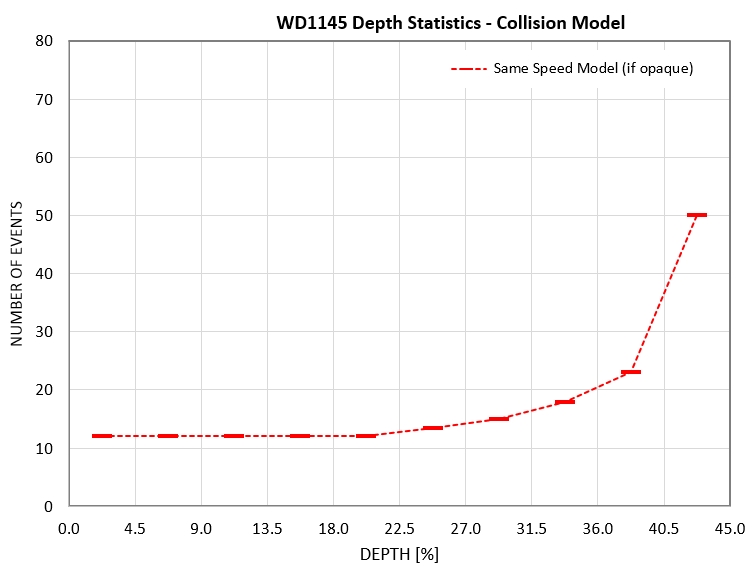
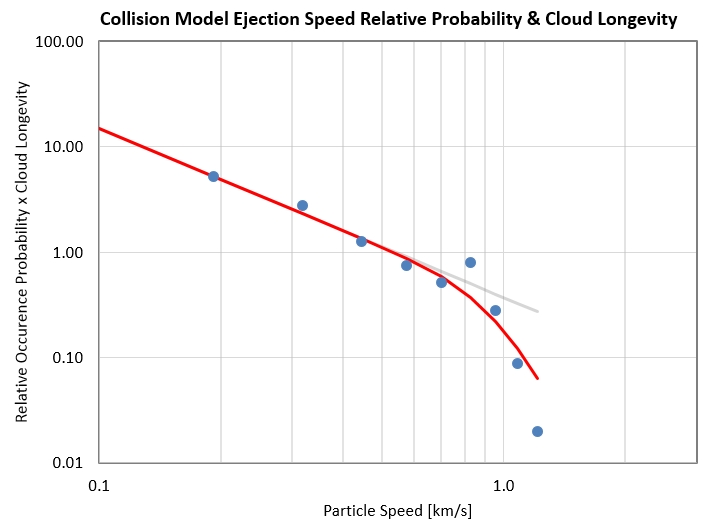
  Collision model thoughts   
  Data exchange files (for all years: 2015/16, 2016/17, etc)
  My collaboration policy 
  References & related external links 

Status & Summary of Results for this Observing Season: 

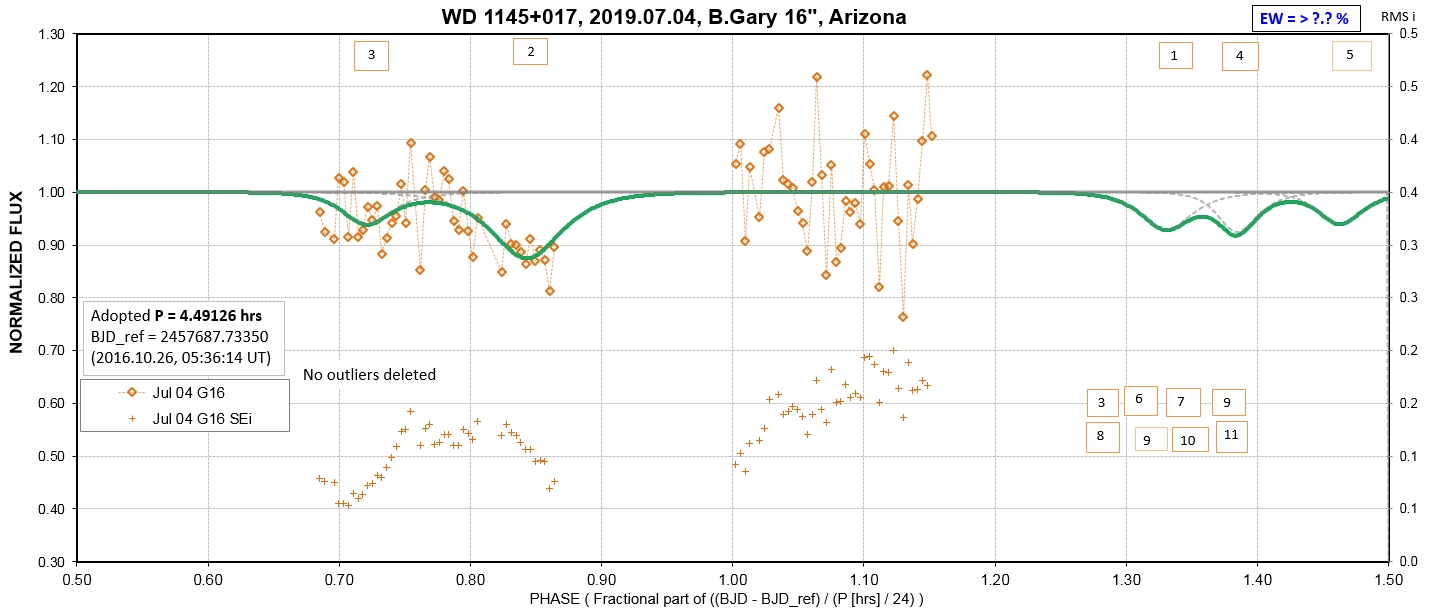
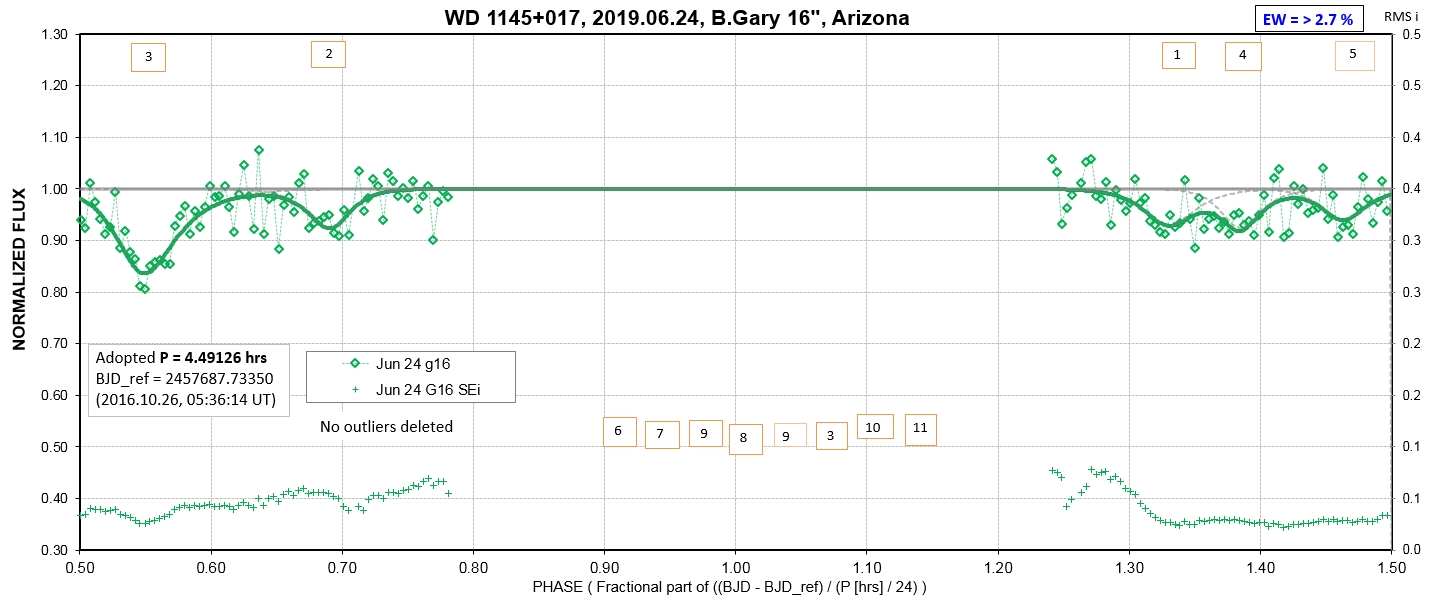
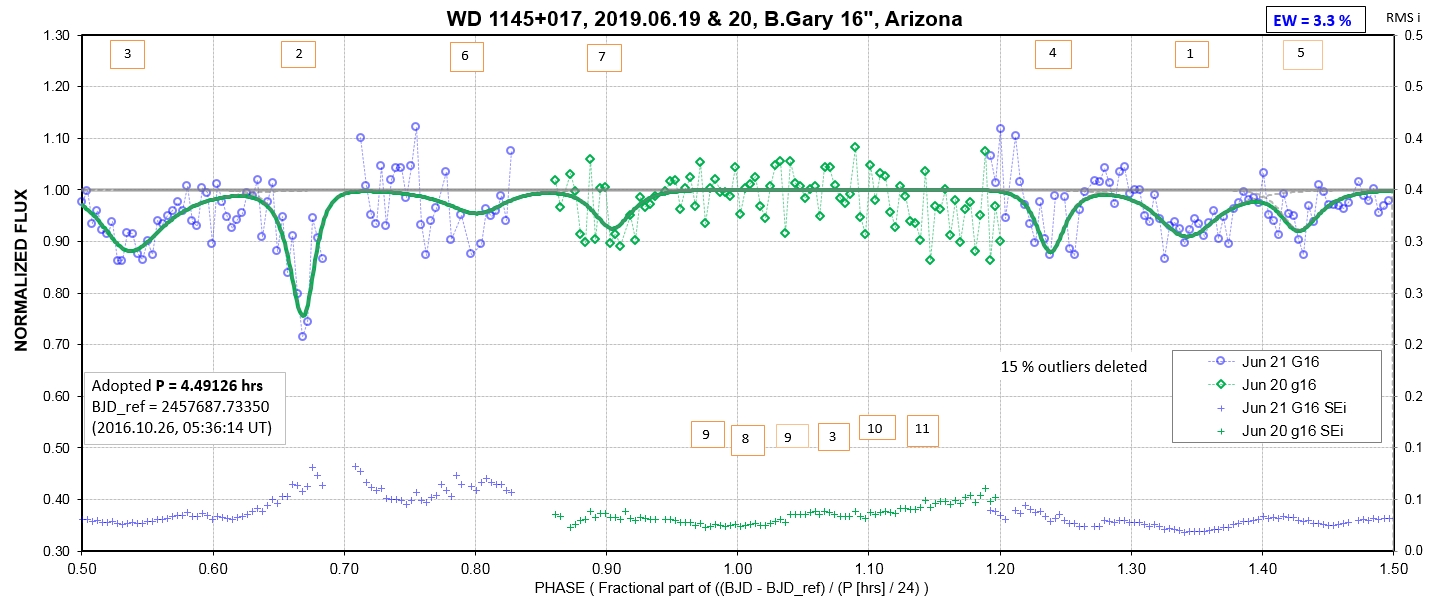
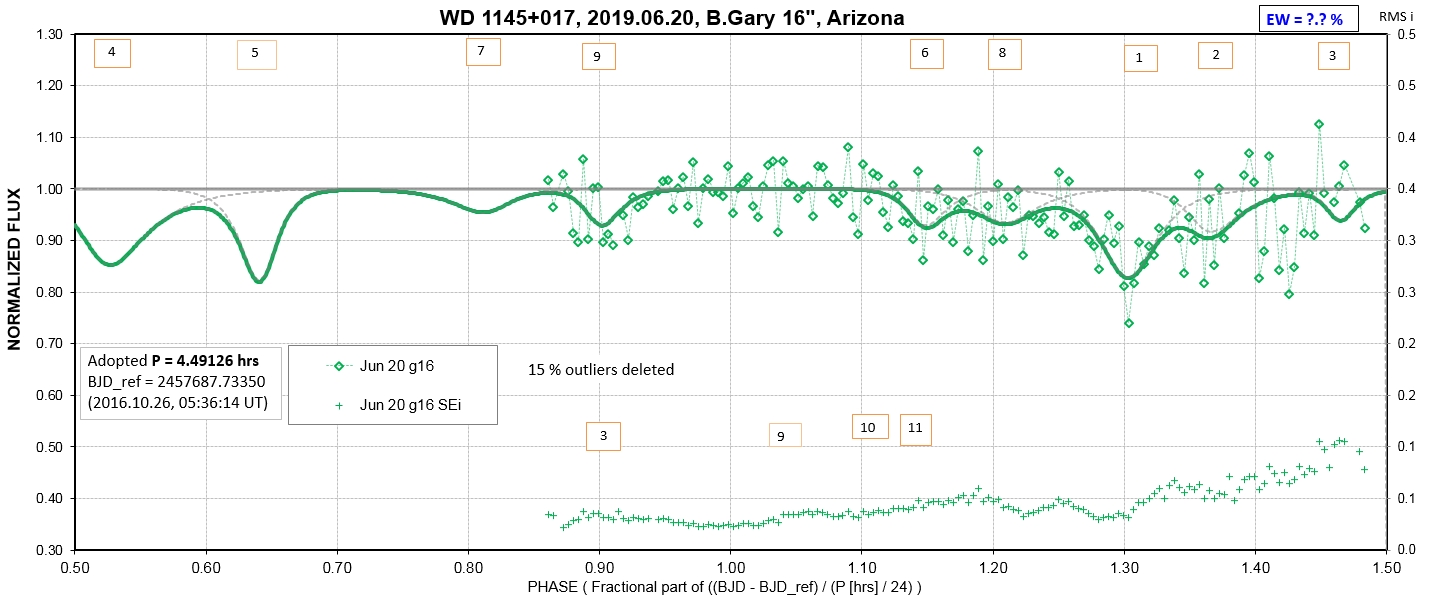
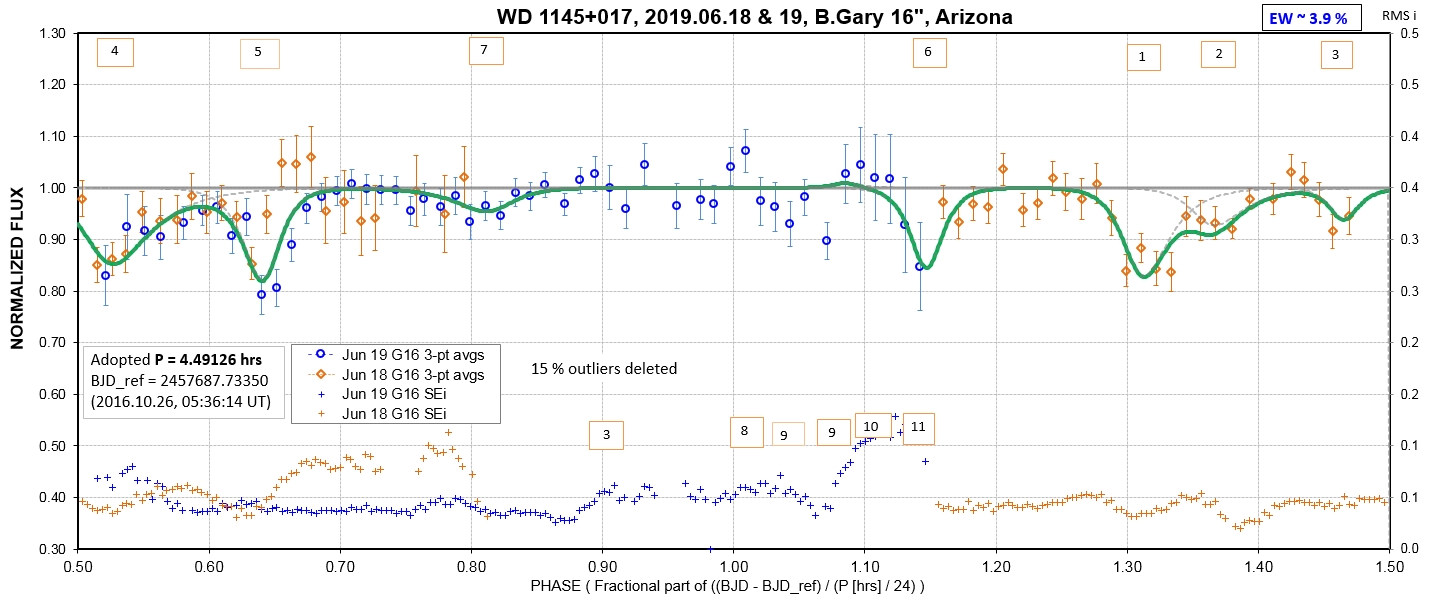
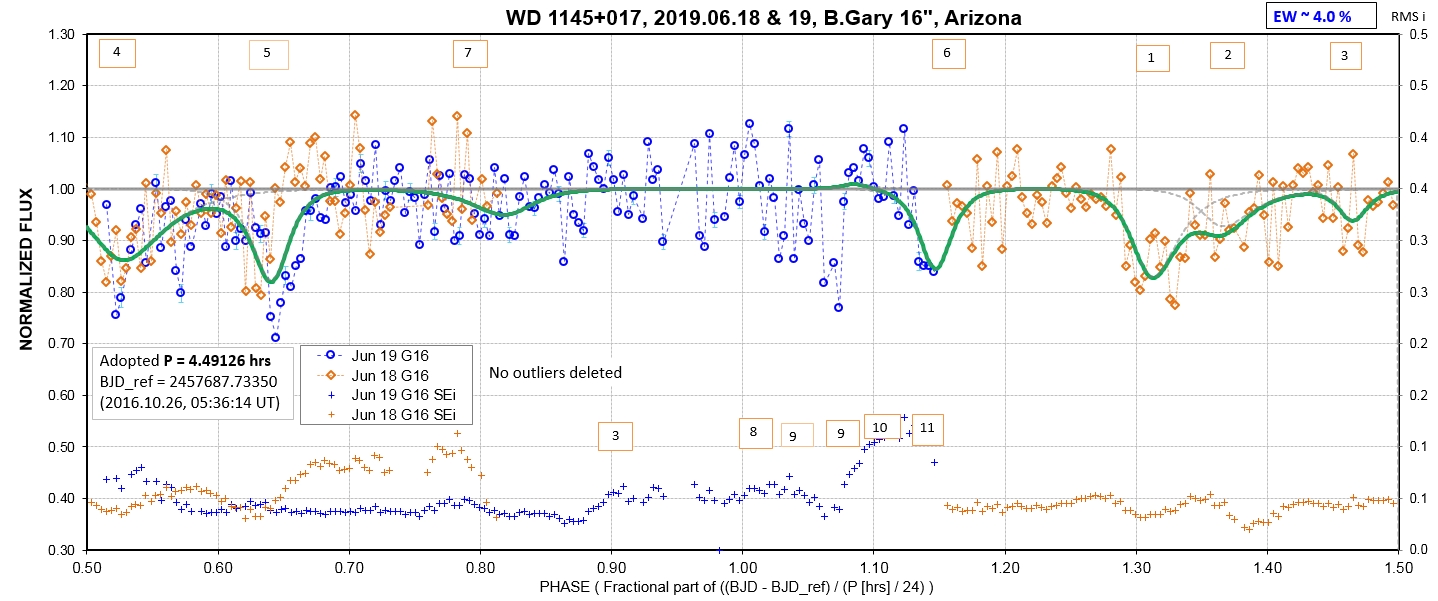
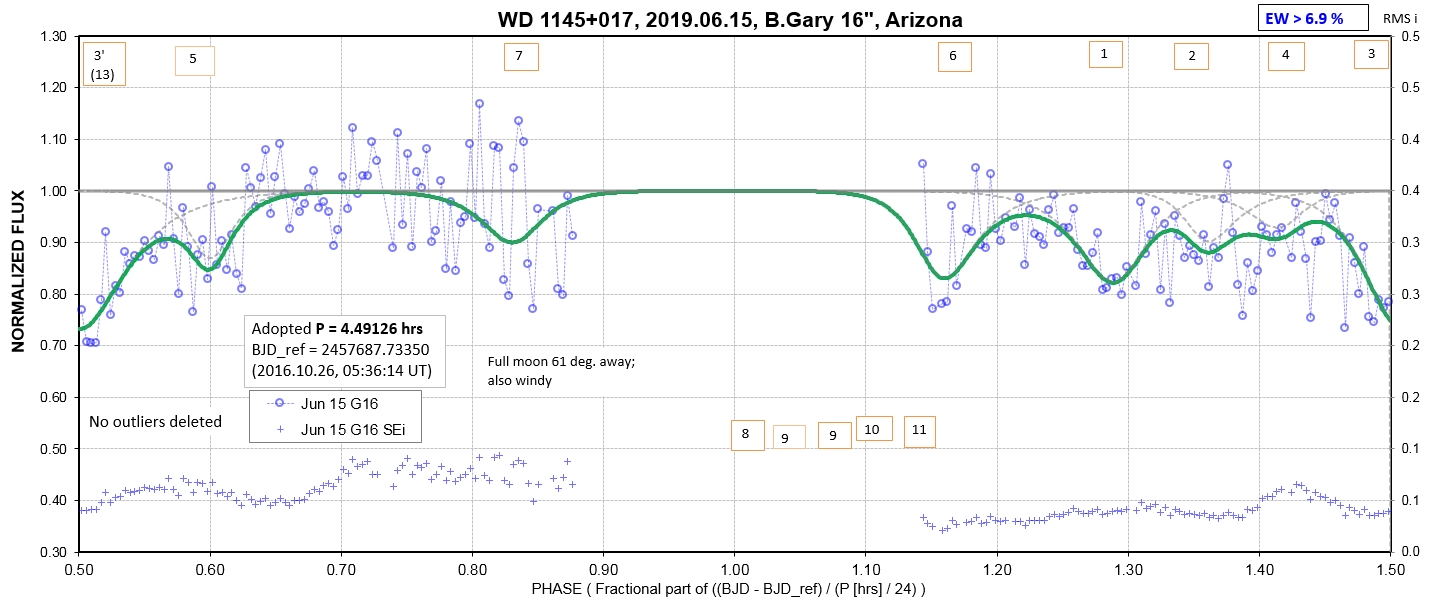
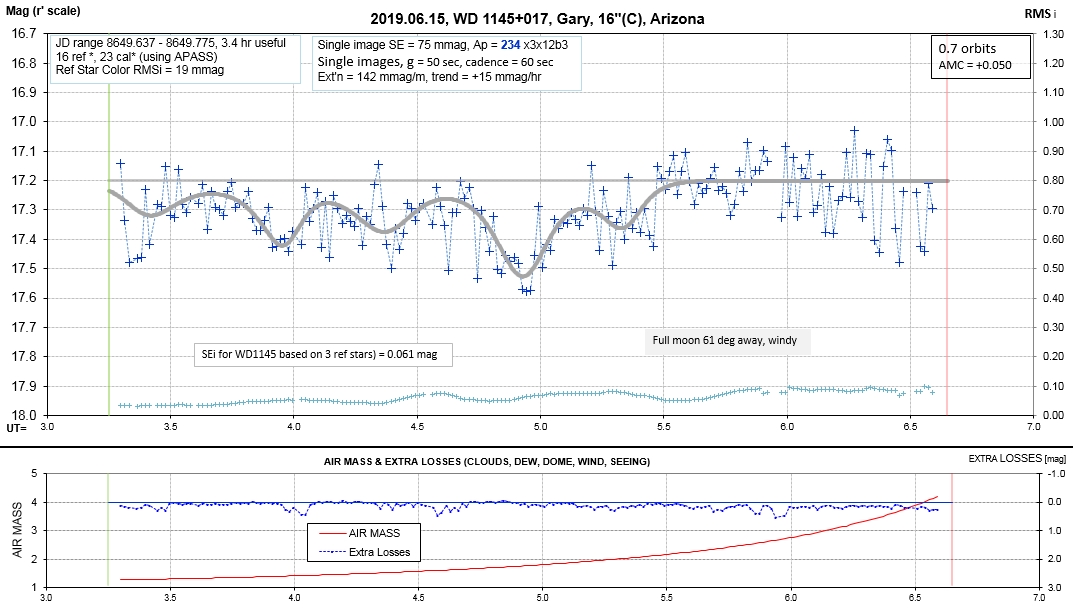
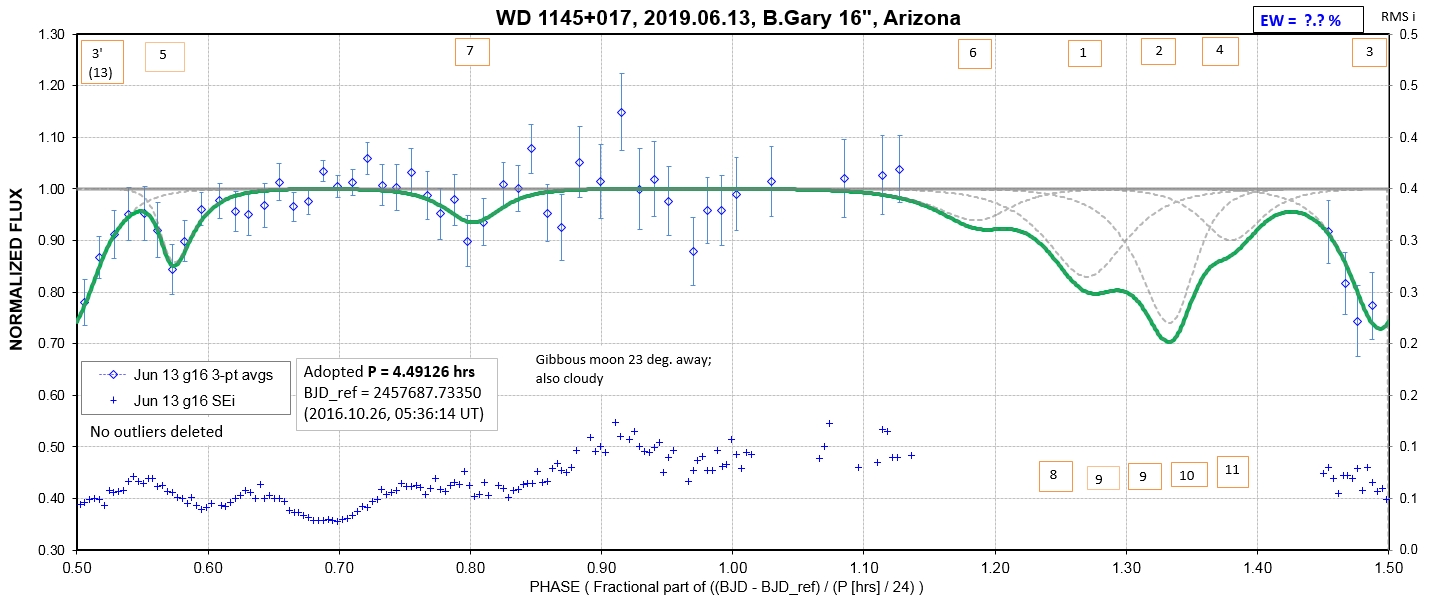
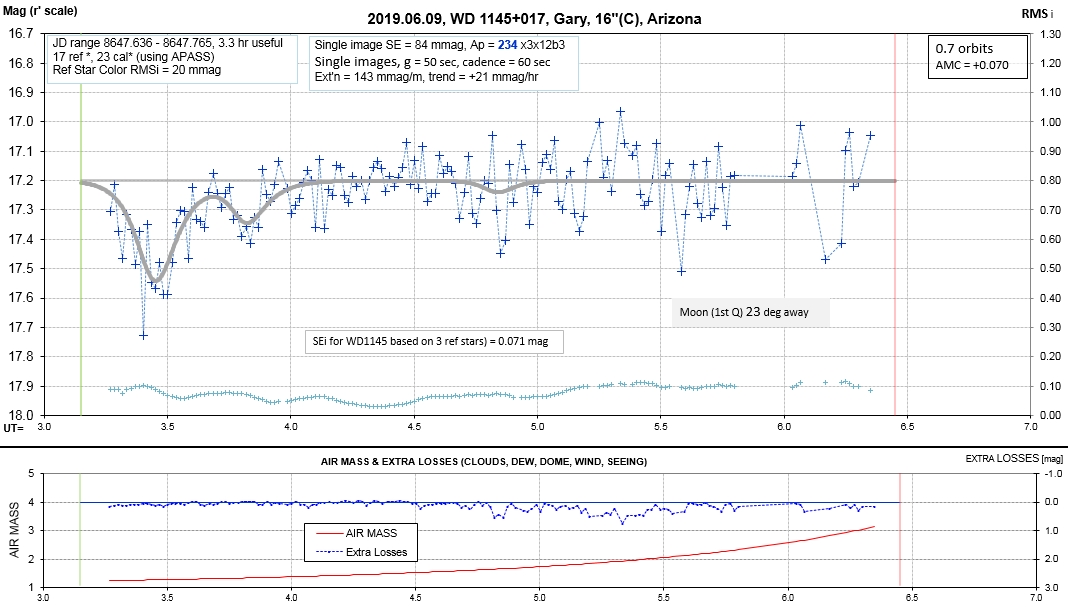
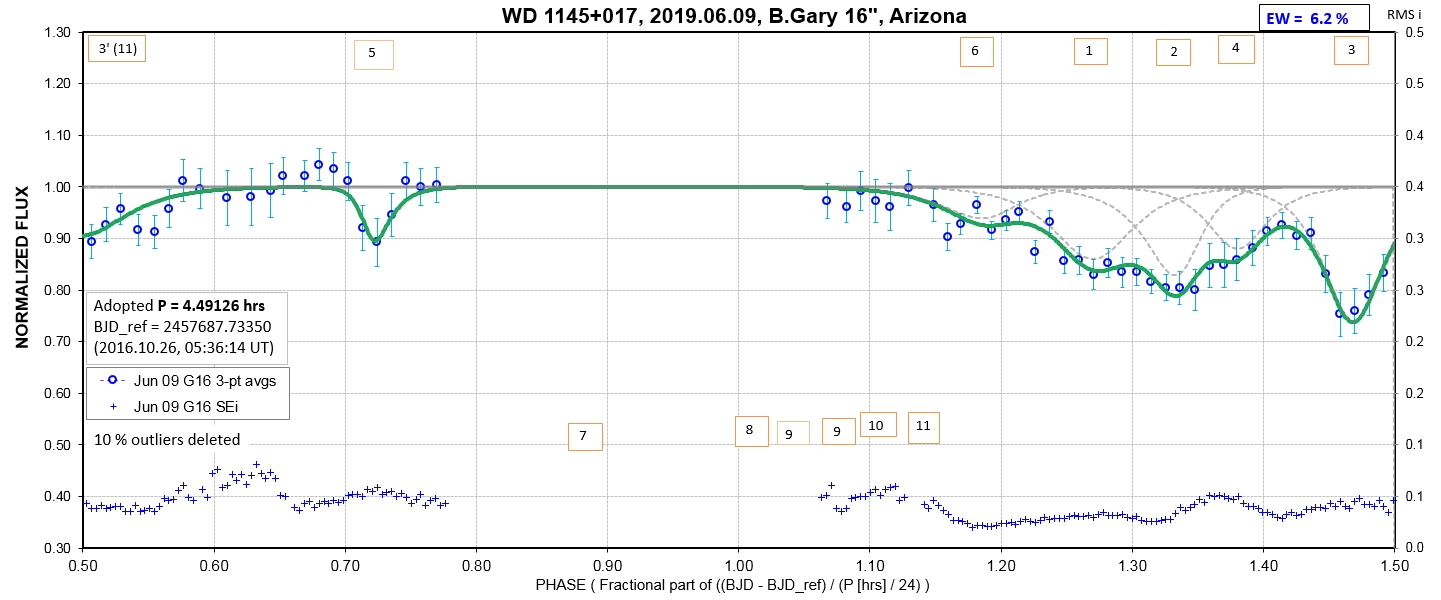
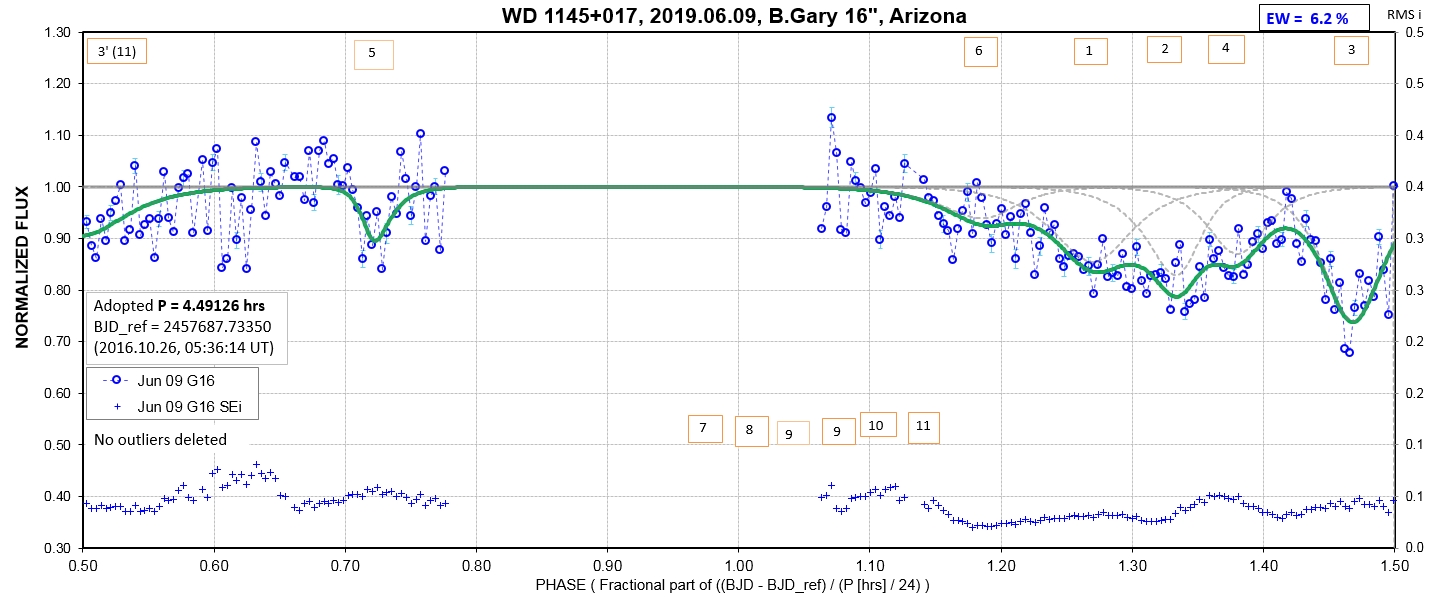
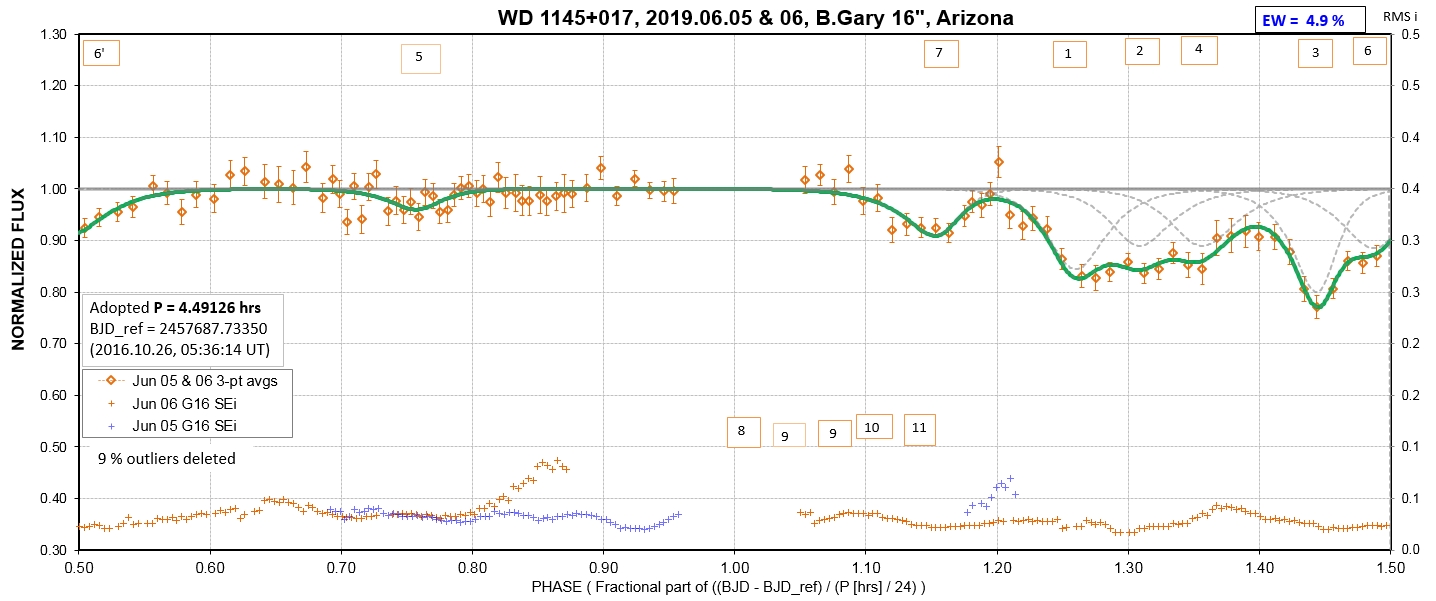
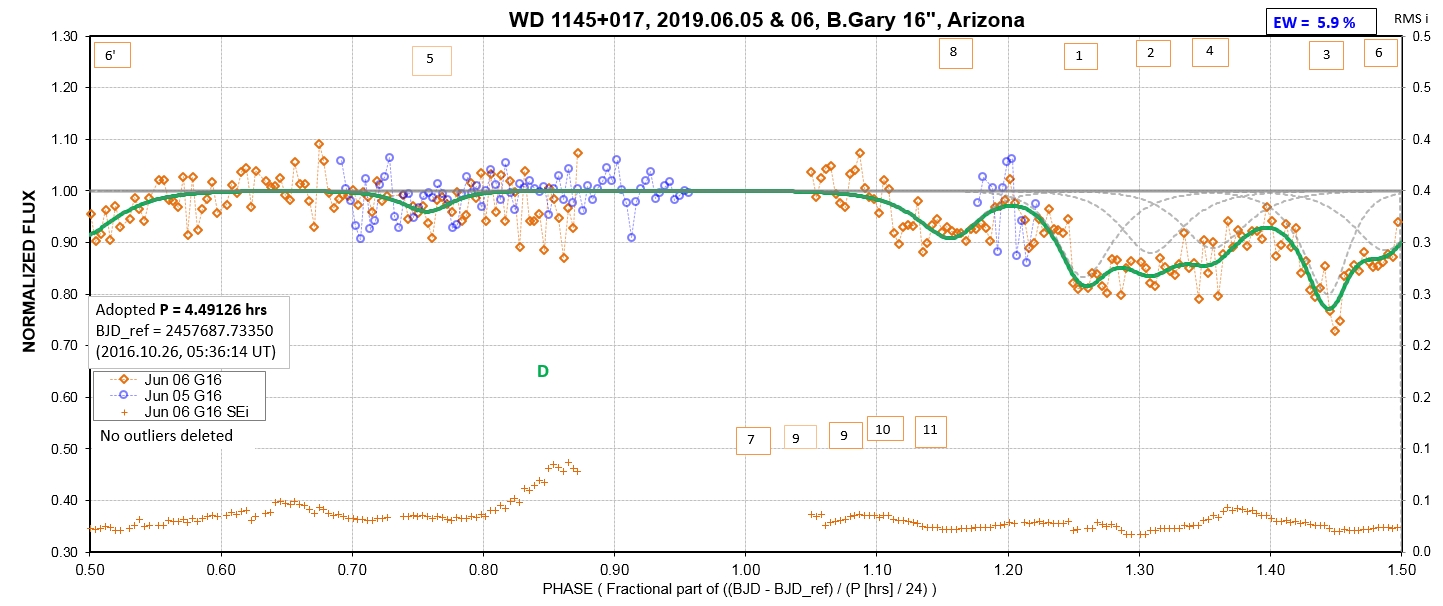
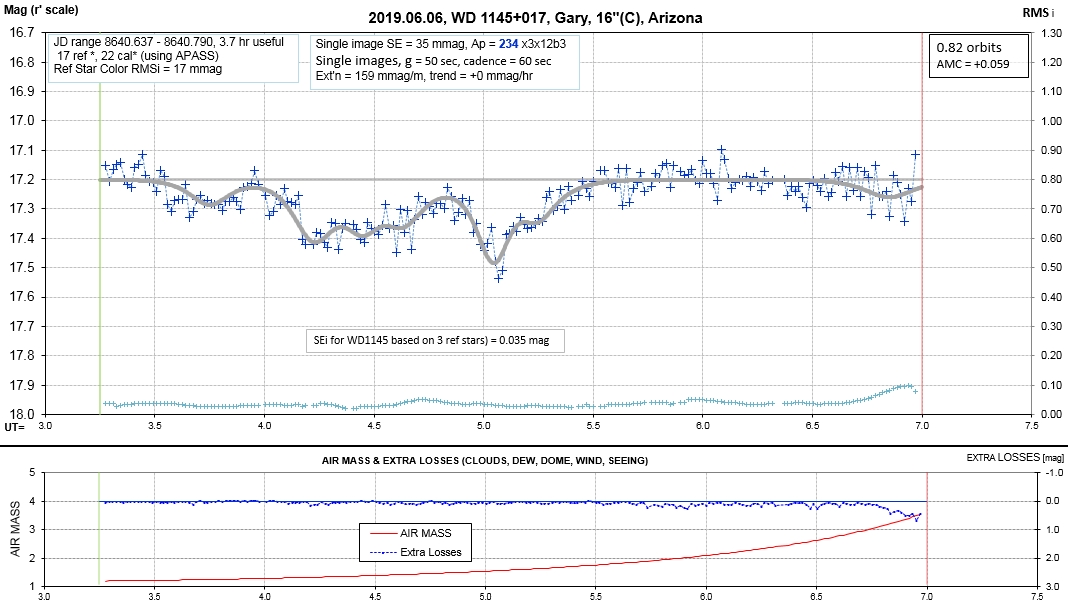
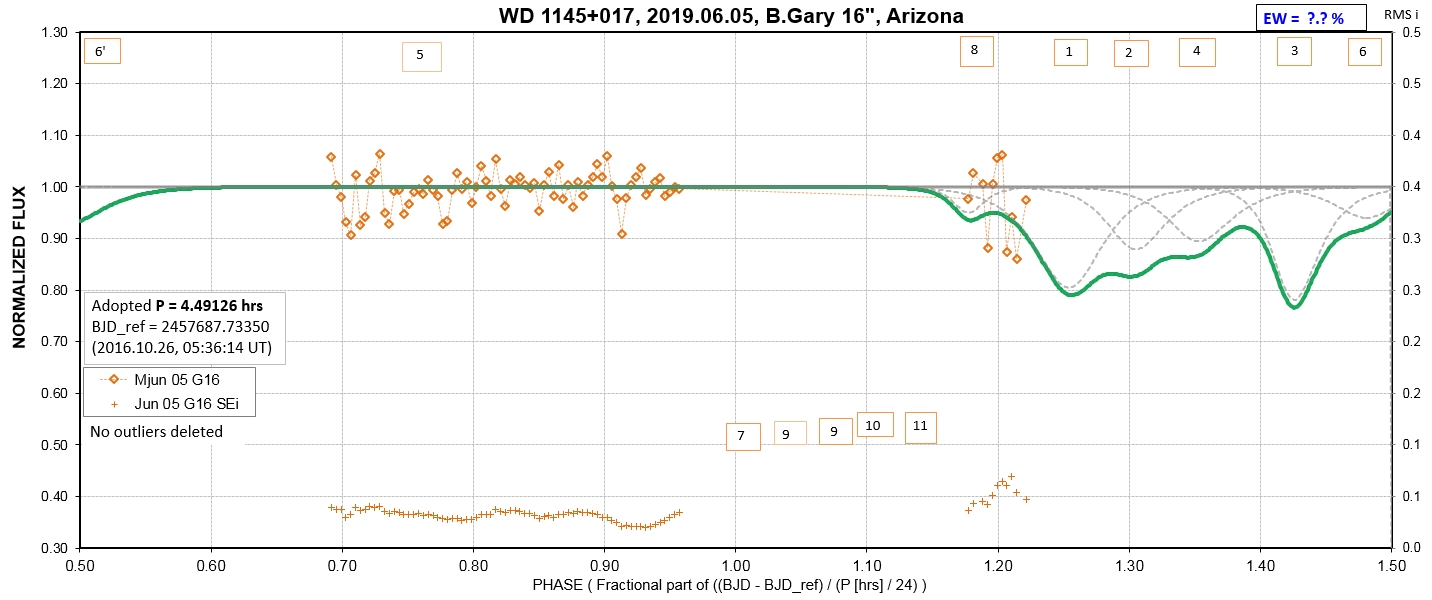
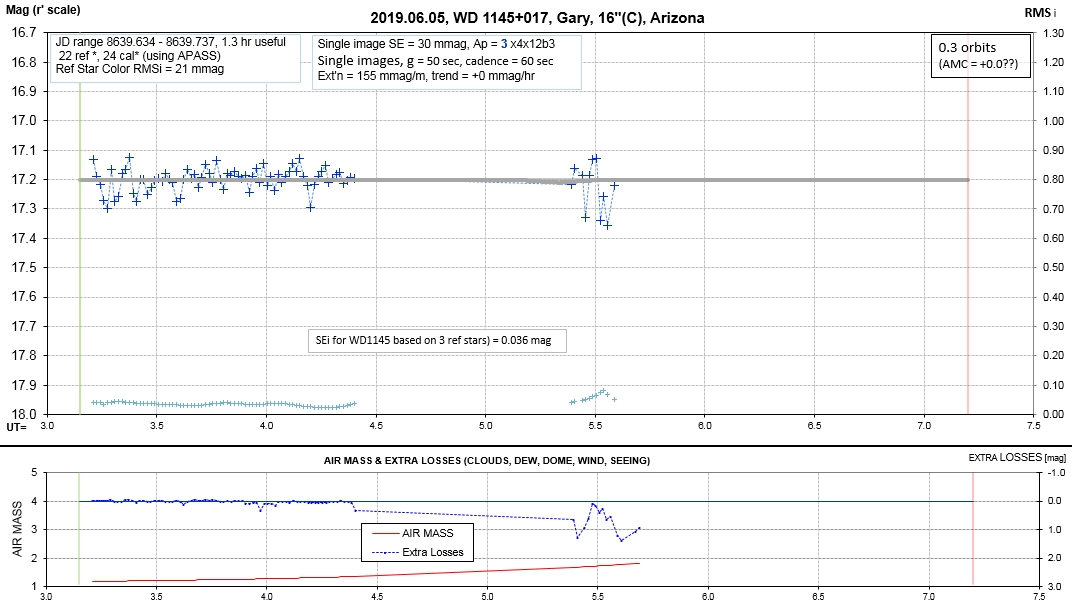
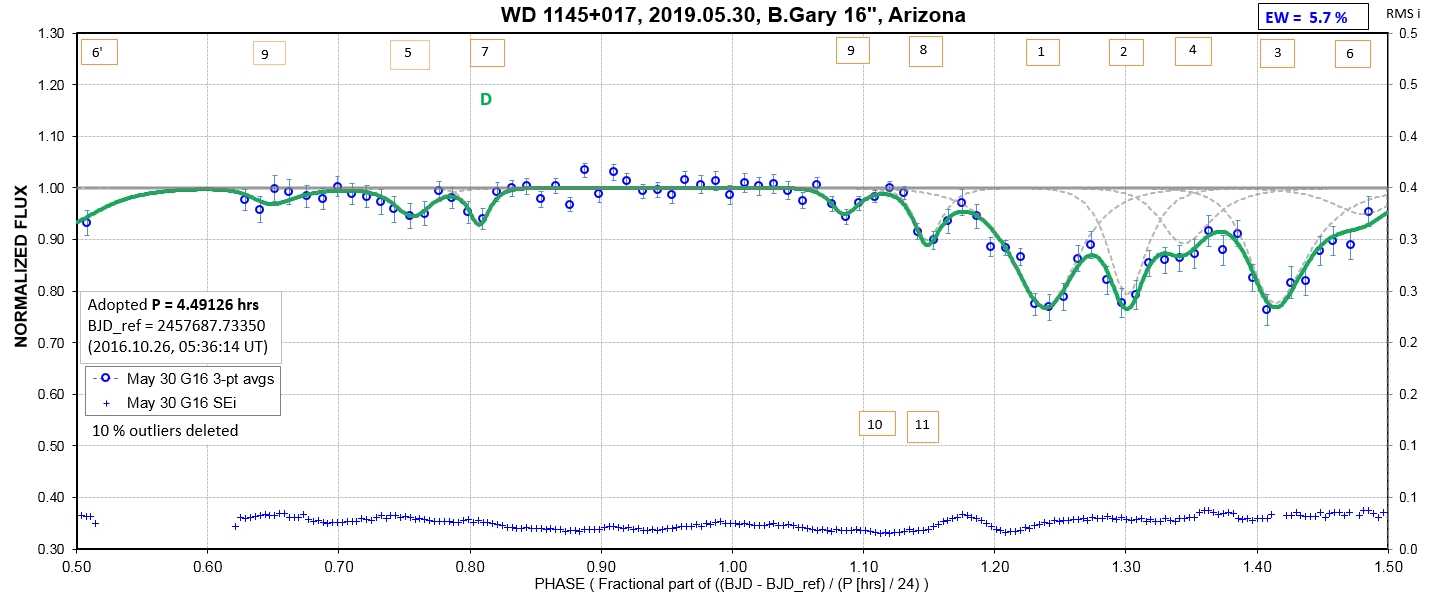
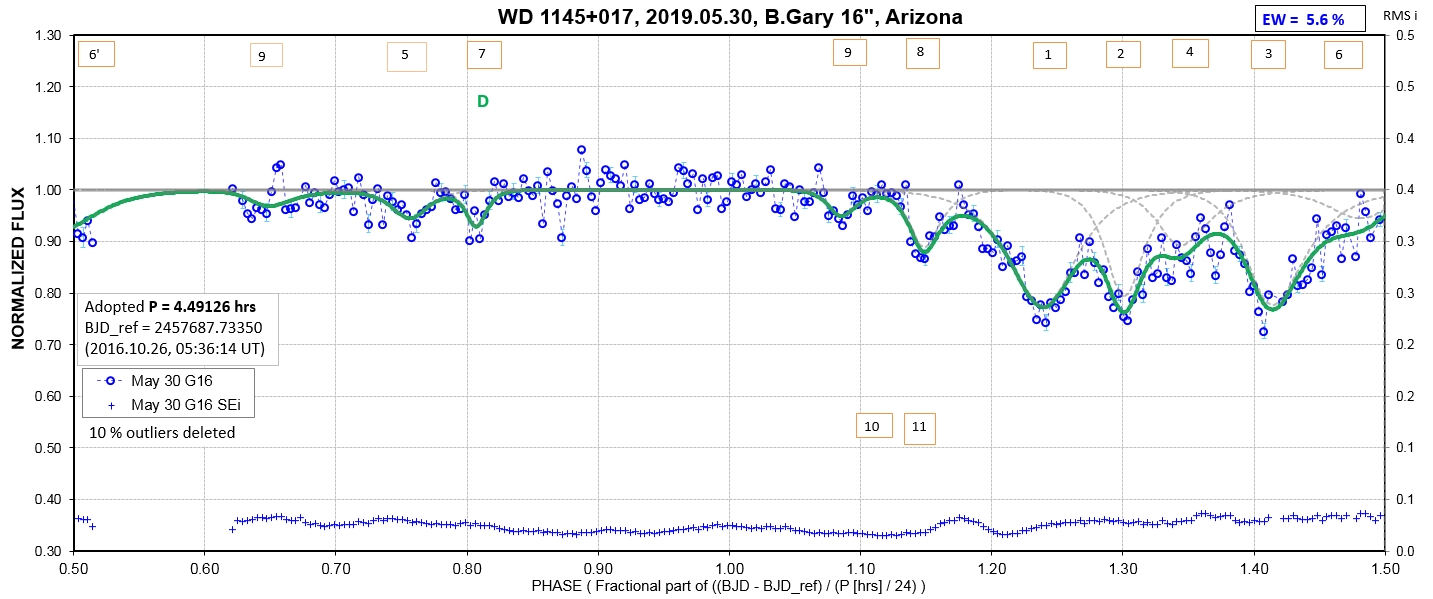
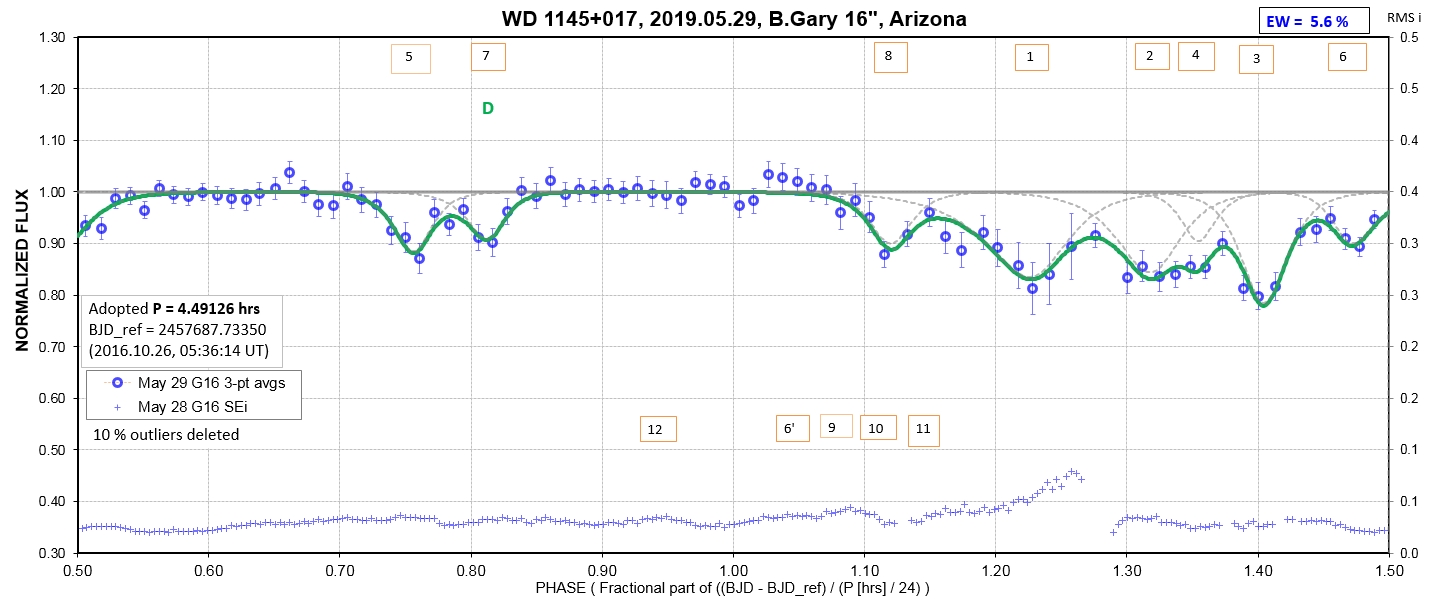
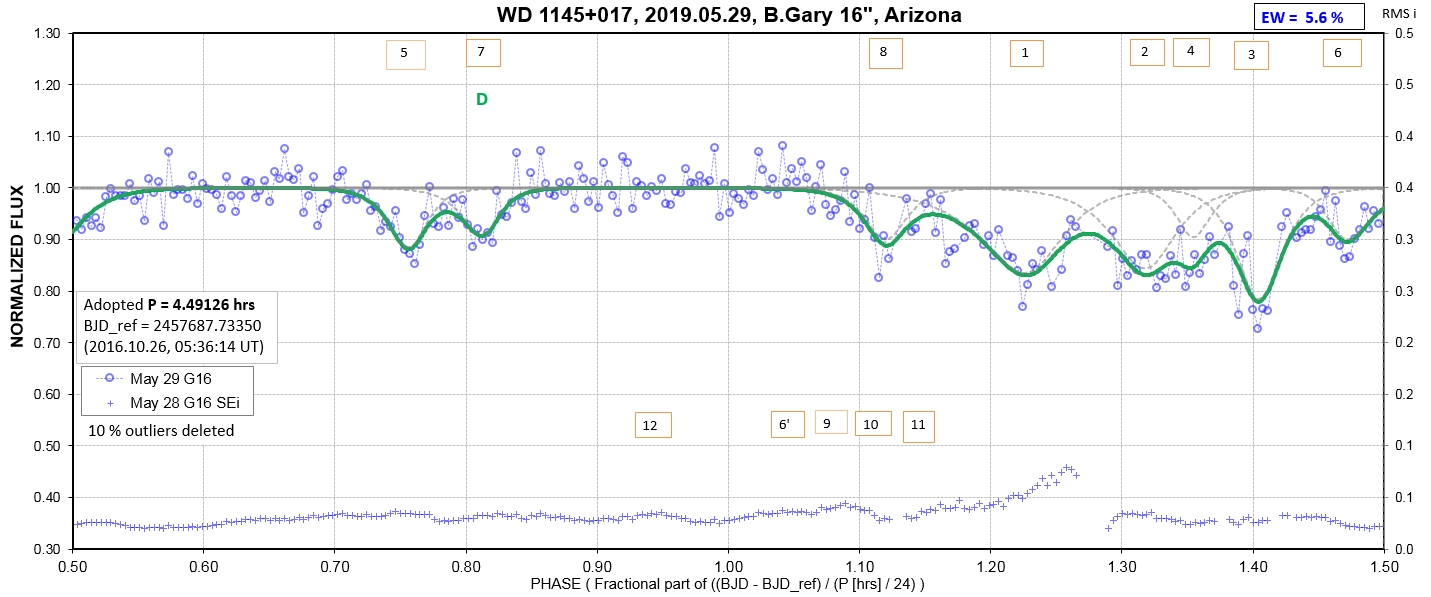
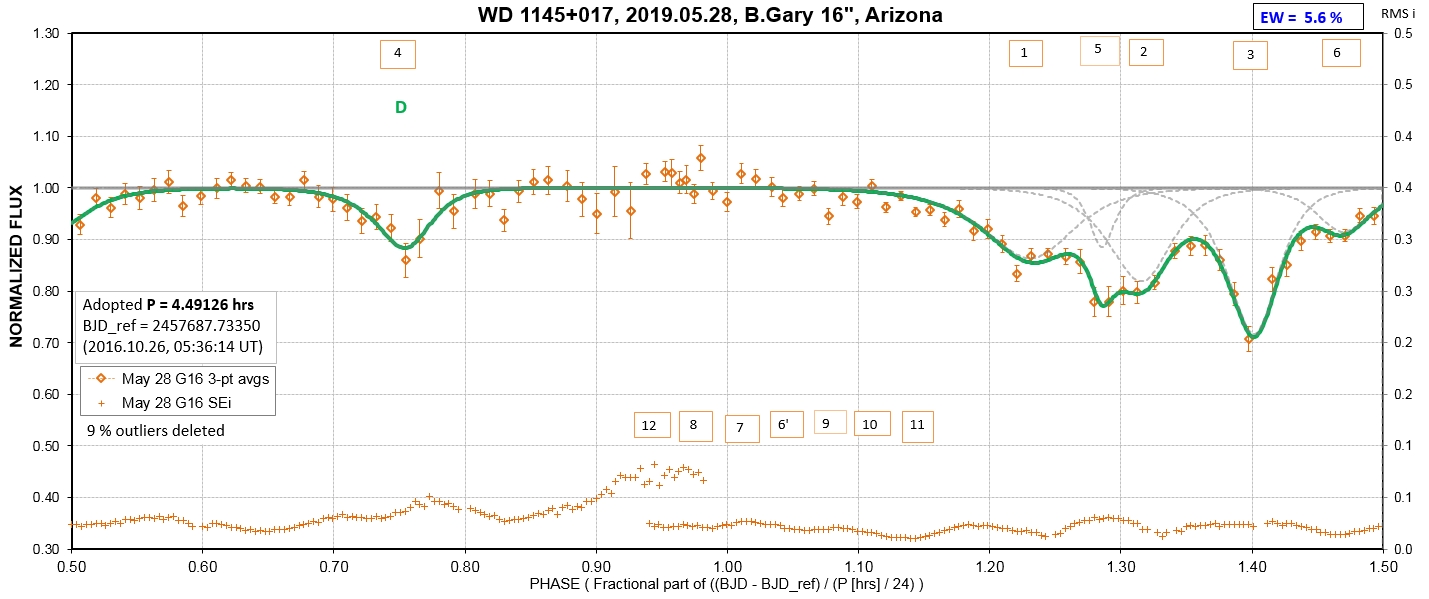
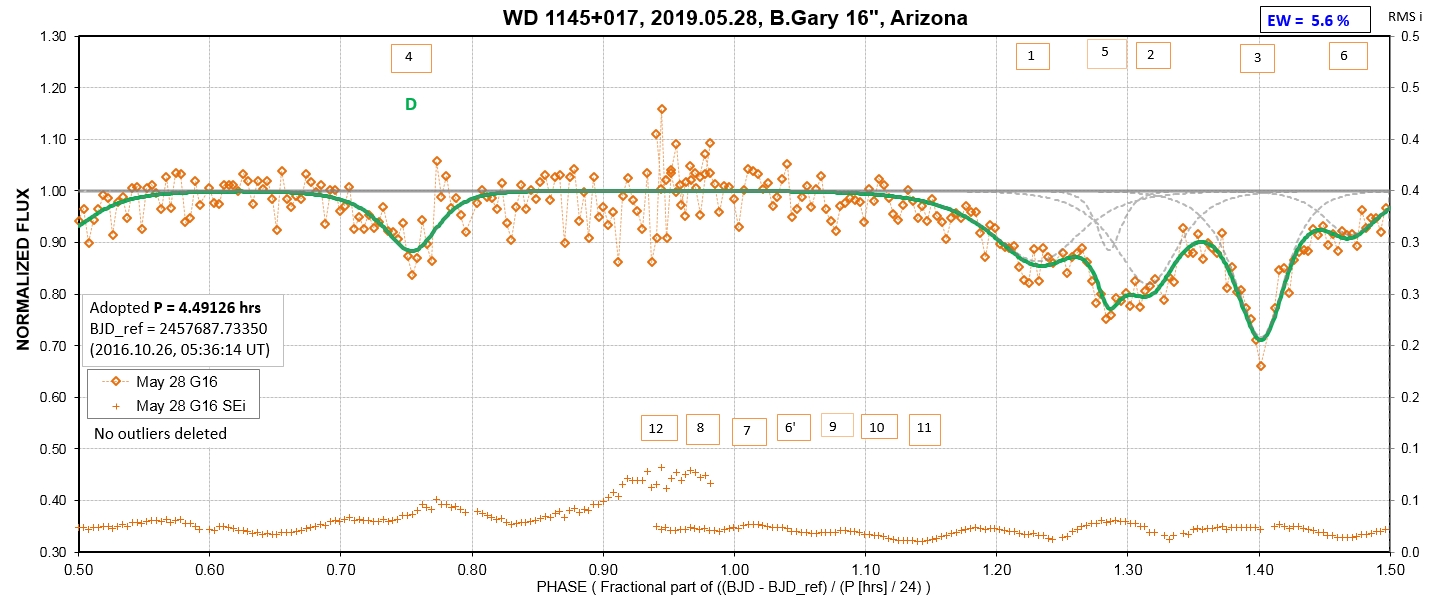
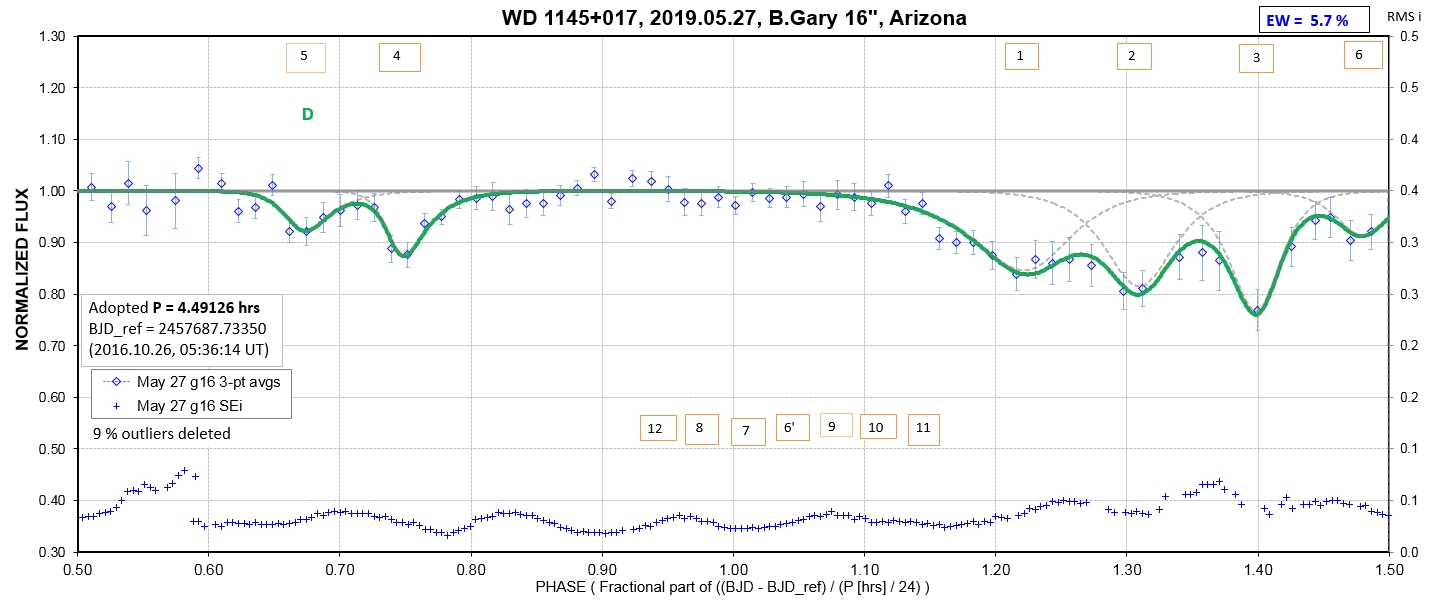
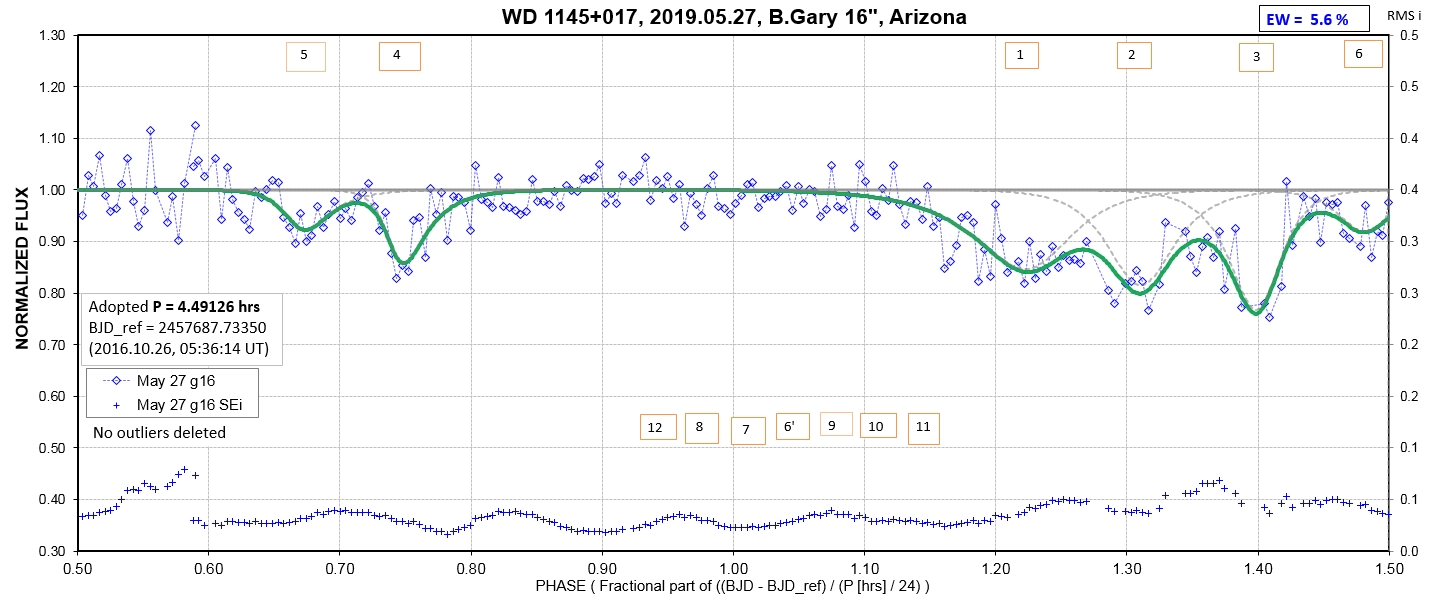
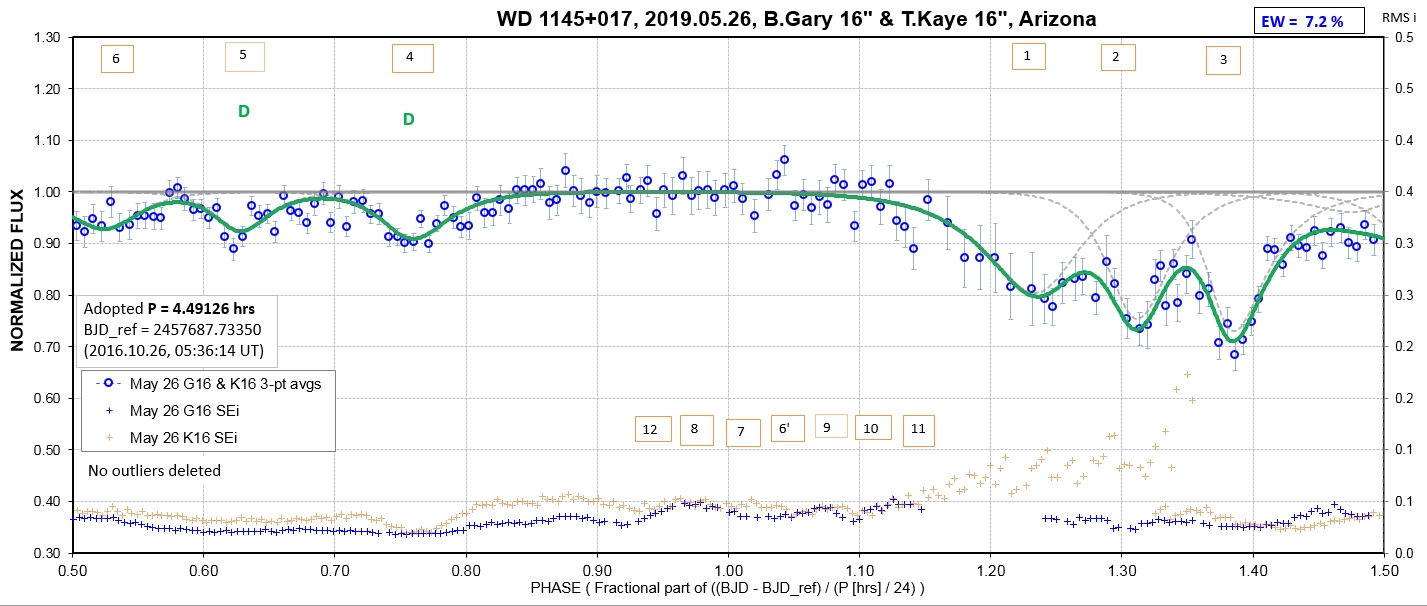
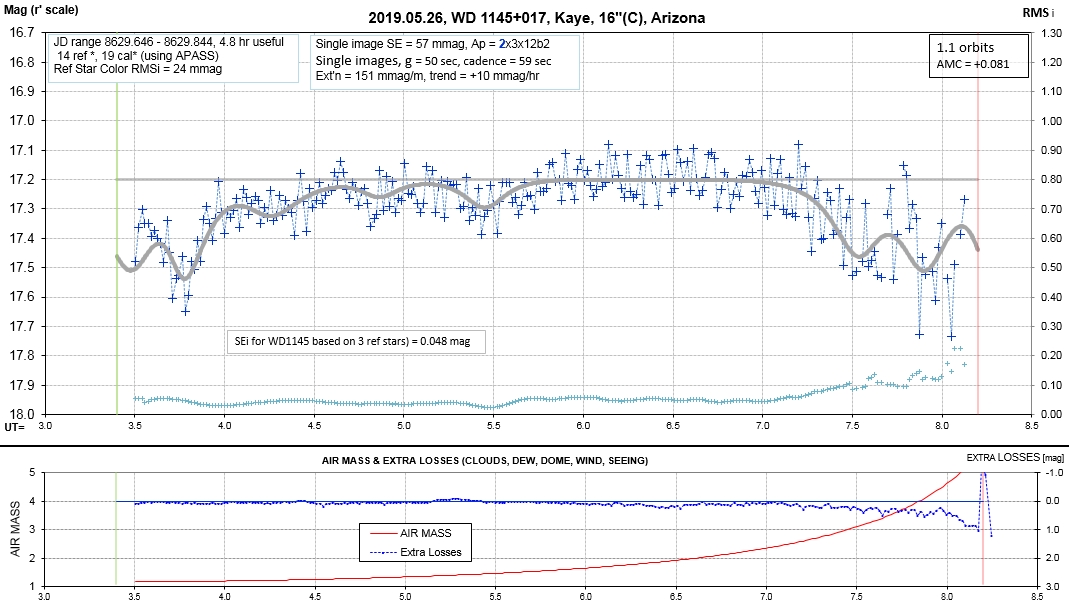
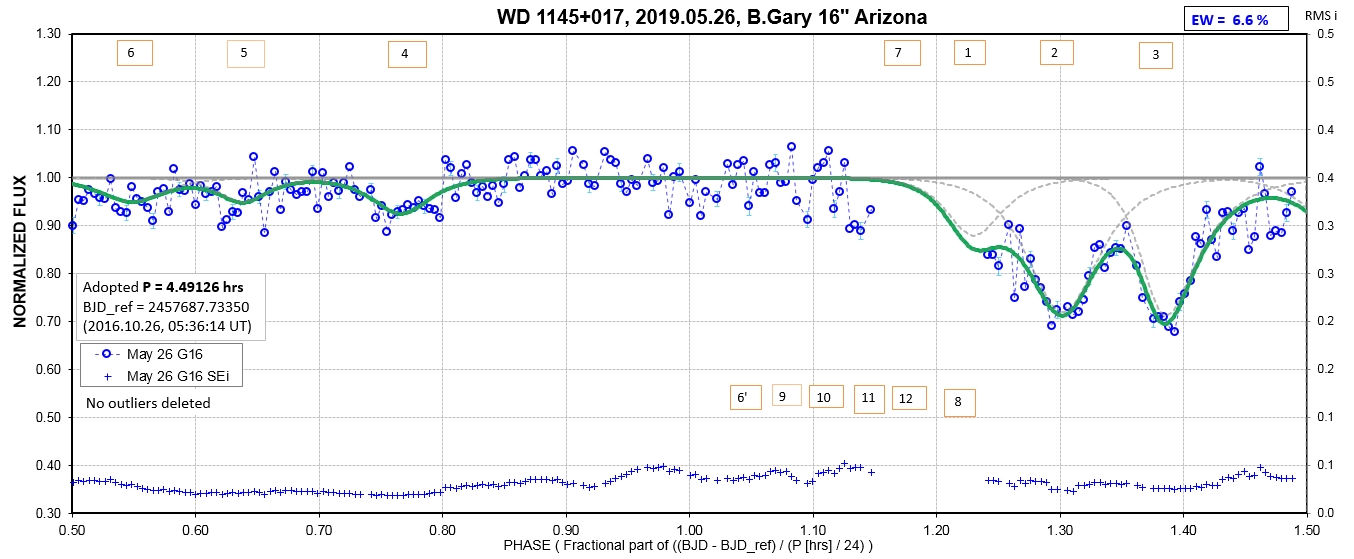
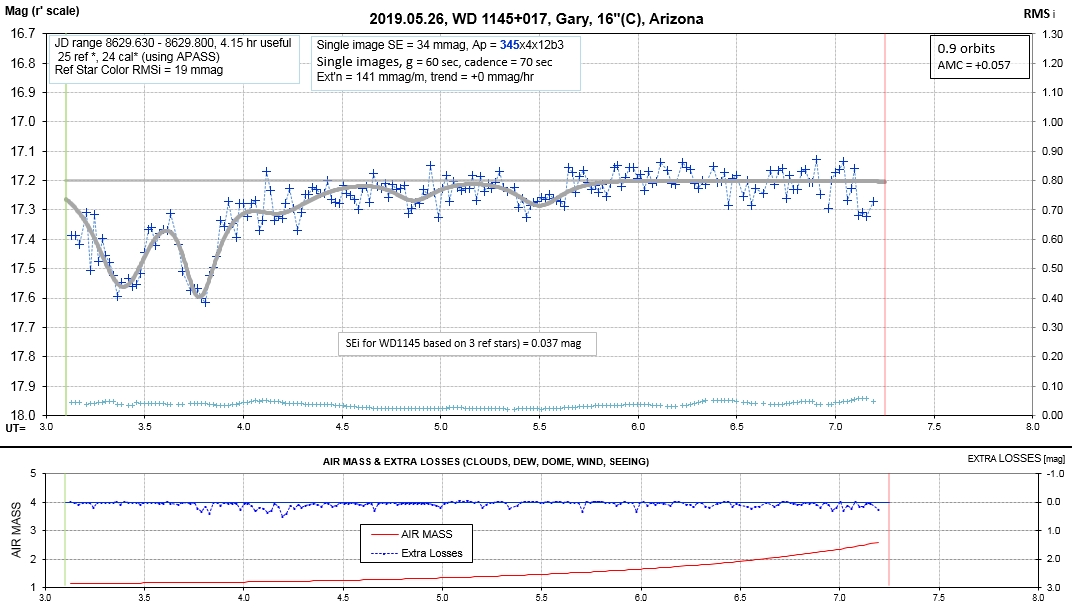
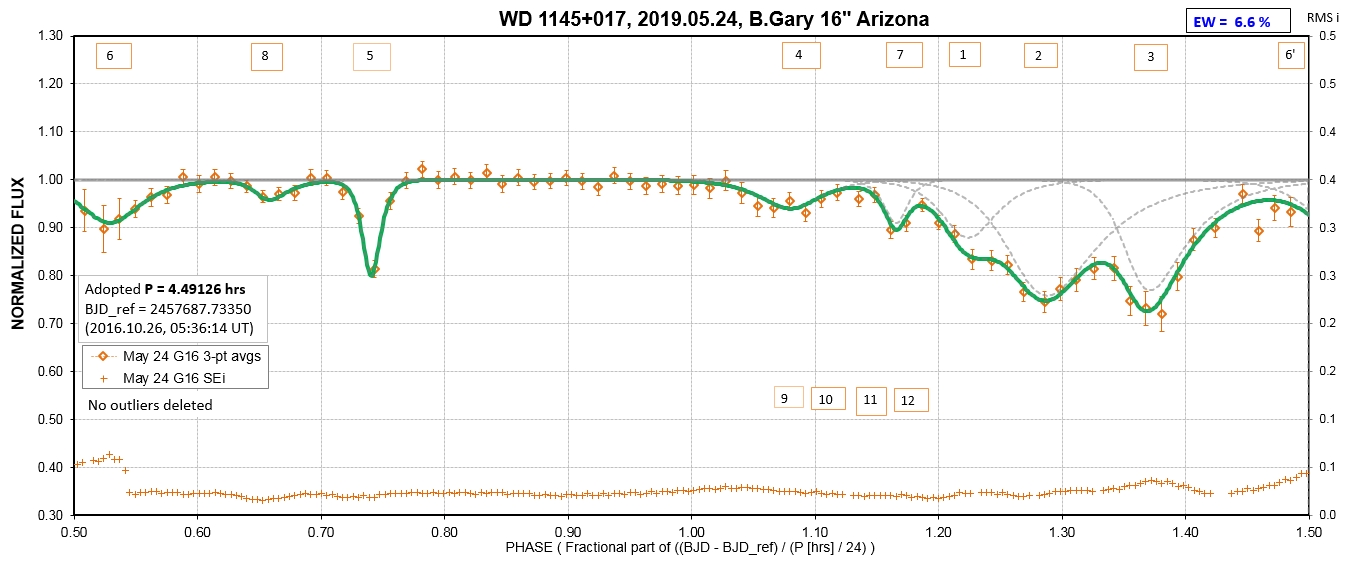
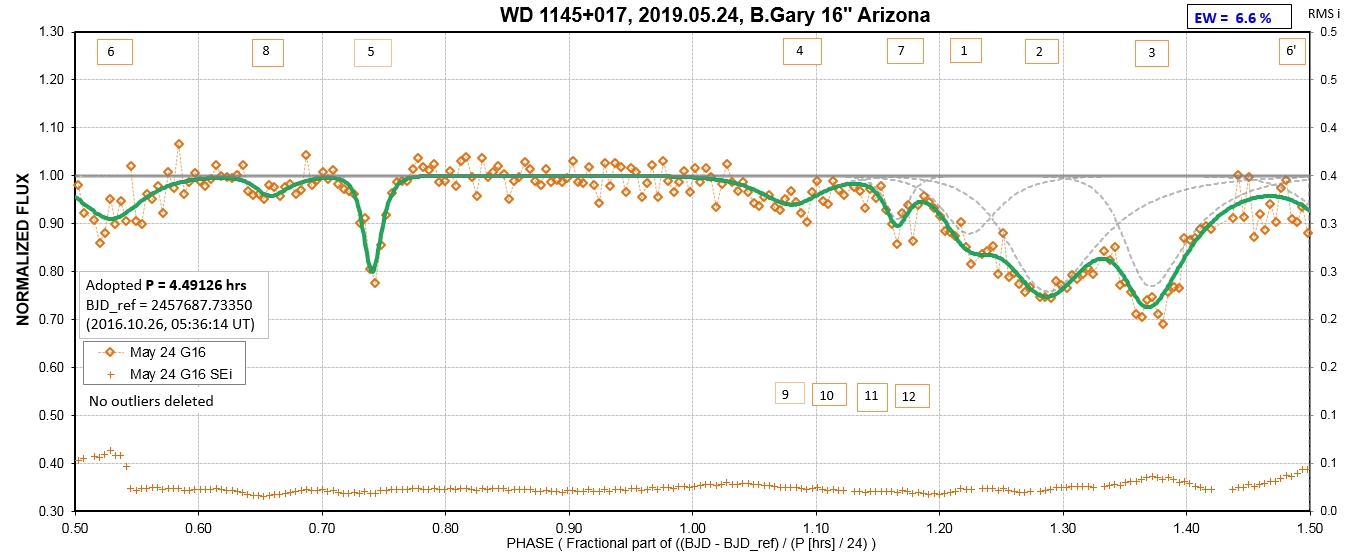
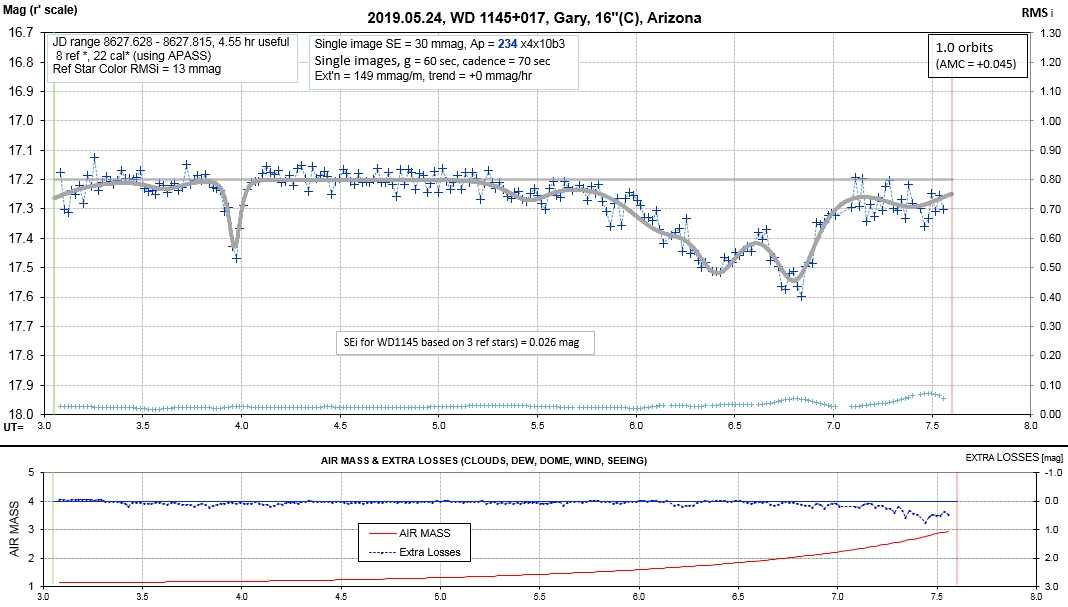
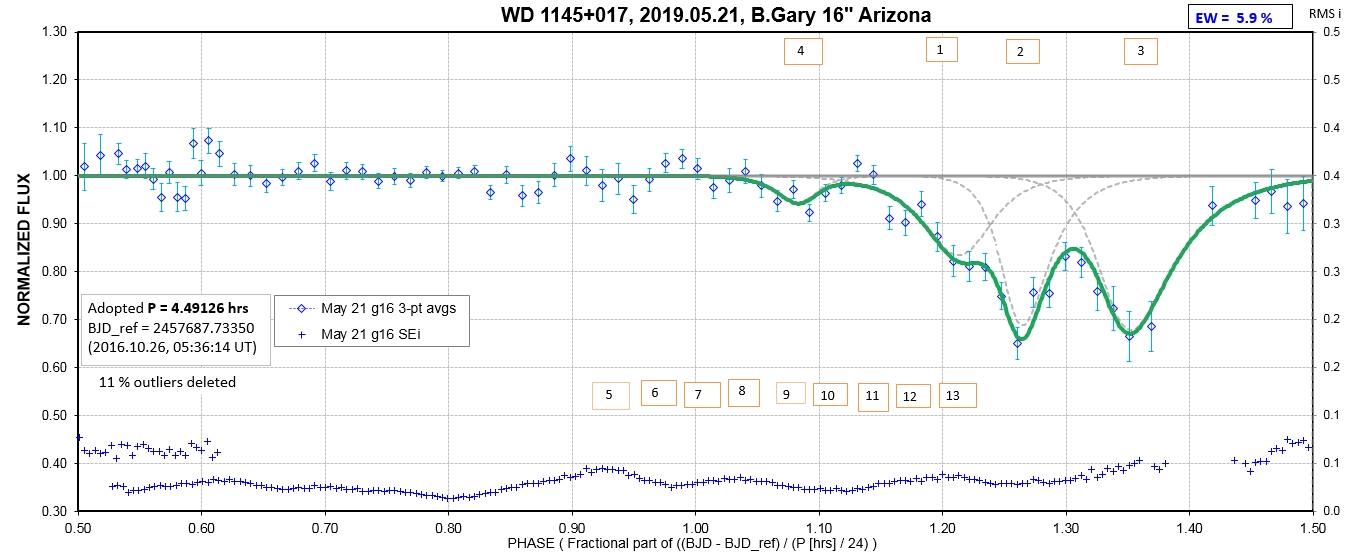
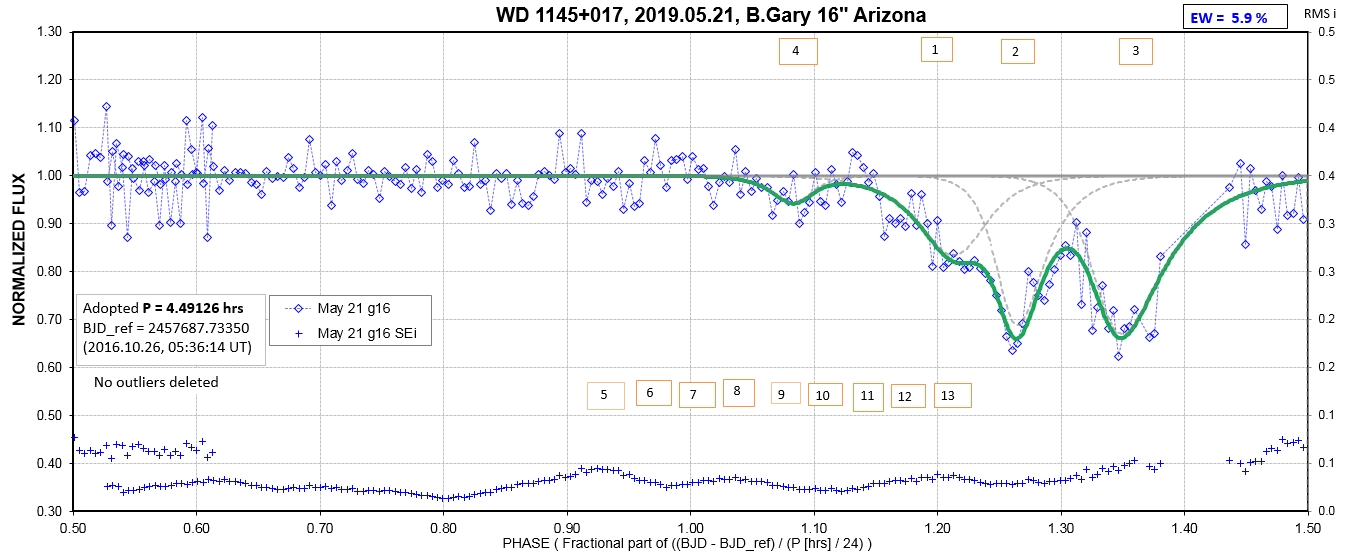
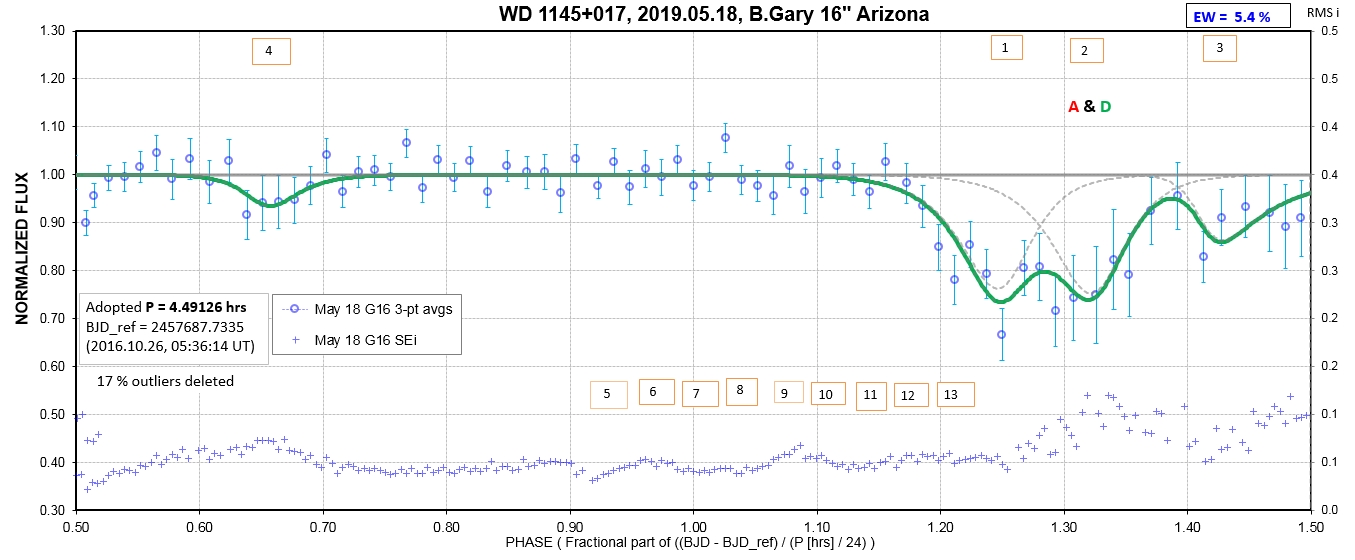
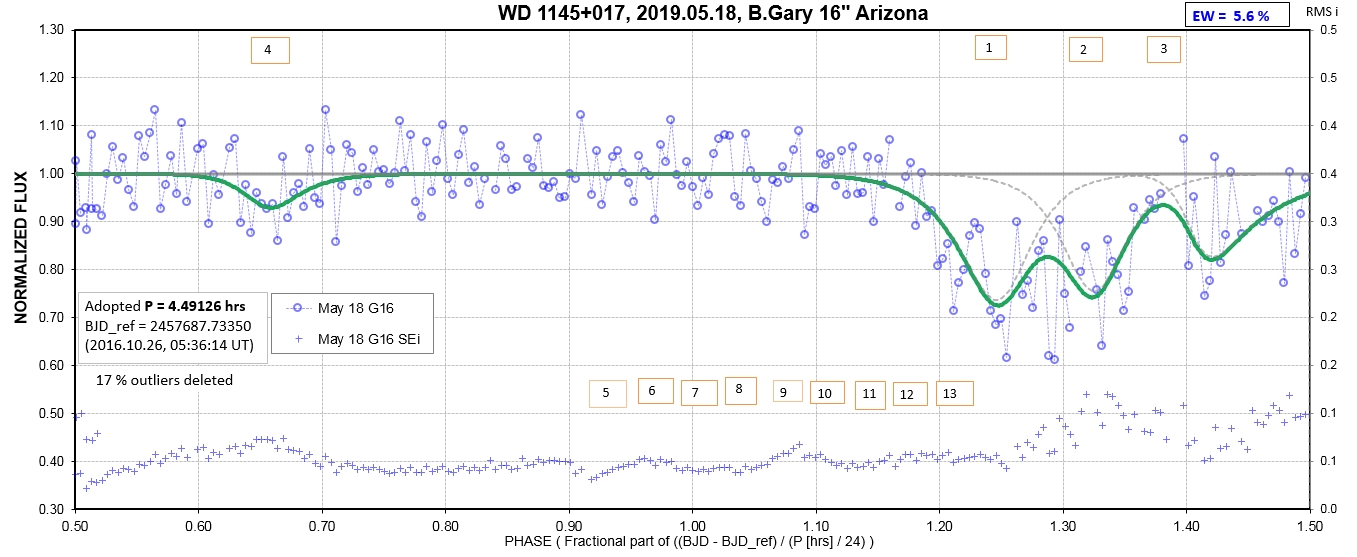
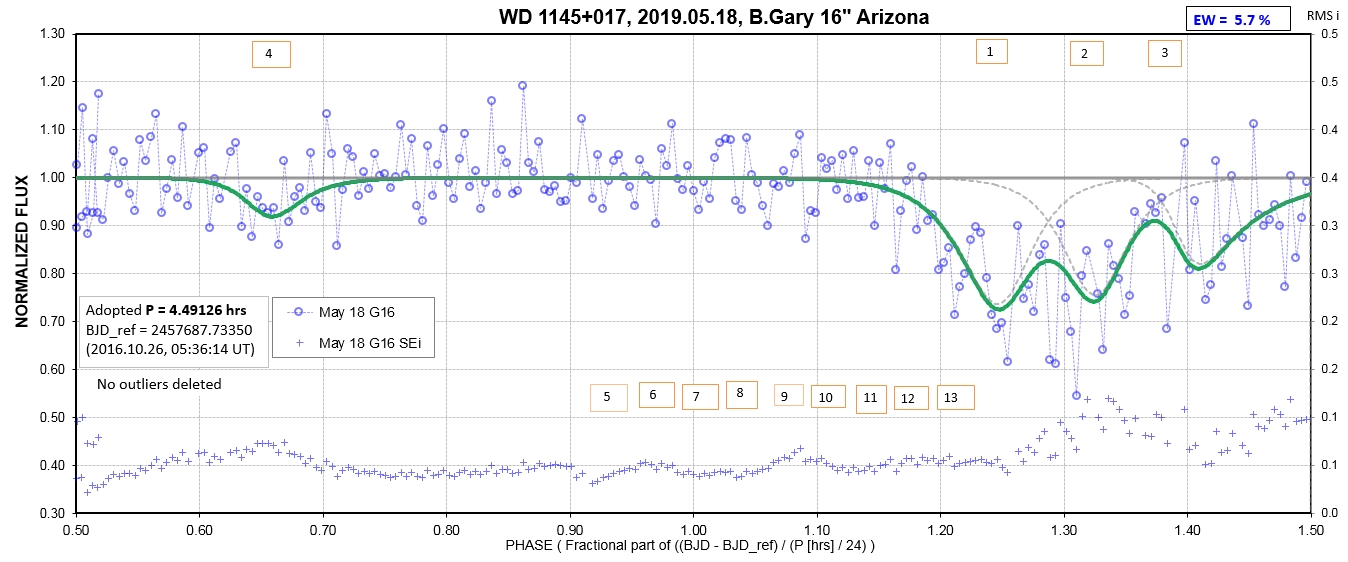
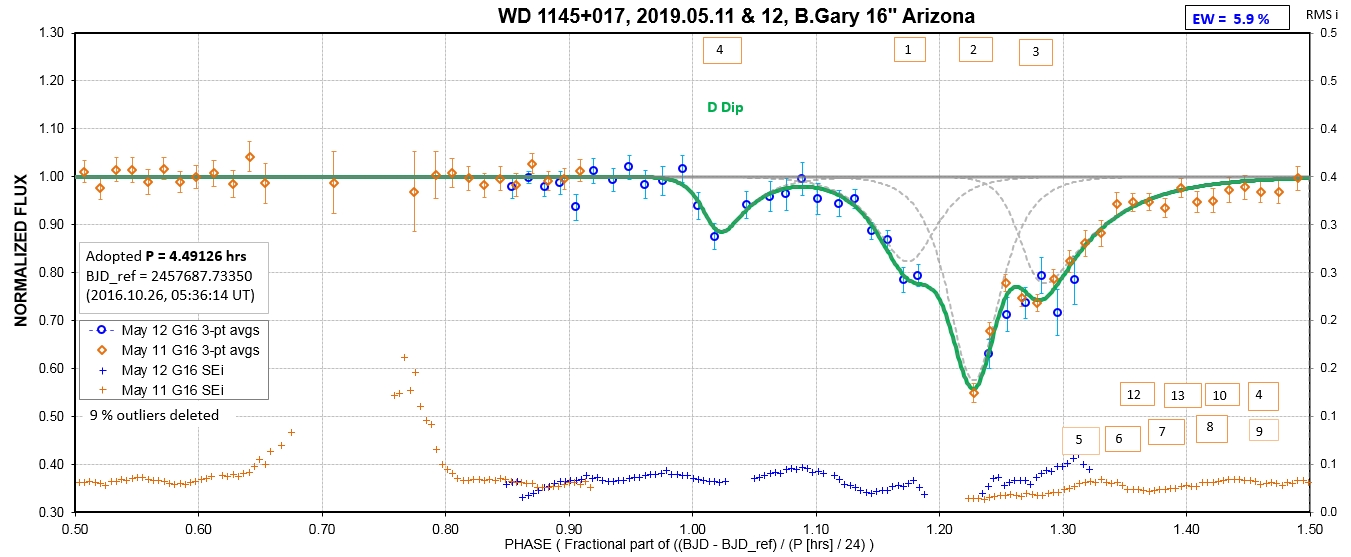
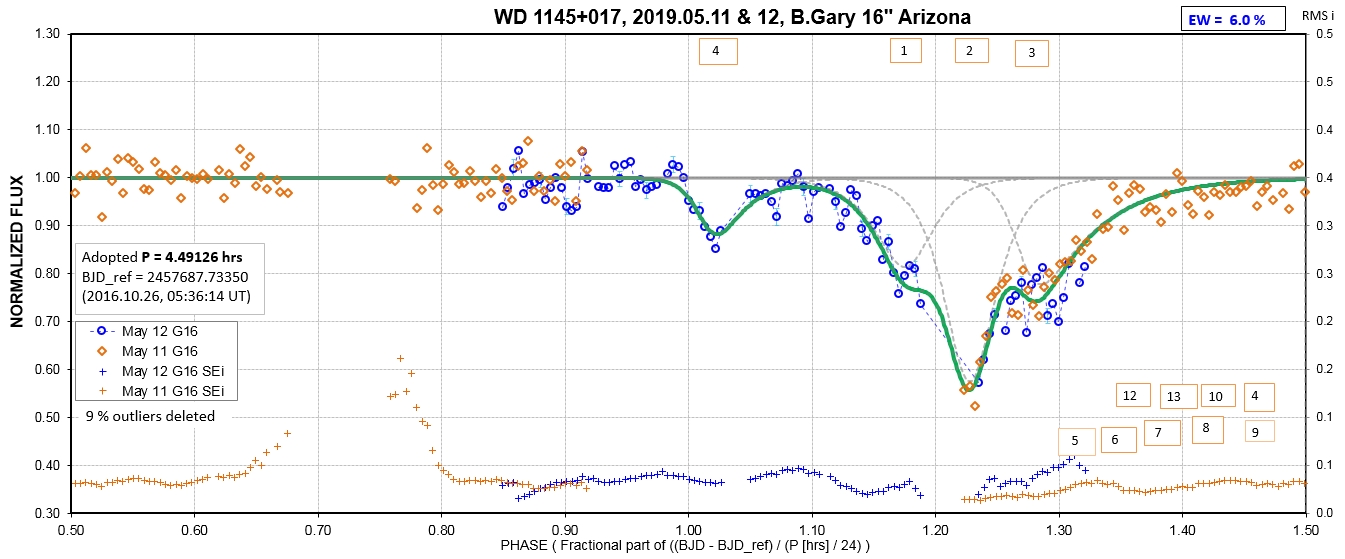
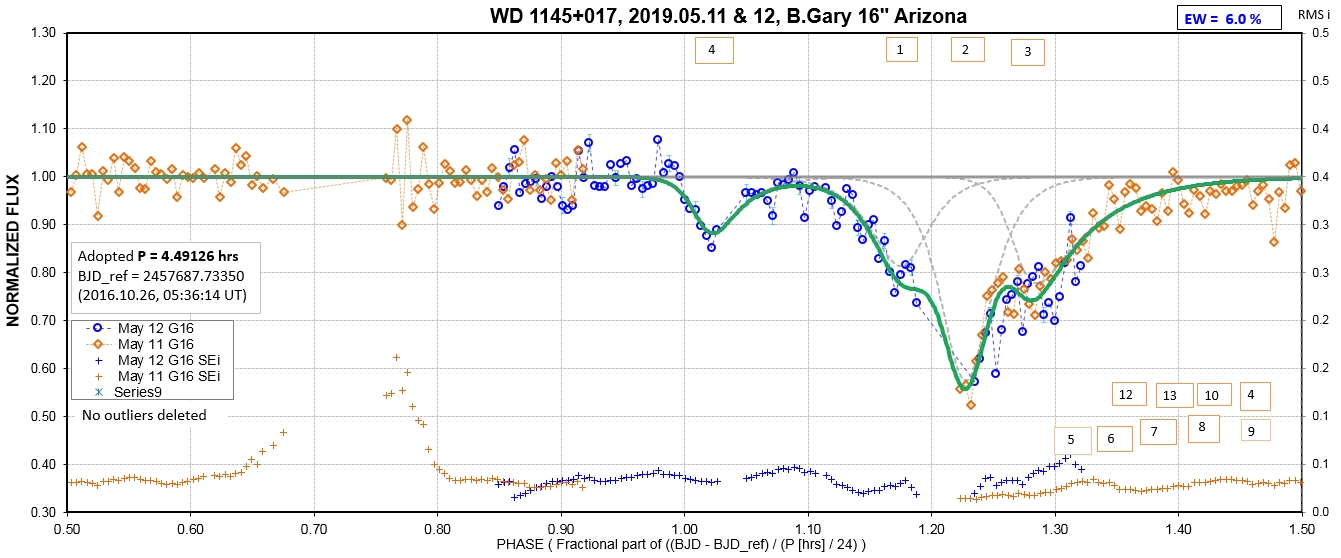
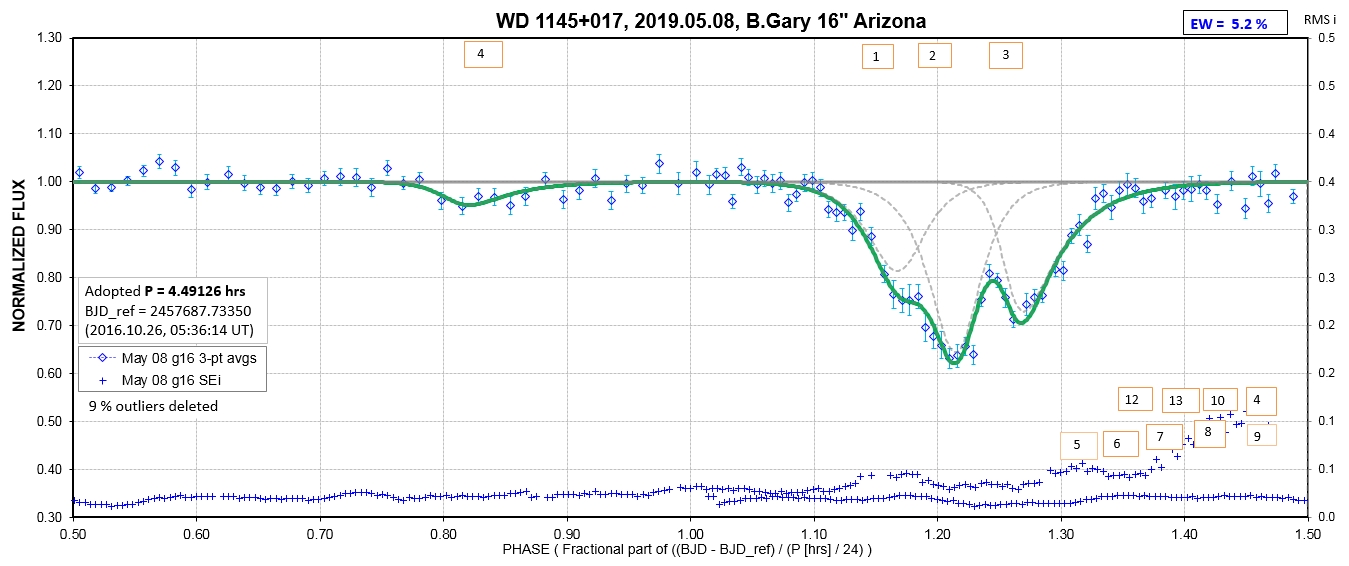
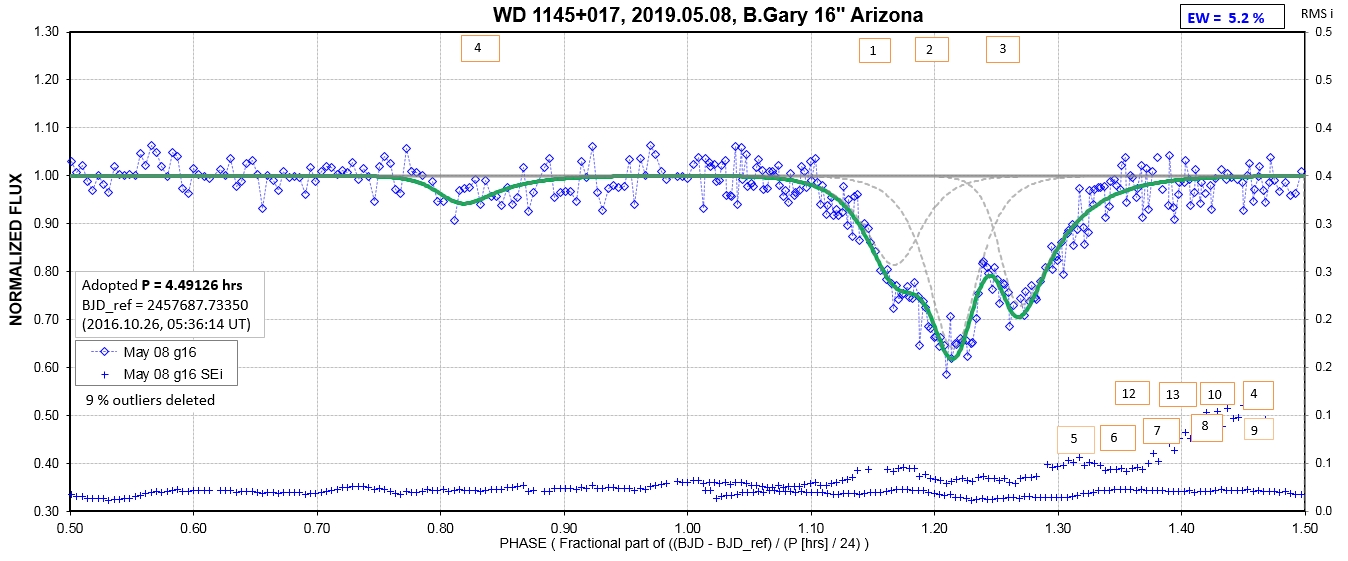
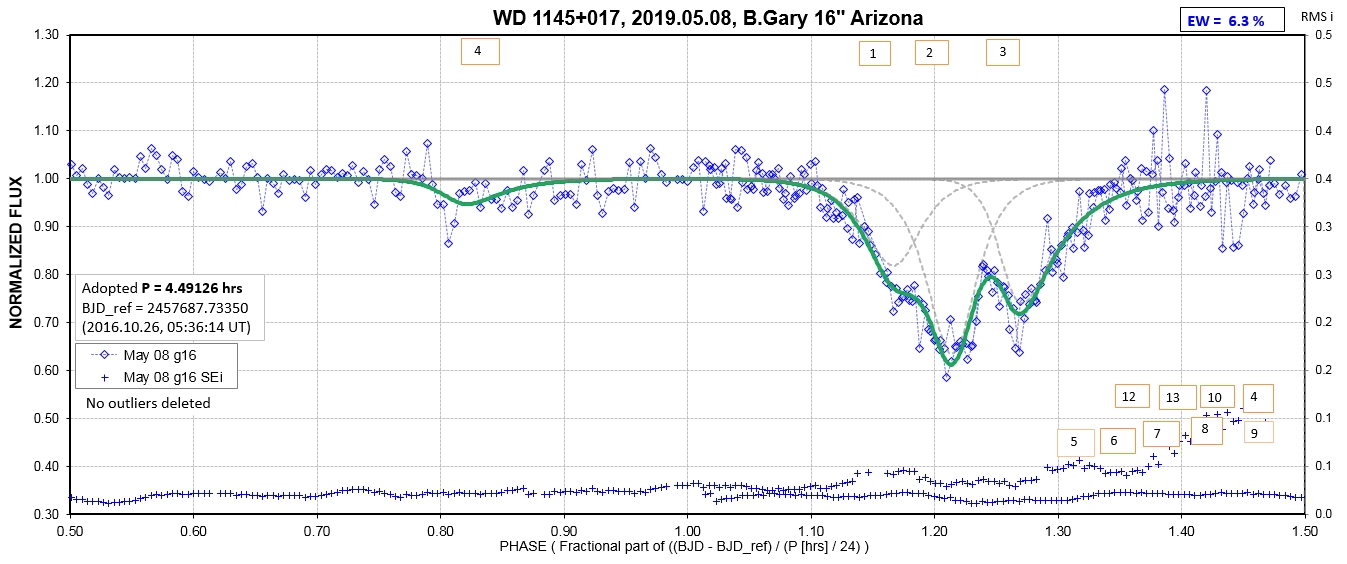
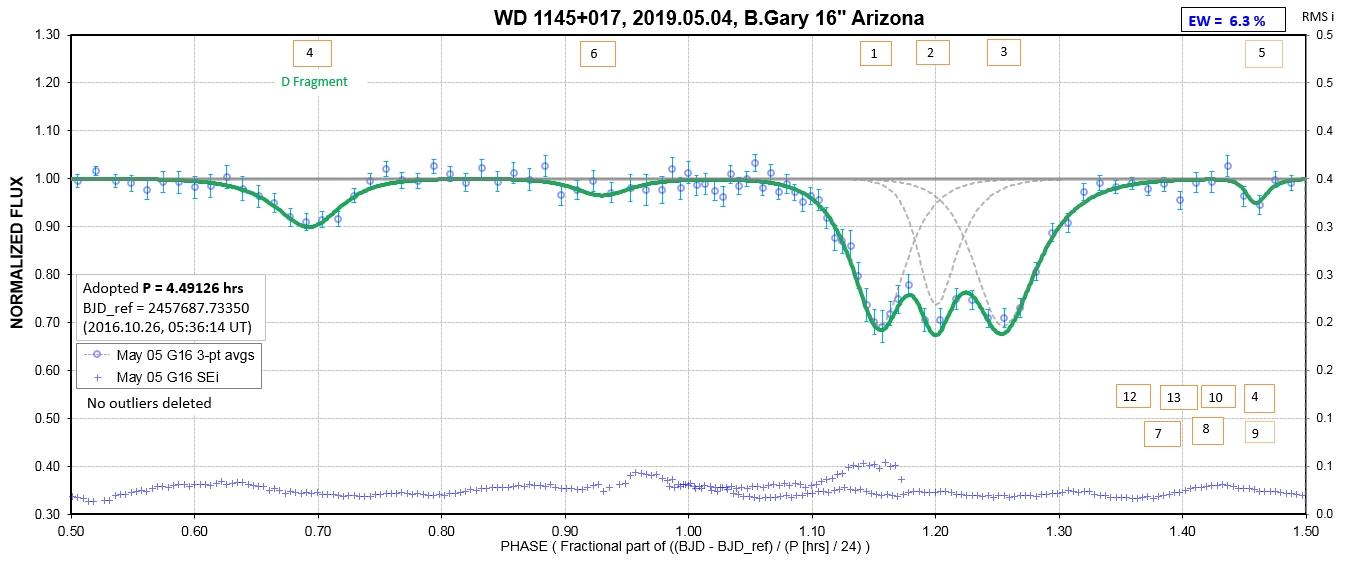
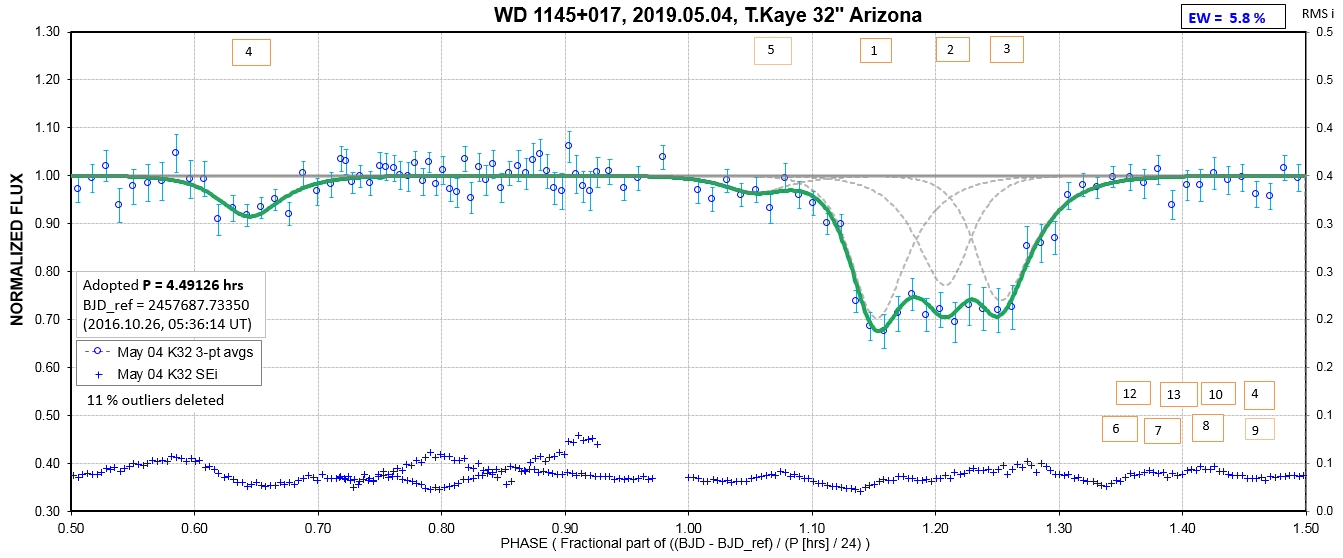
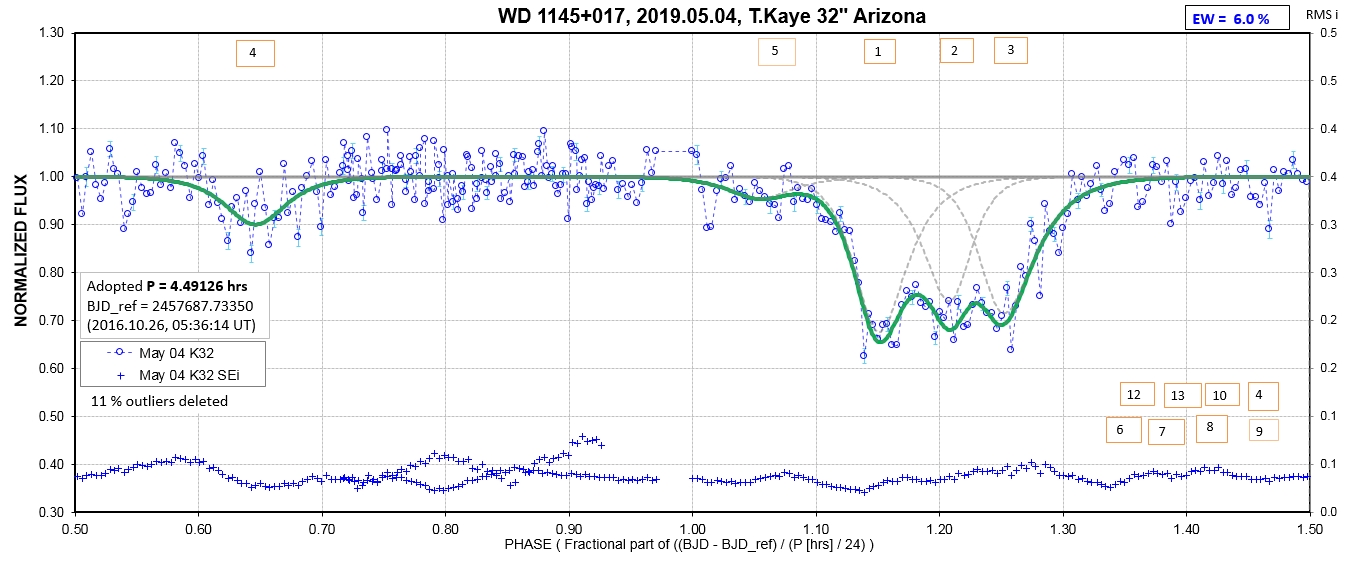
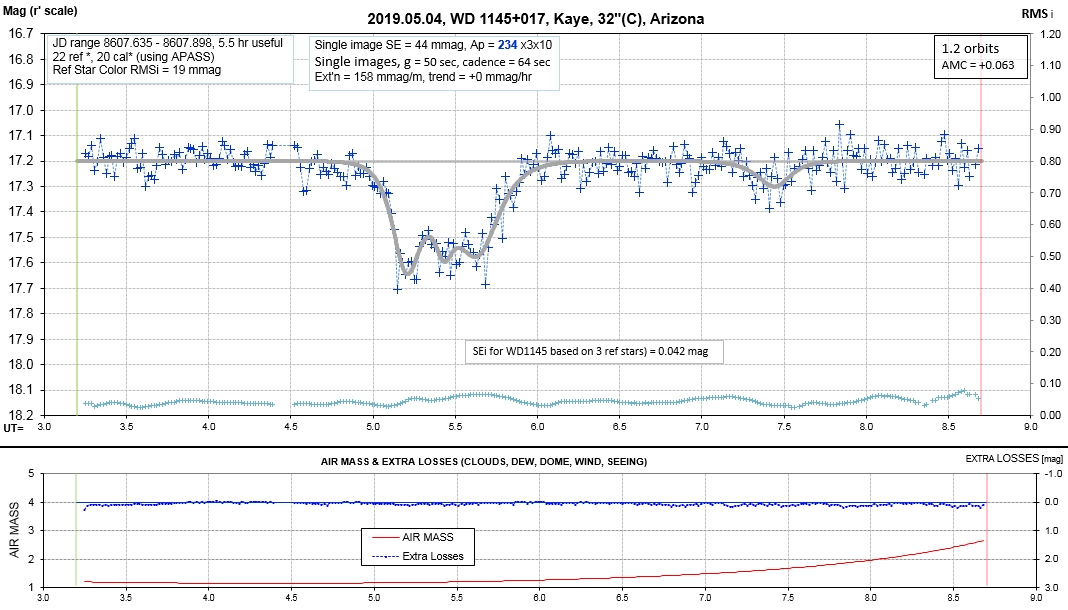
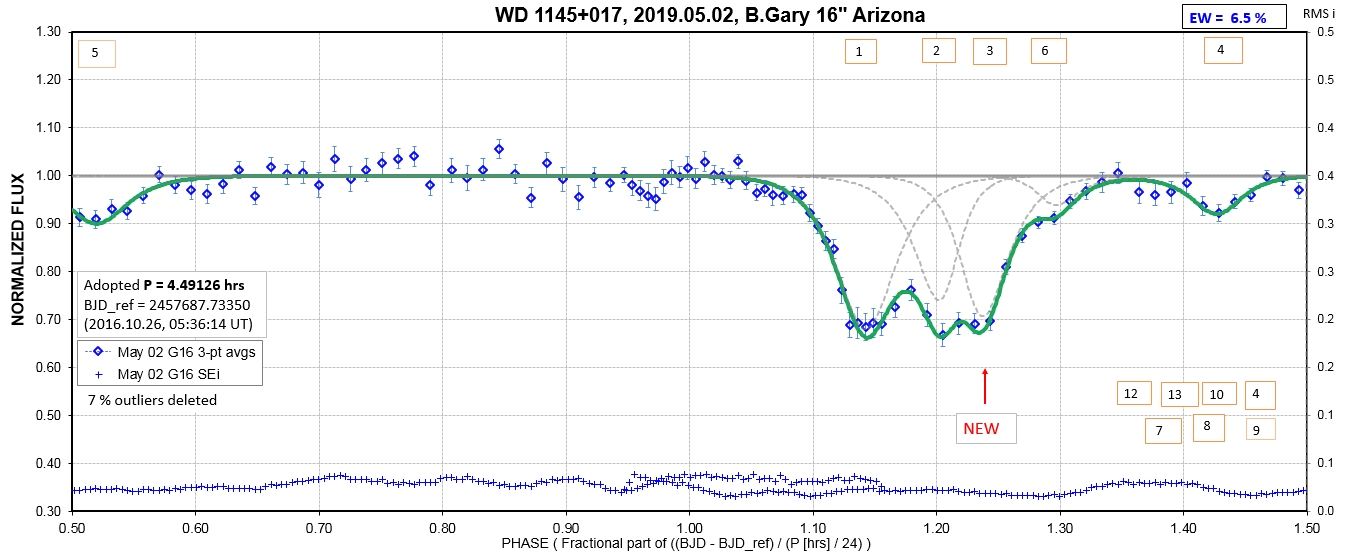
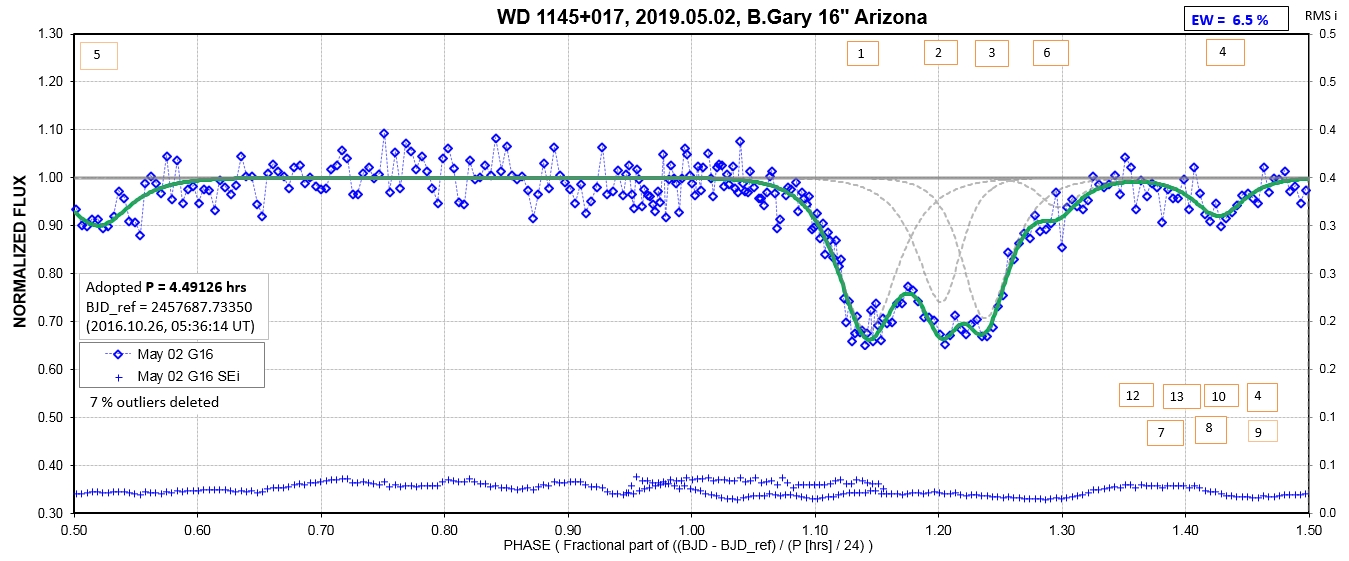
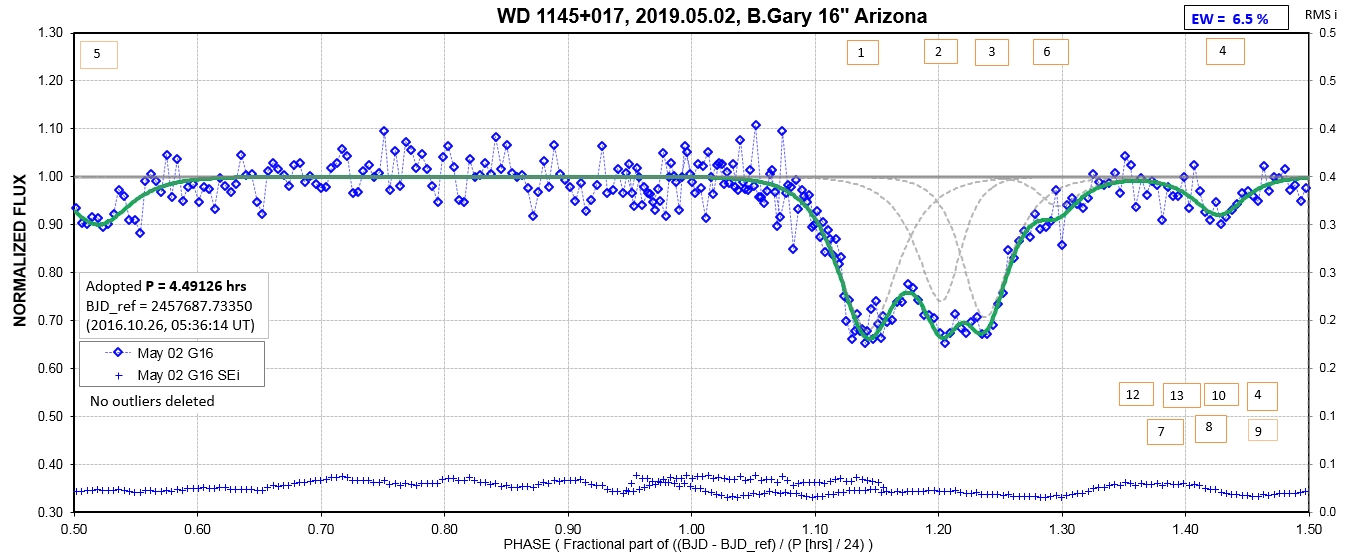
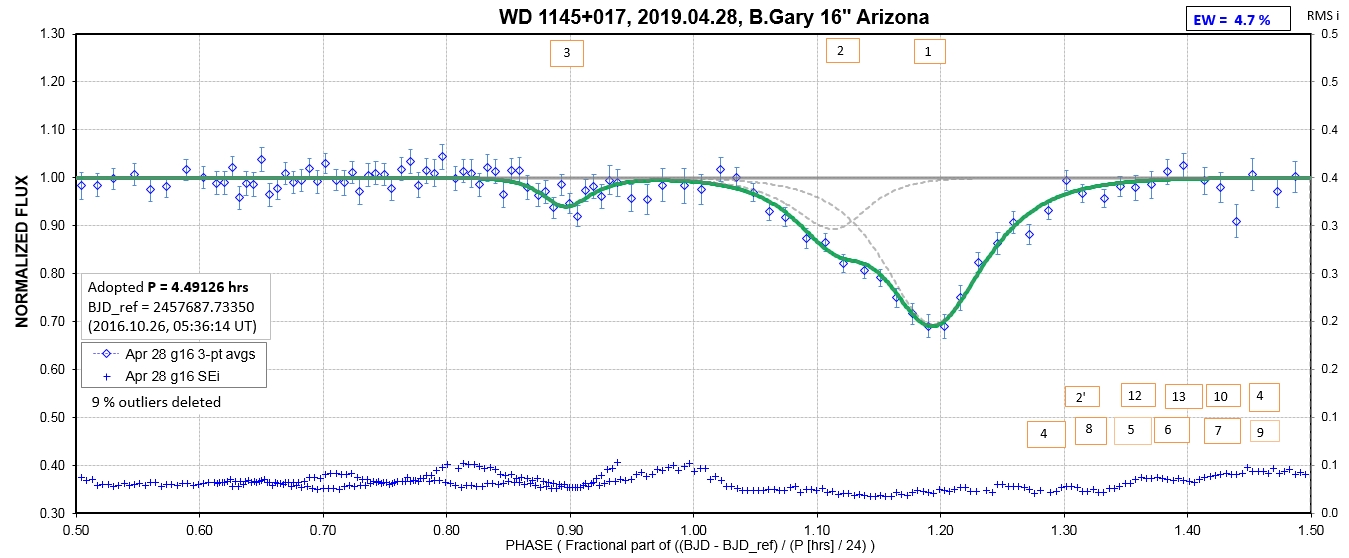
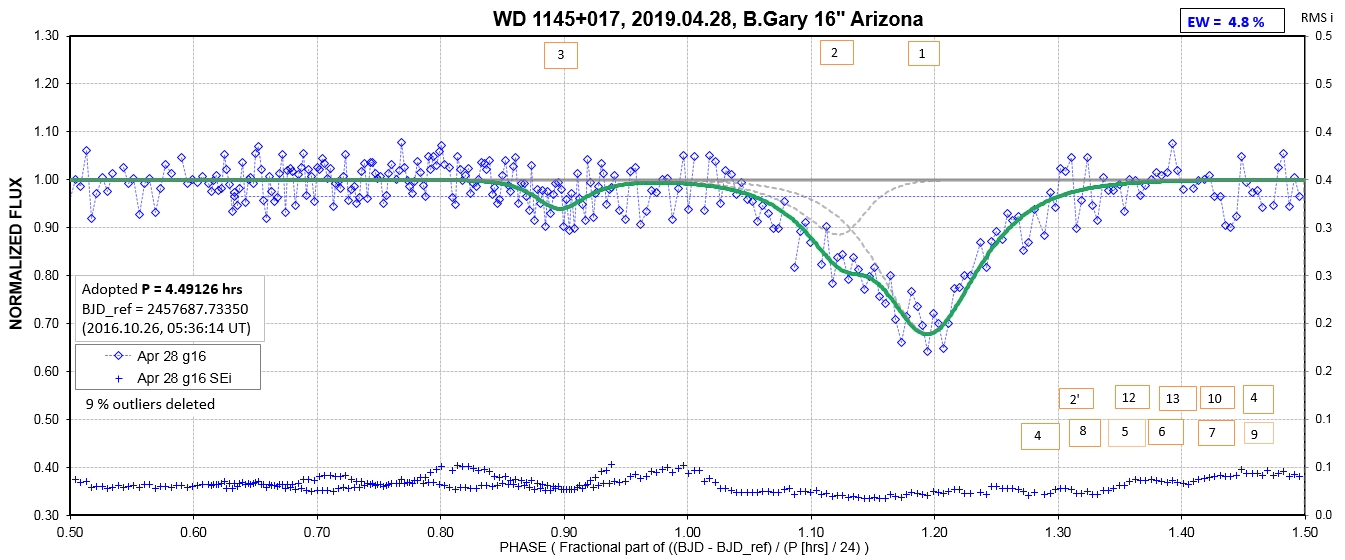
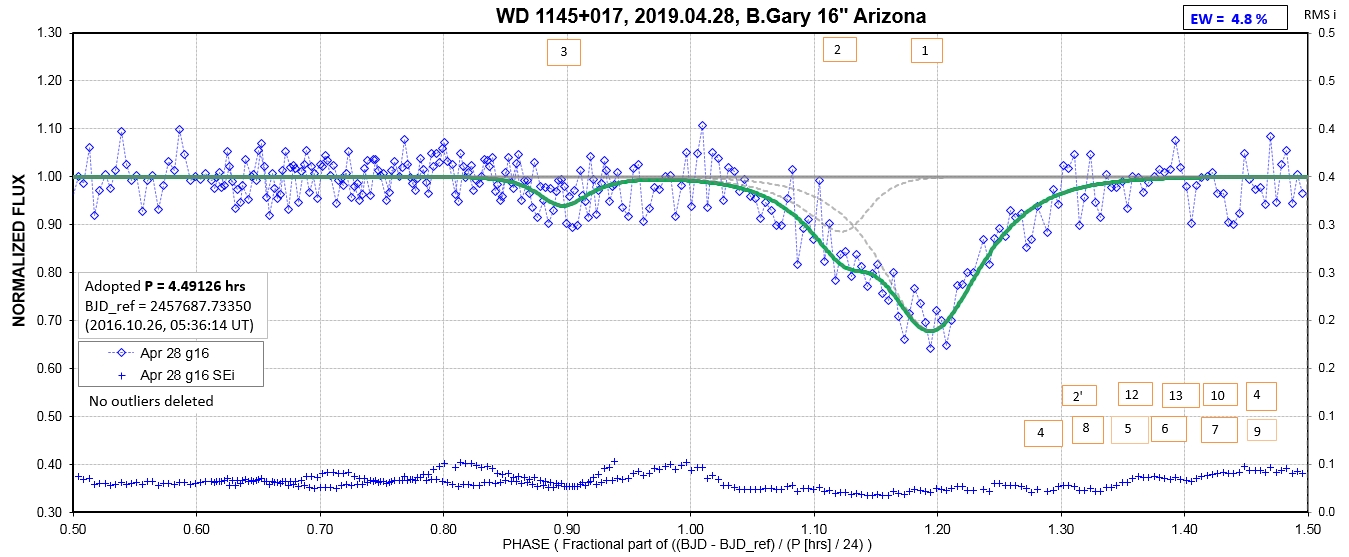
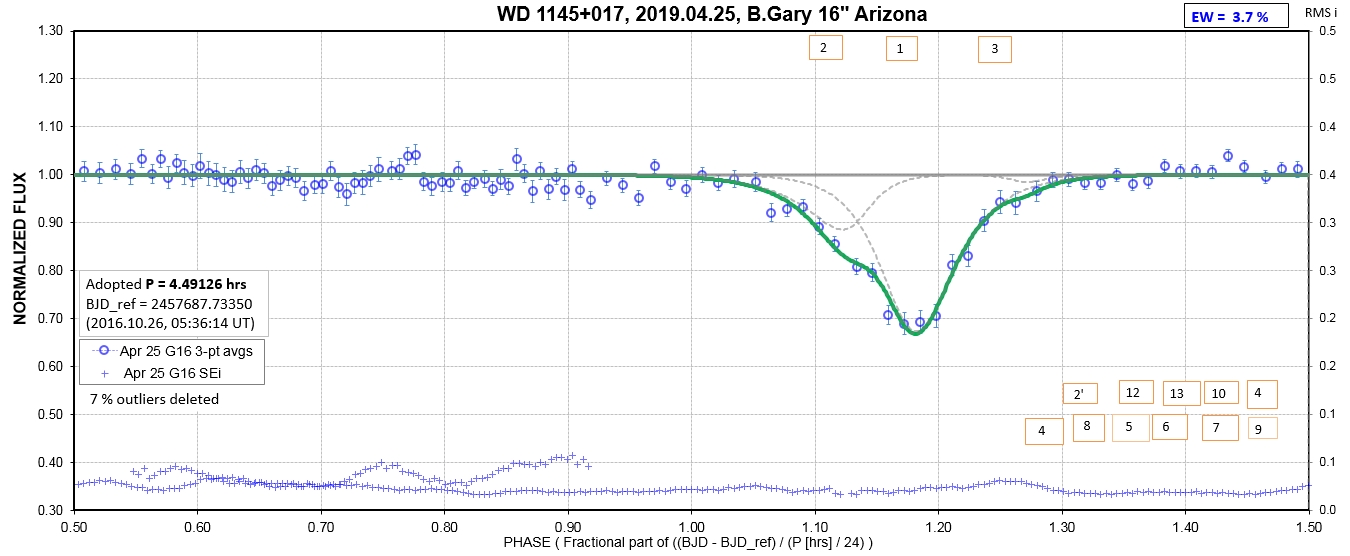
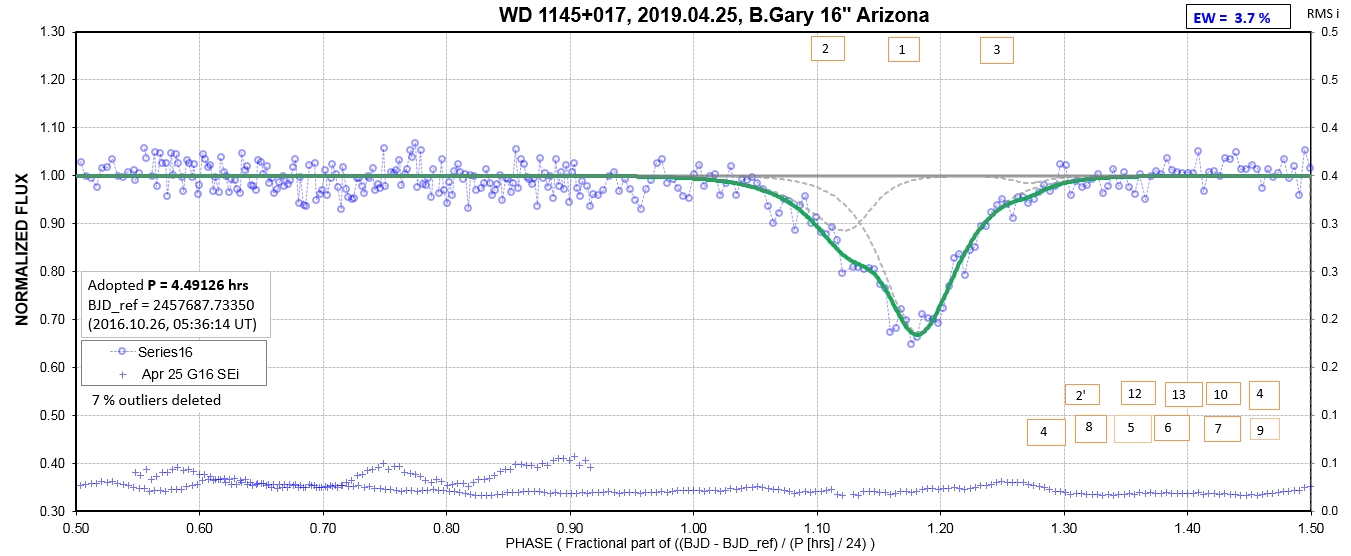
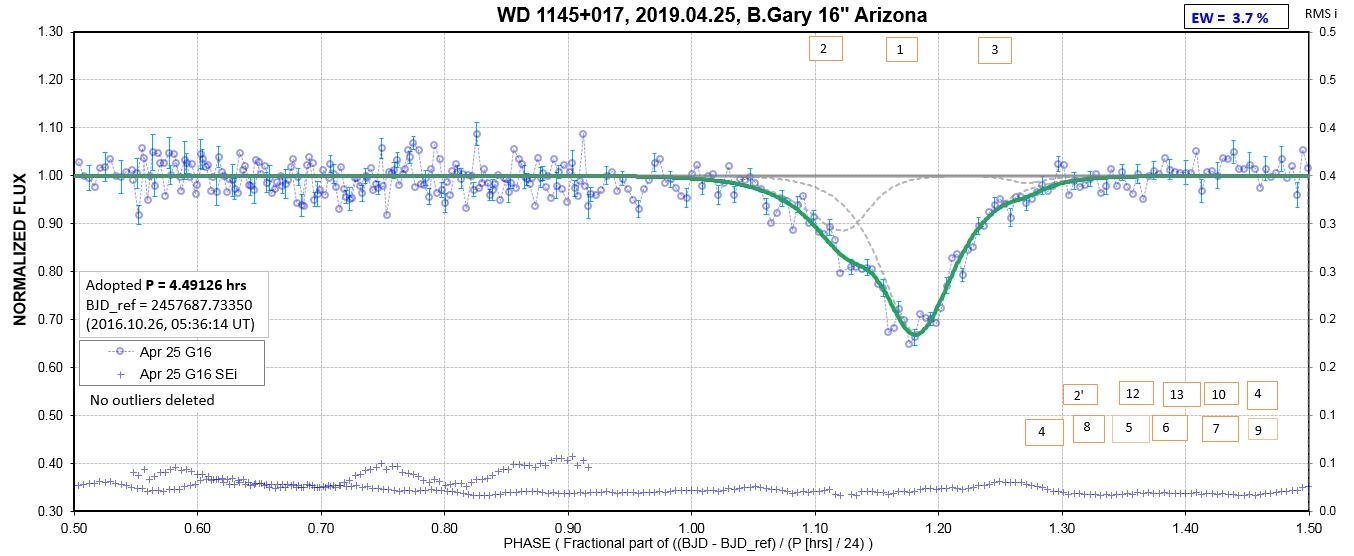
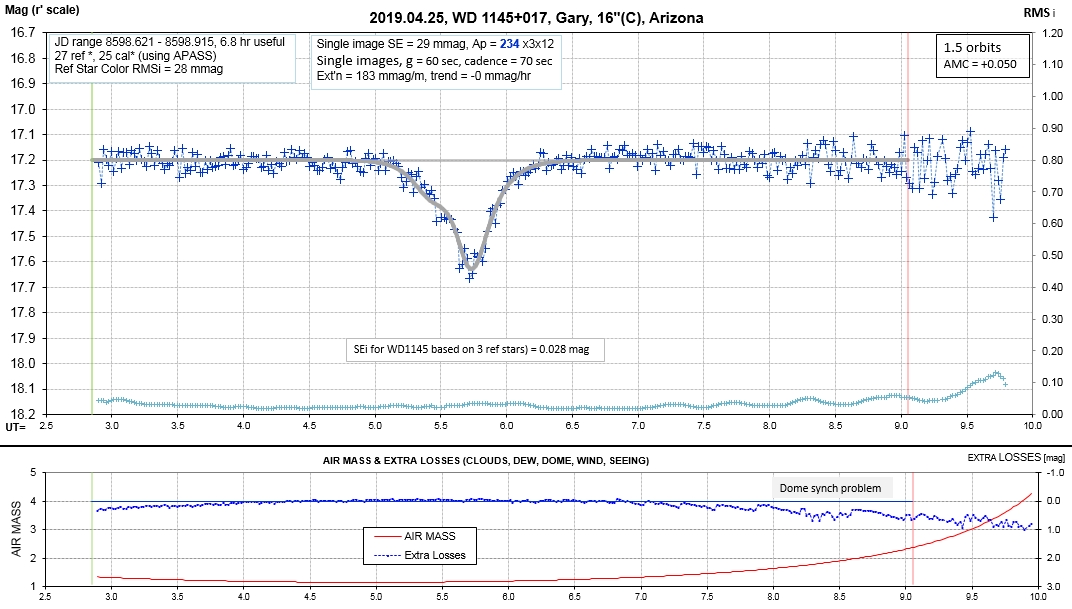
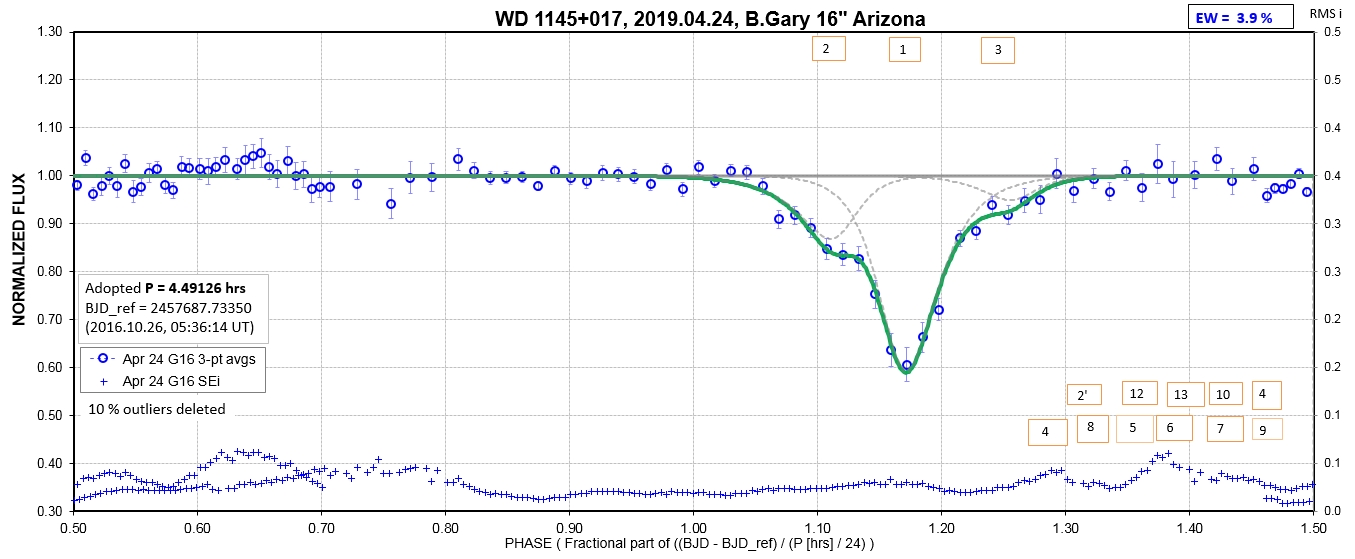
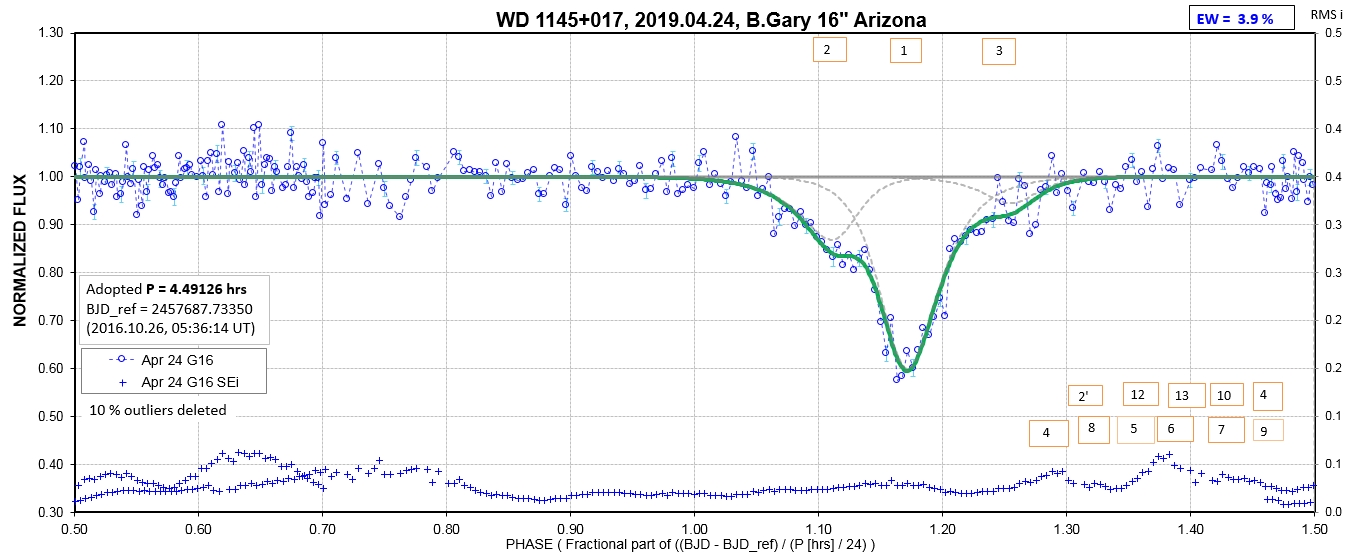
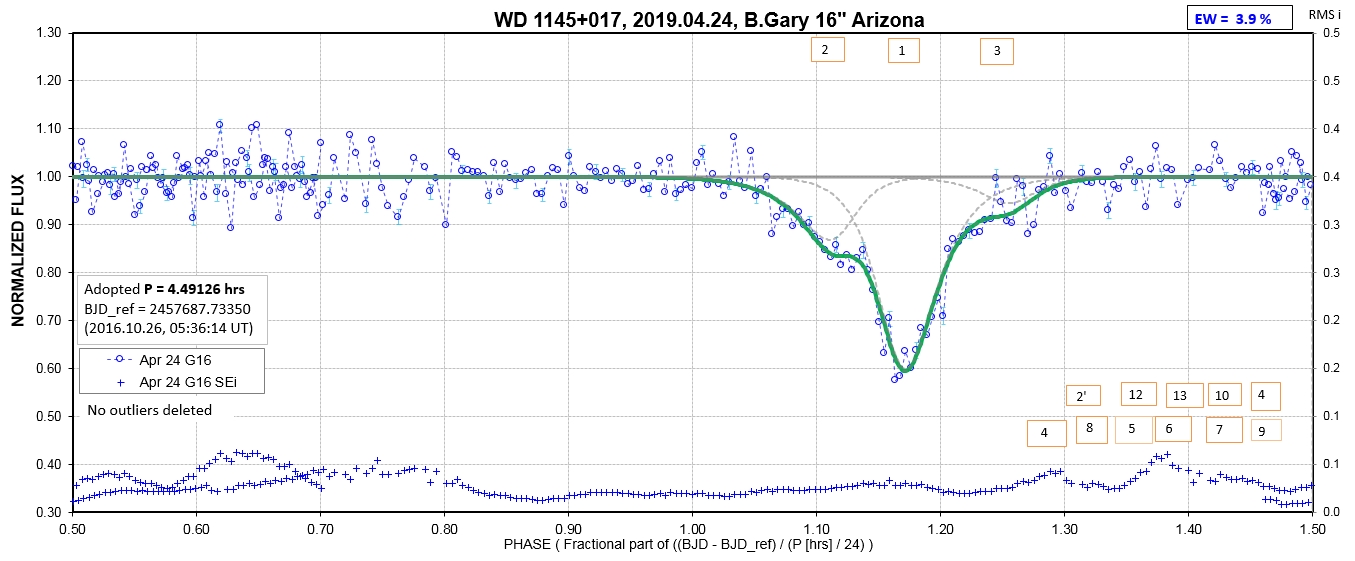
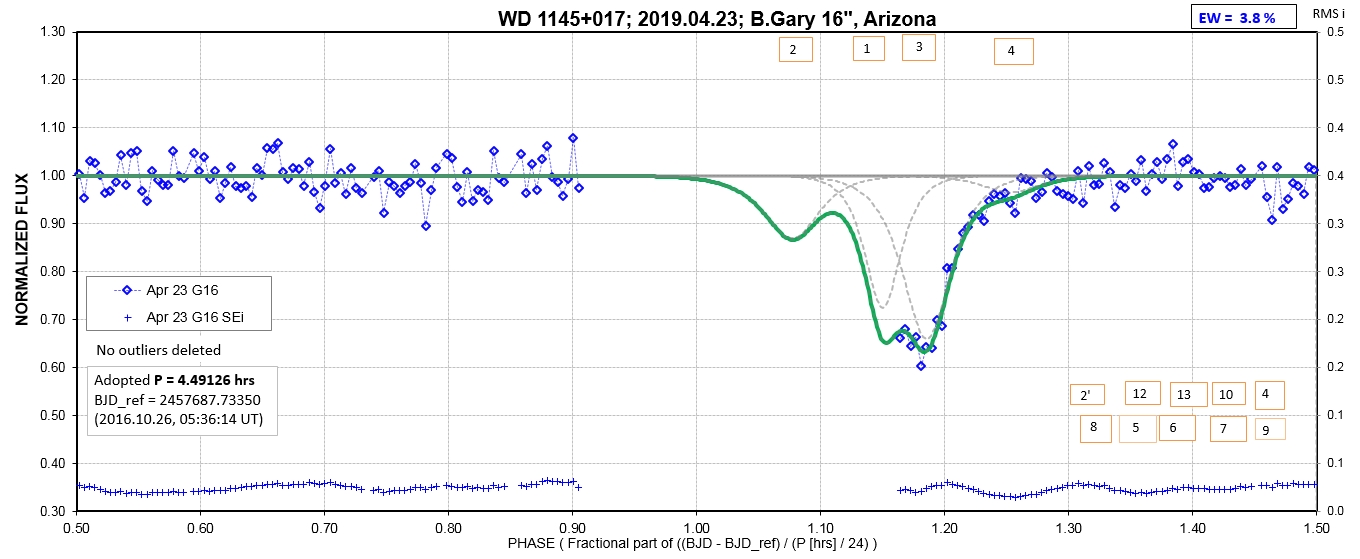
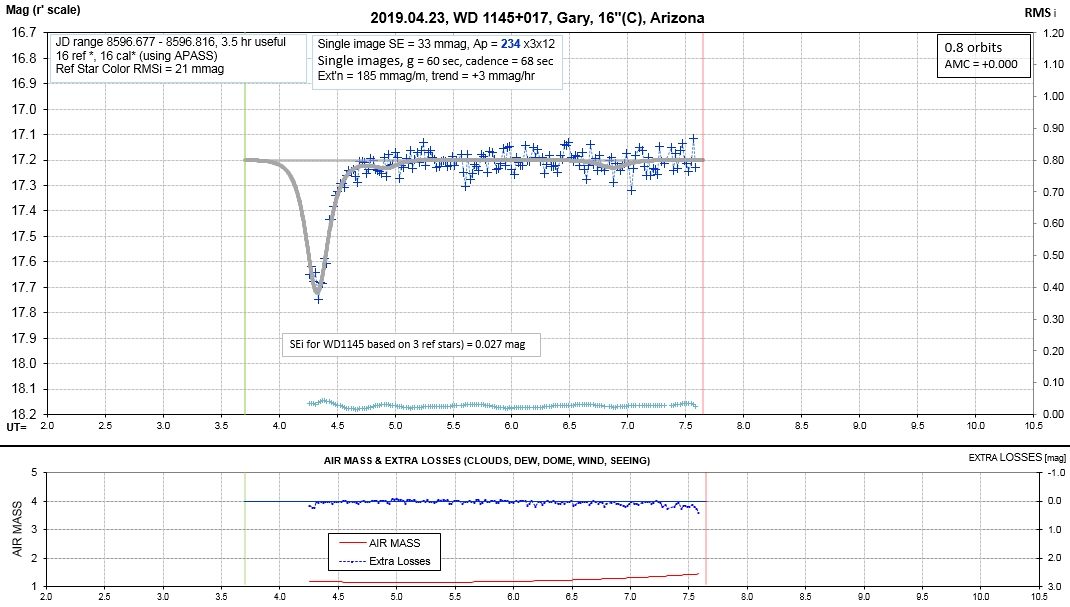
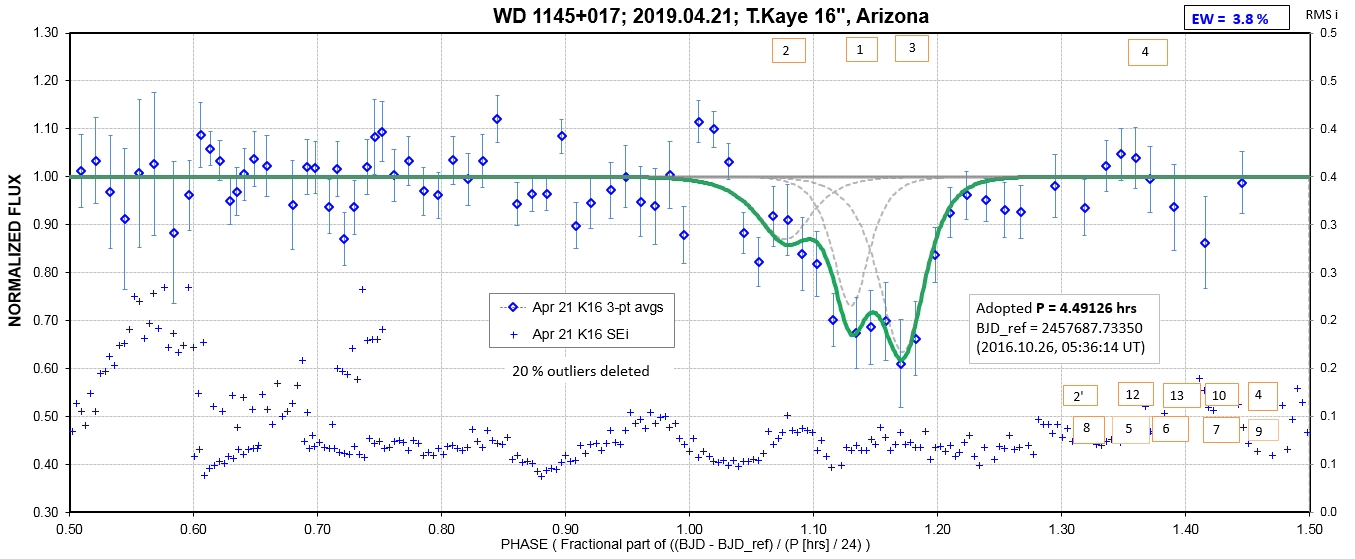
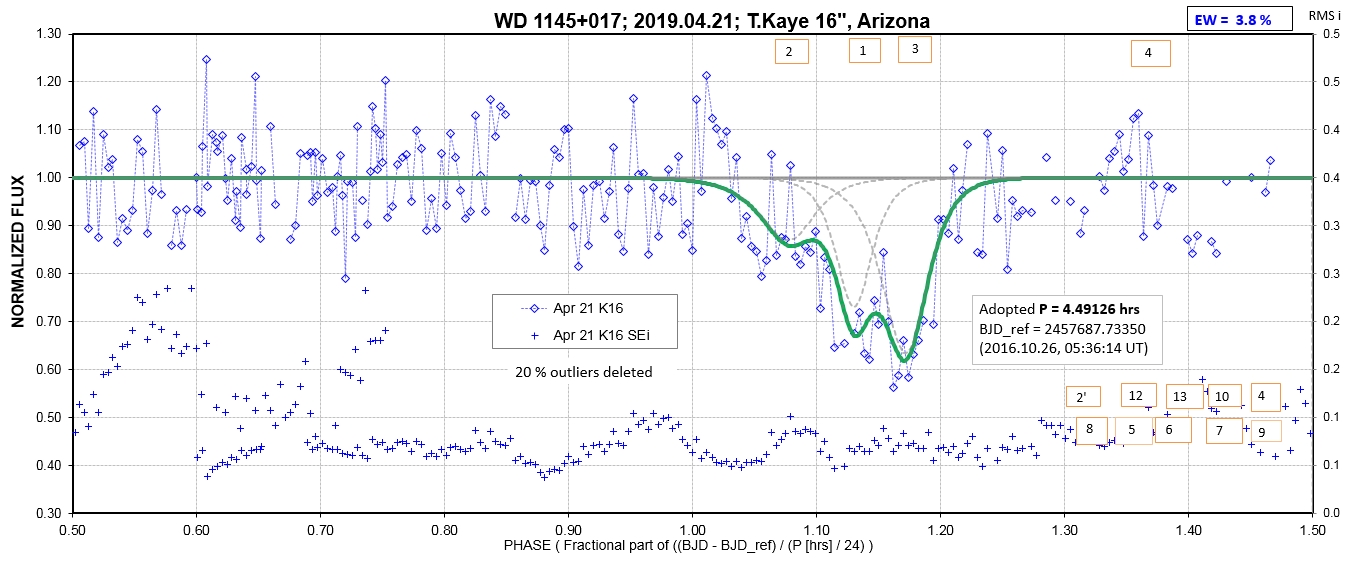
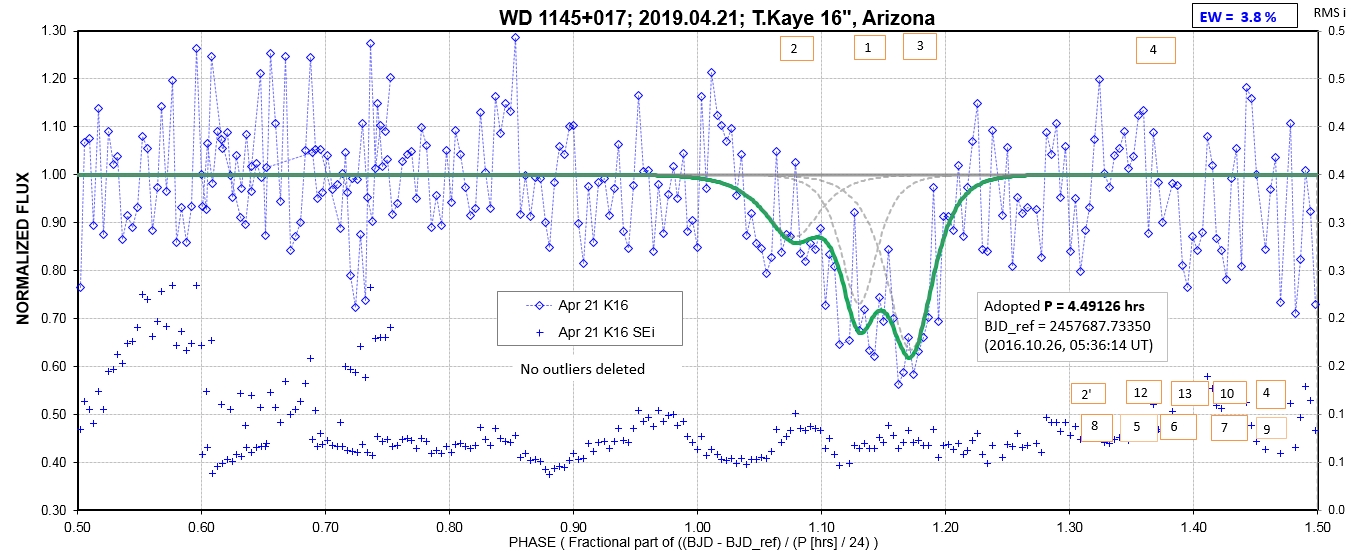
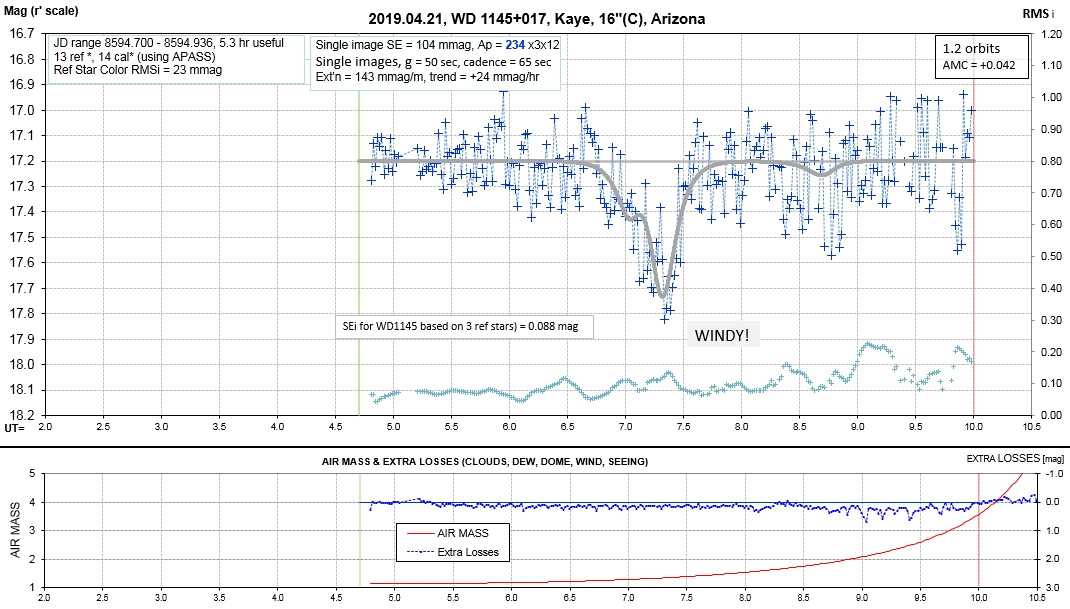
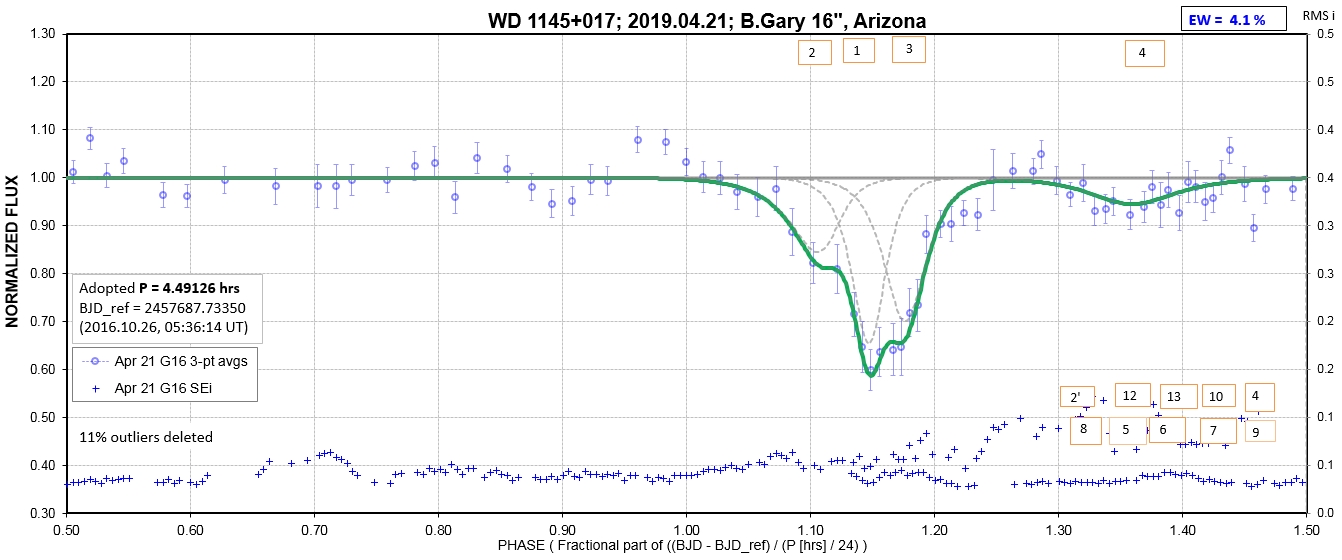
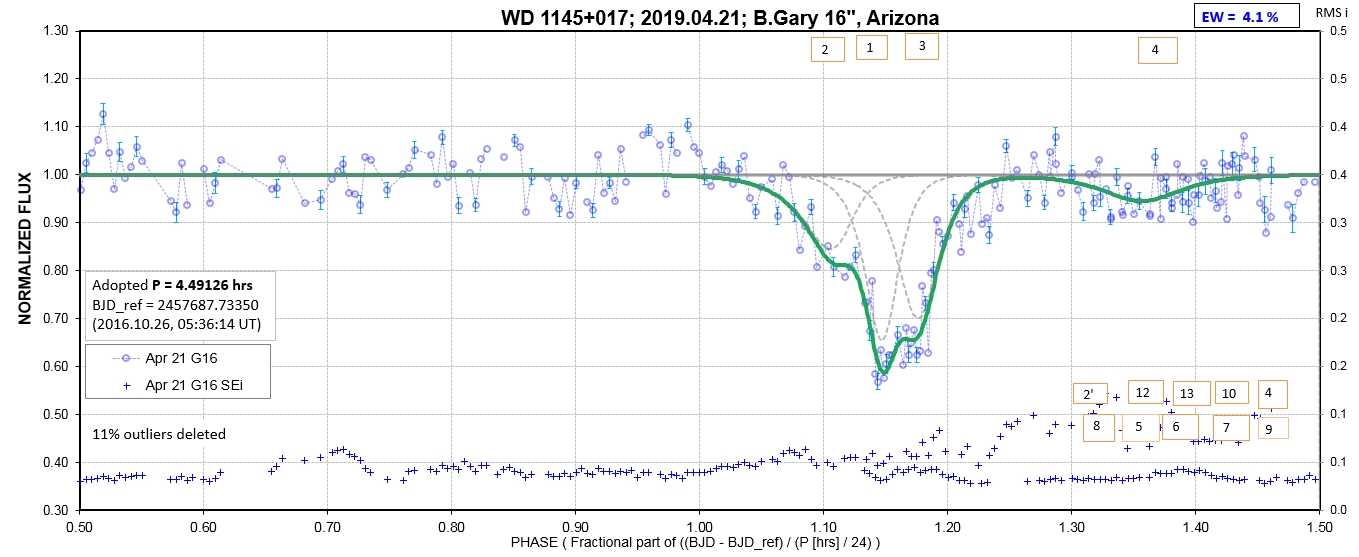
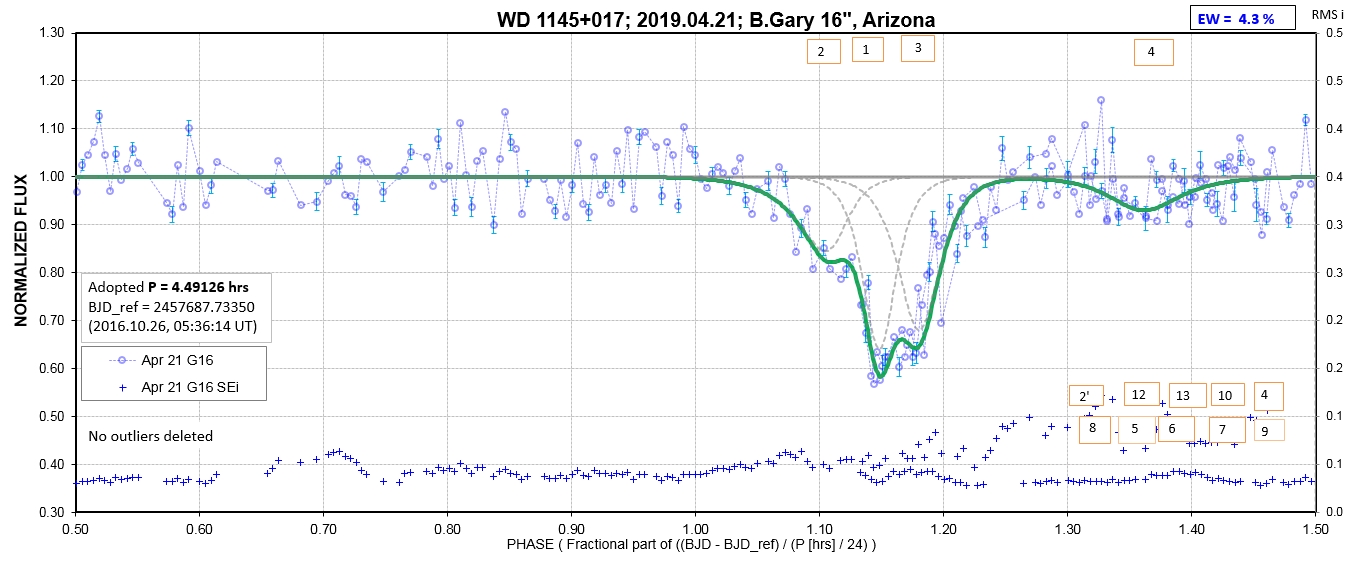
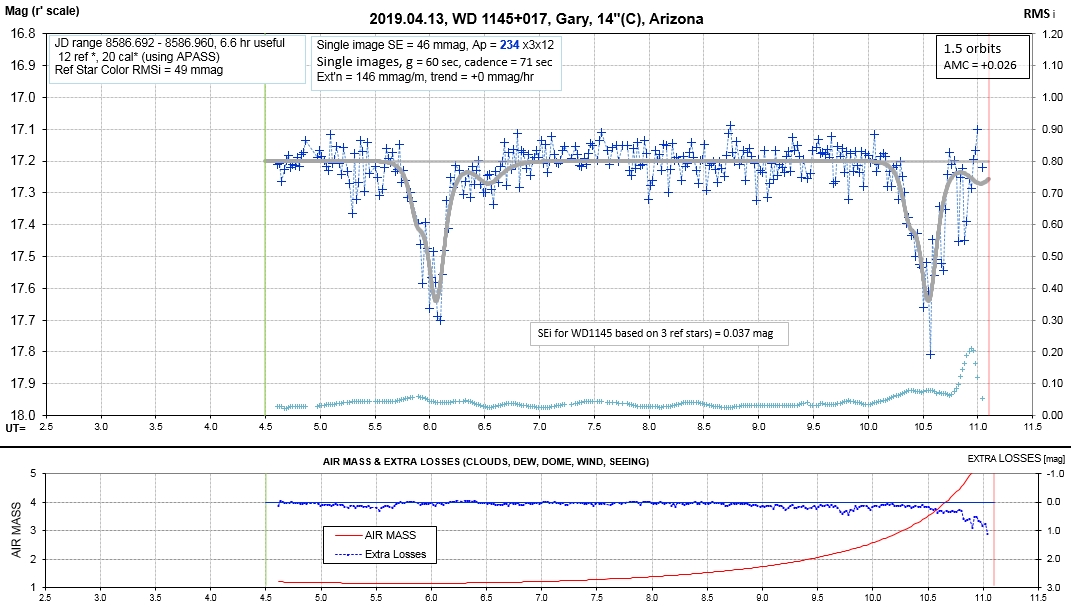
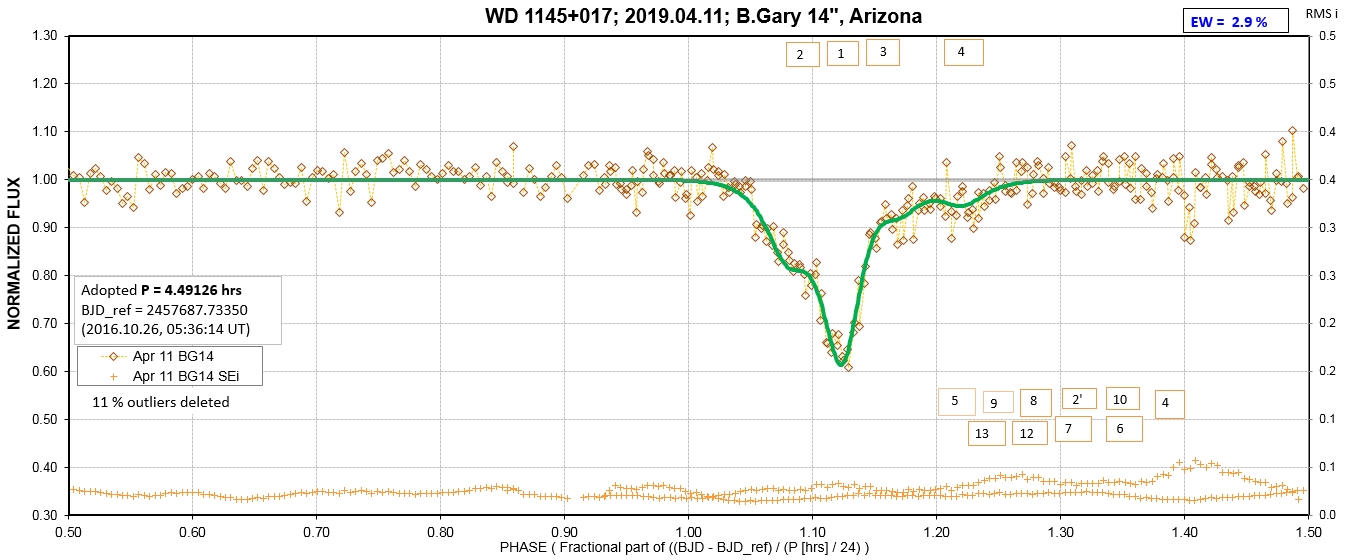
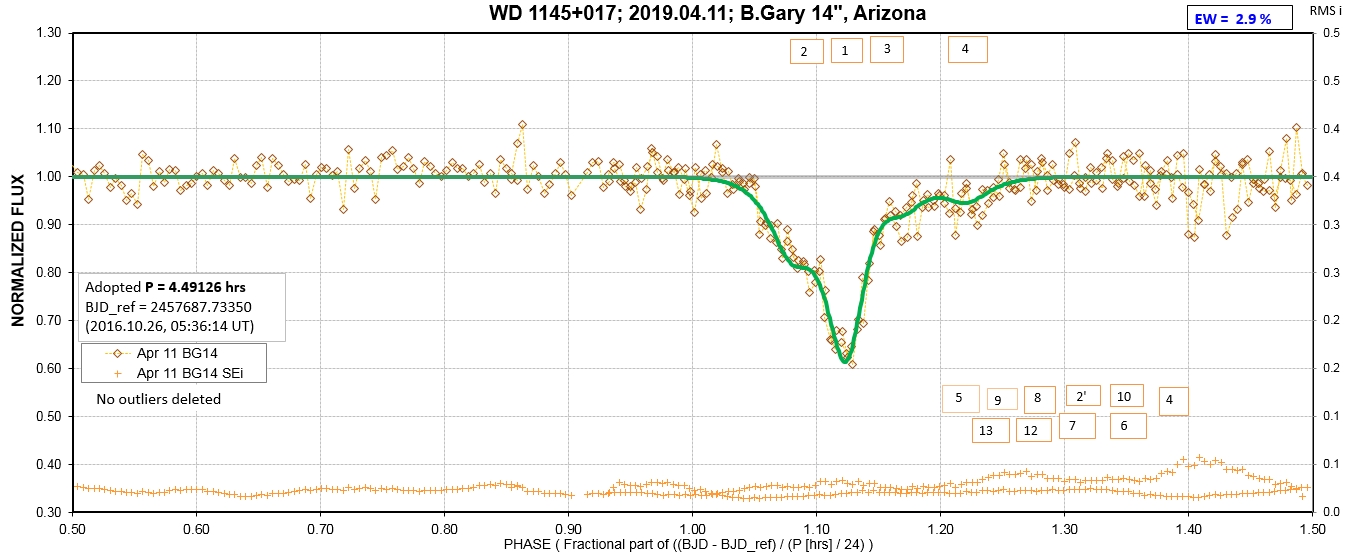
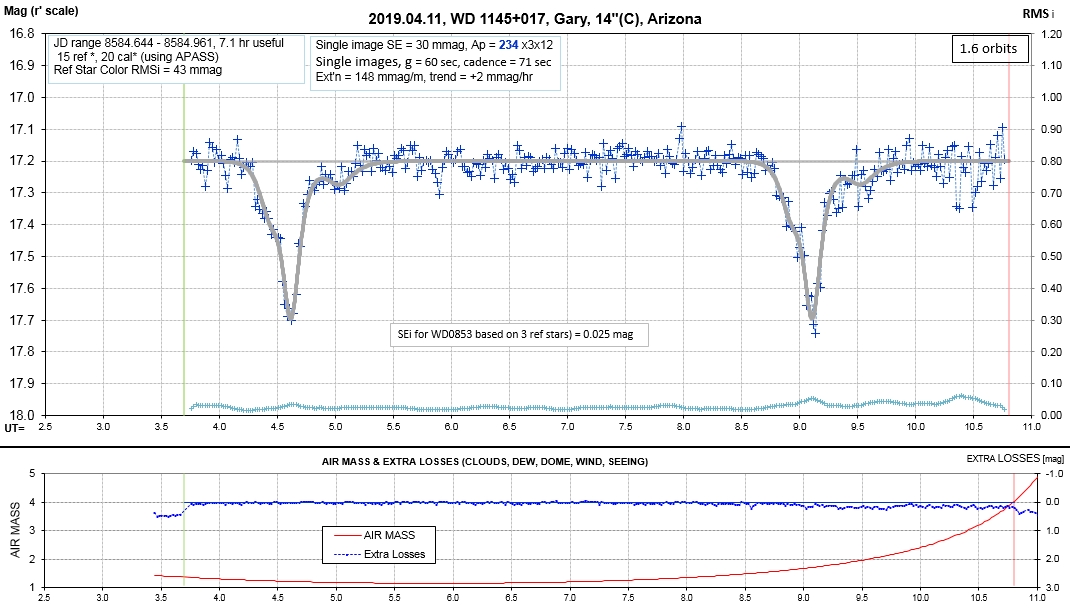
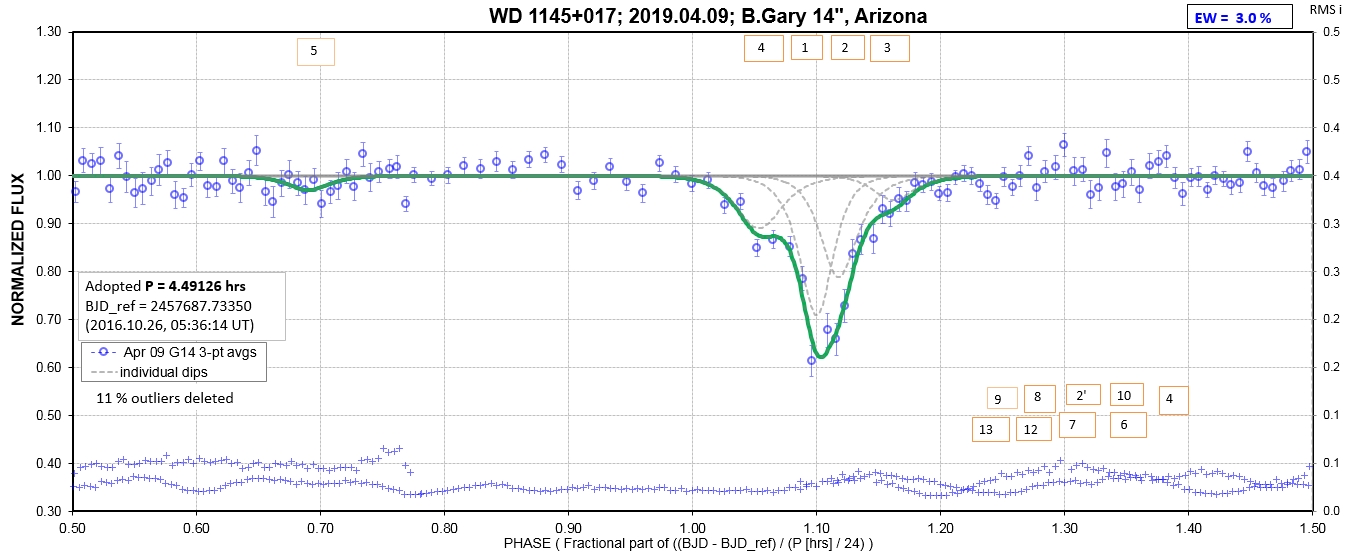
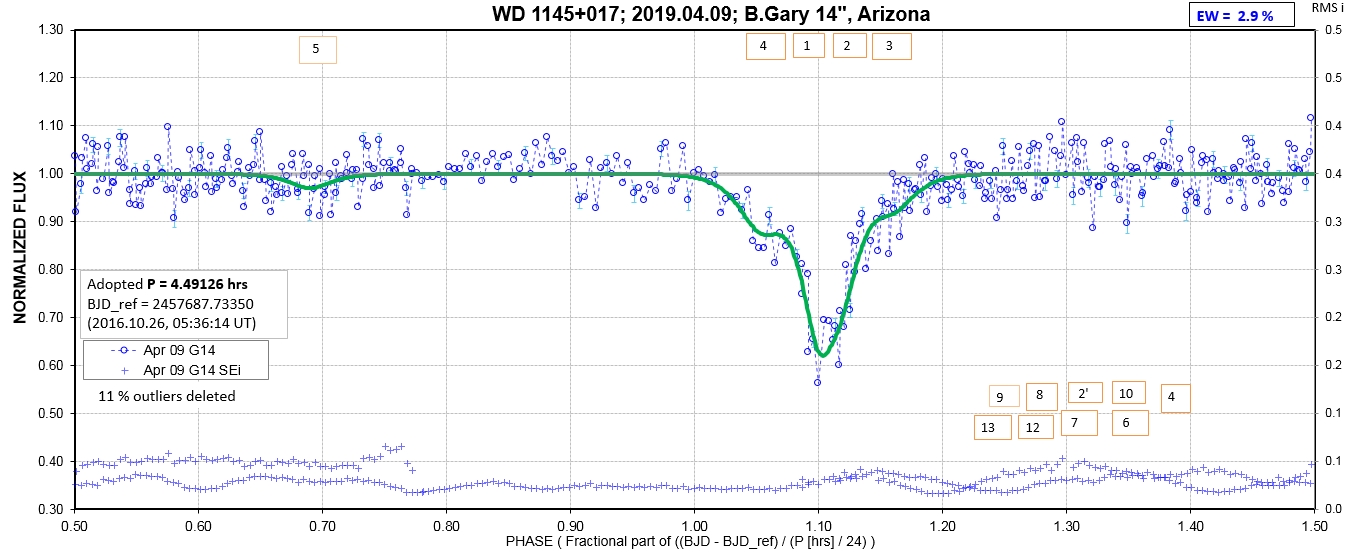
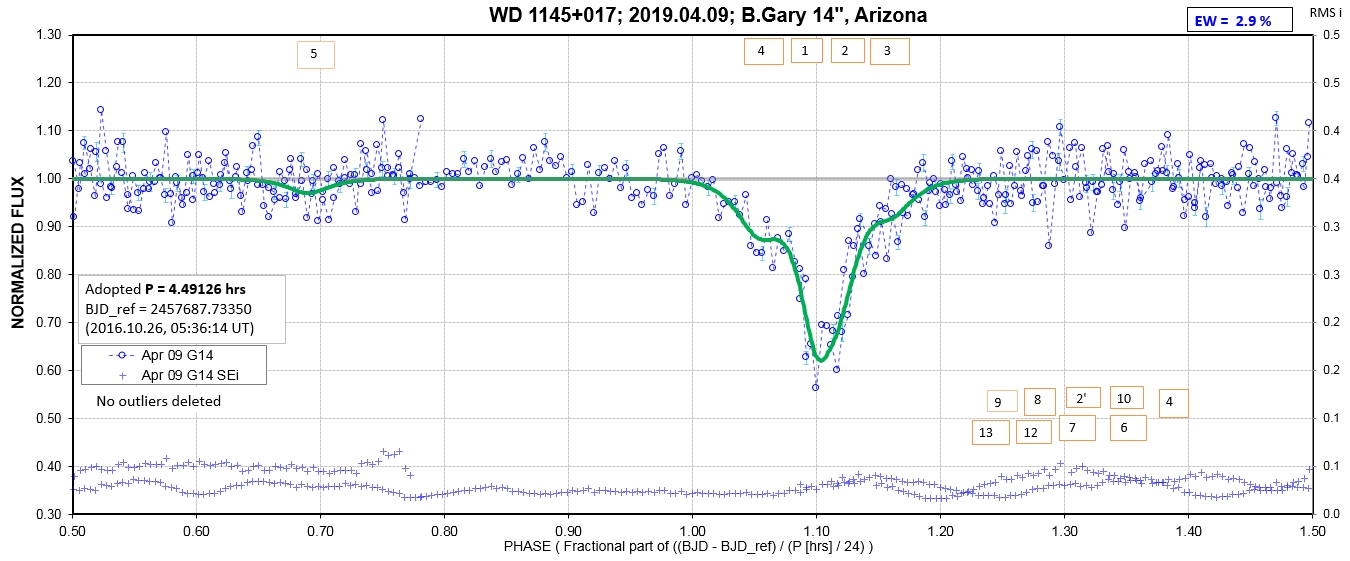
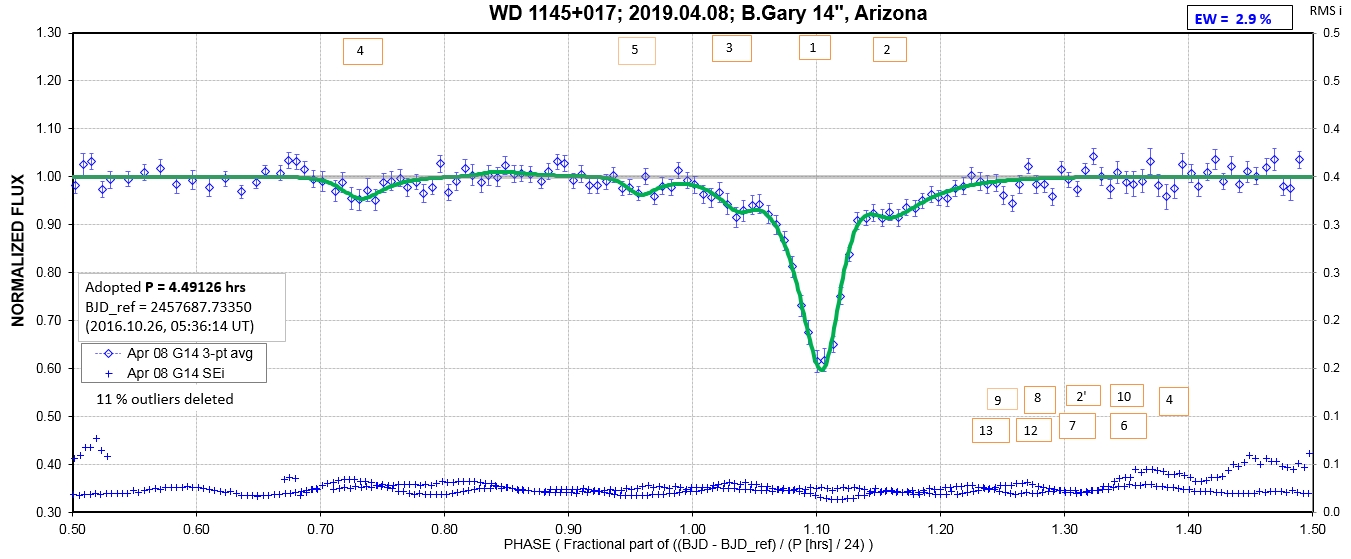
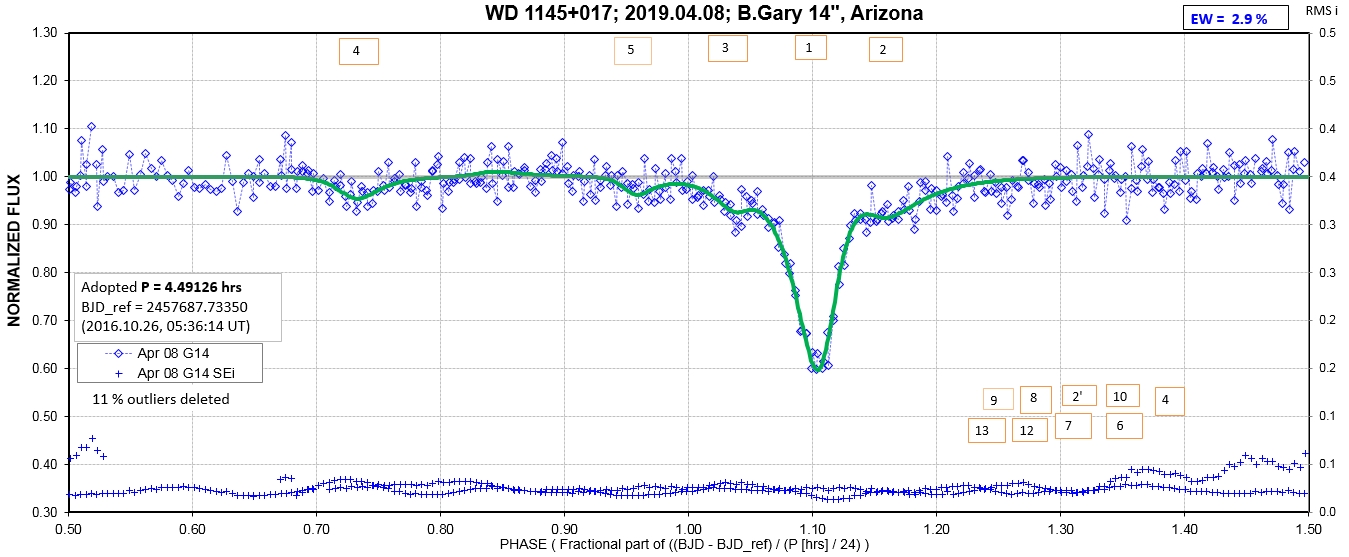
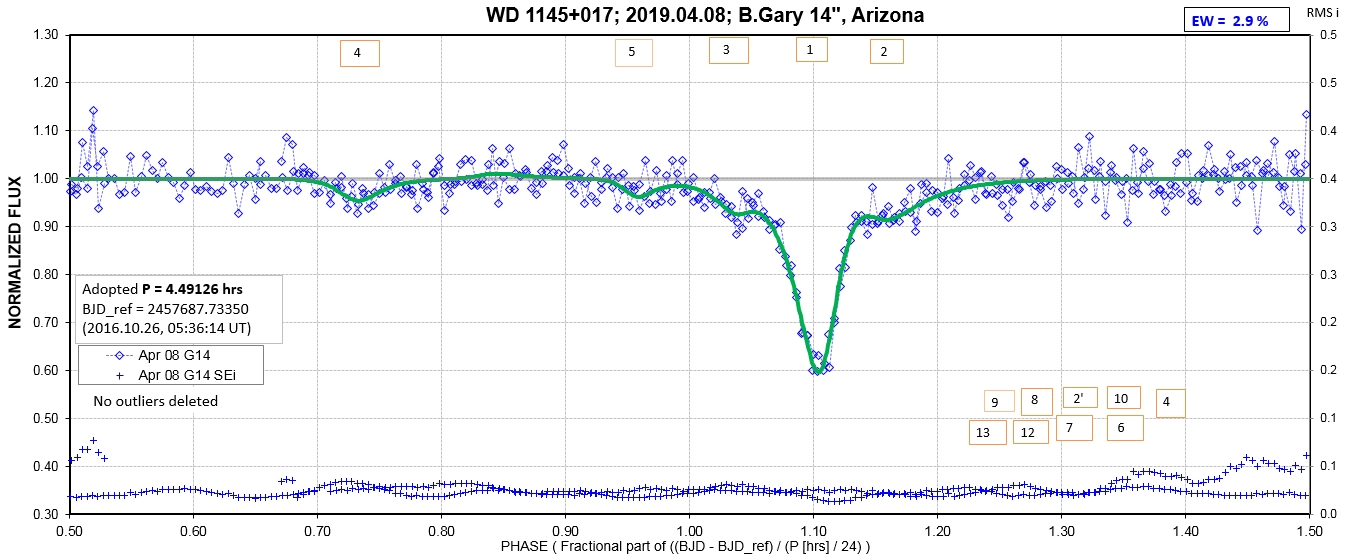
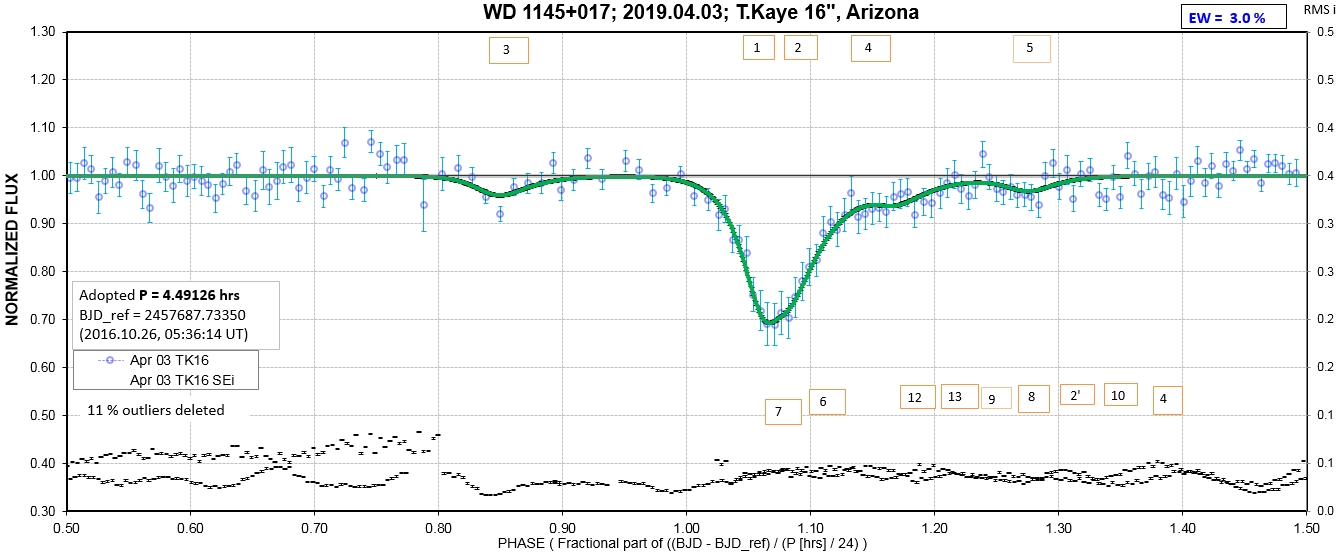
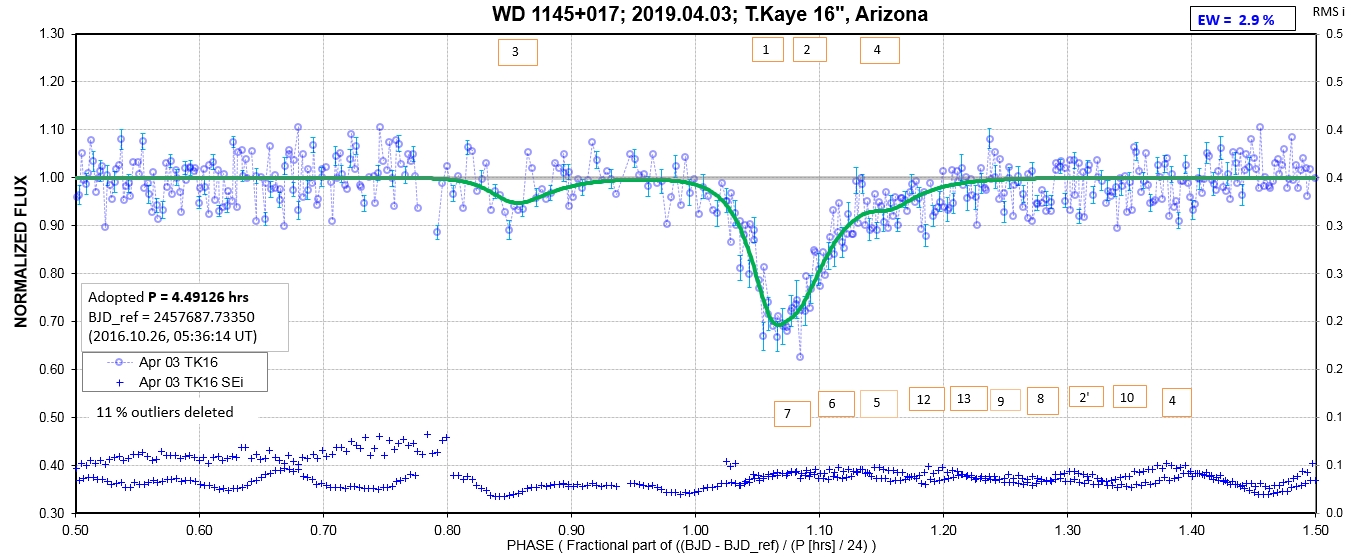
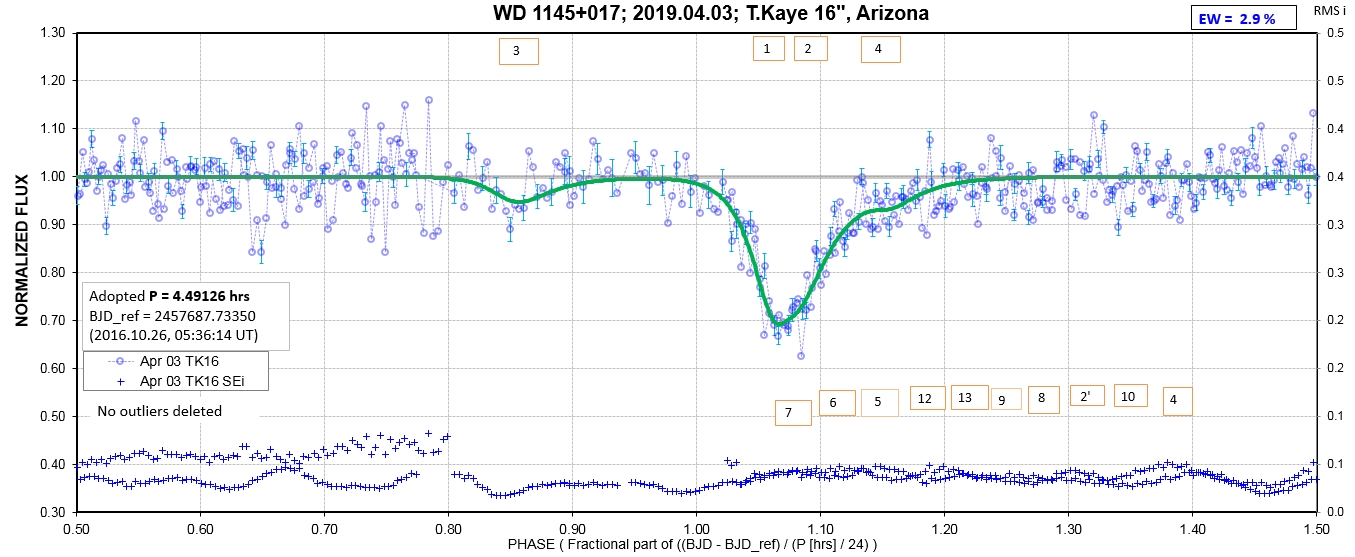
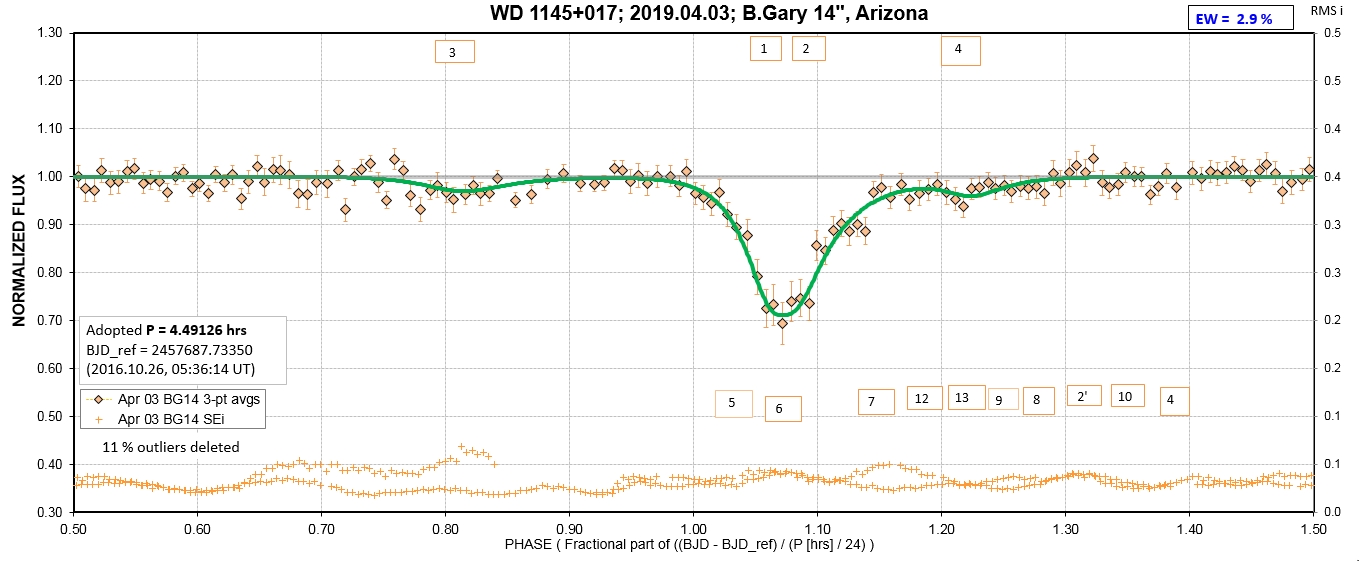
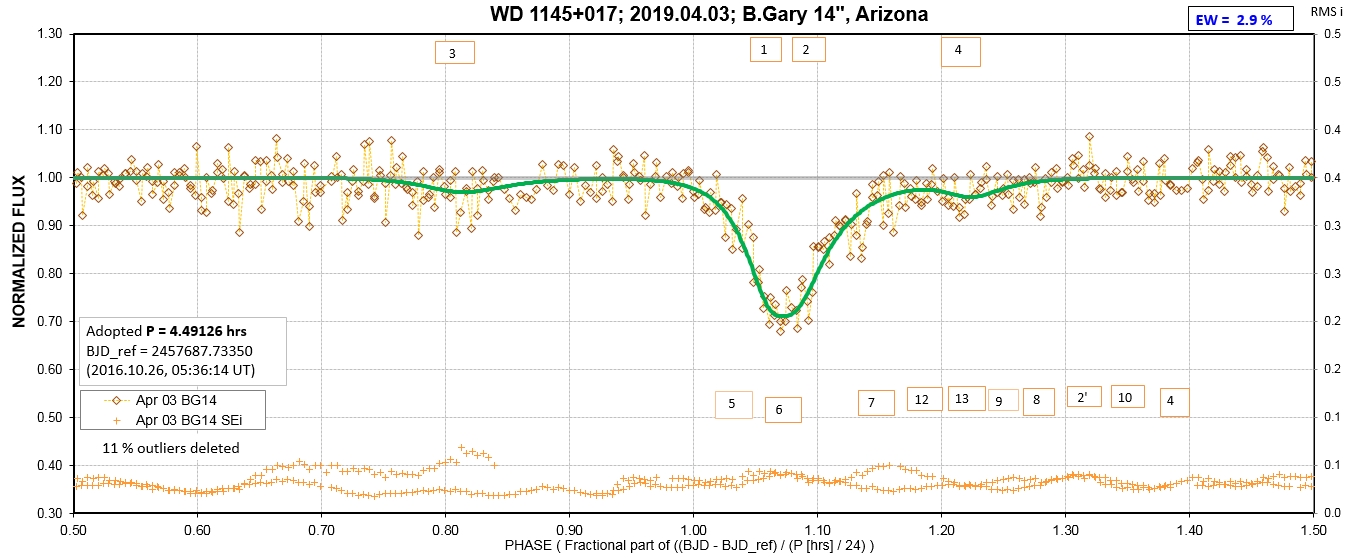
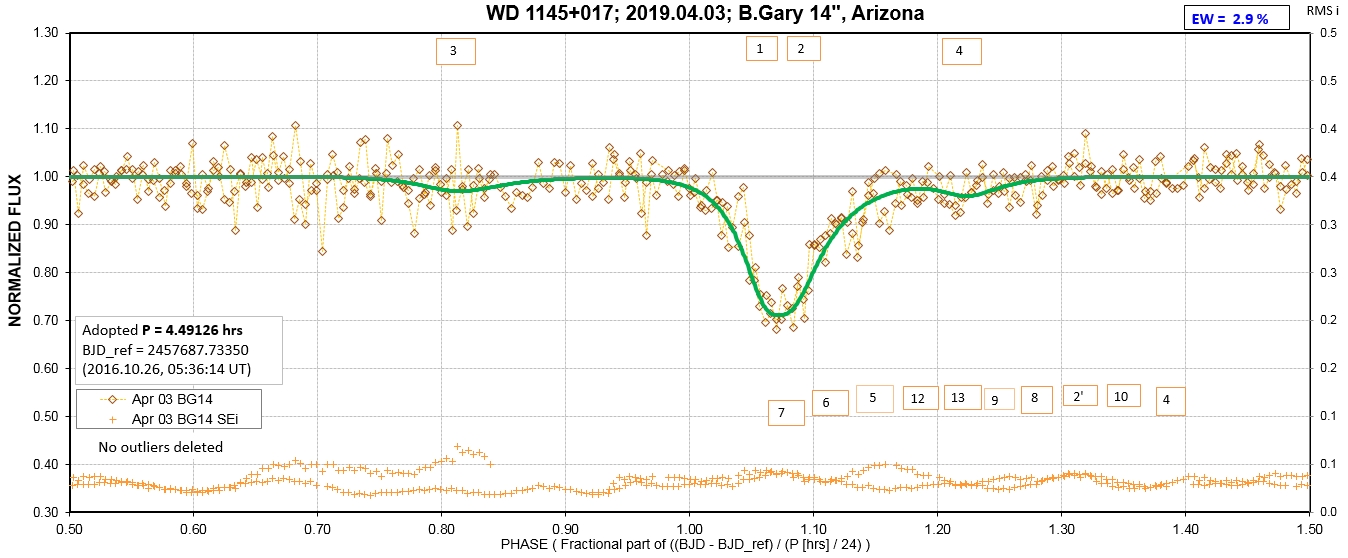
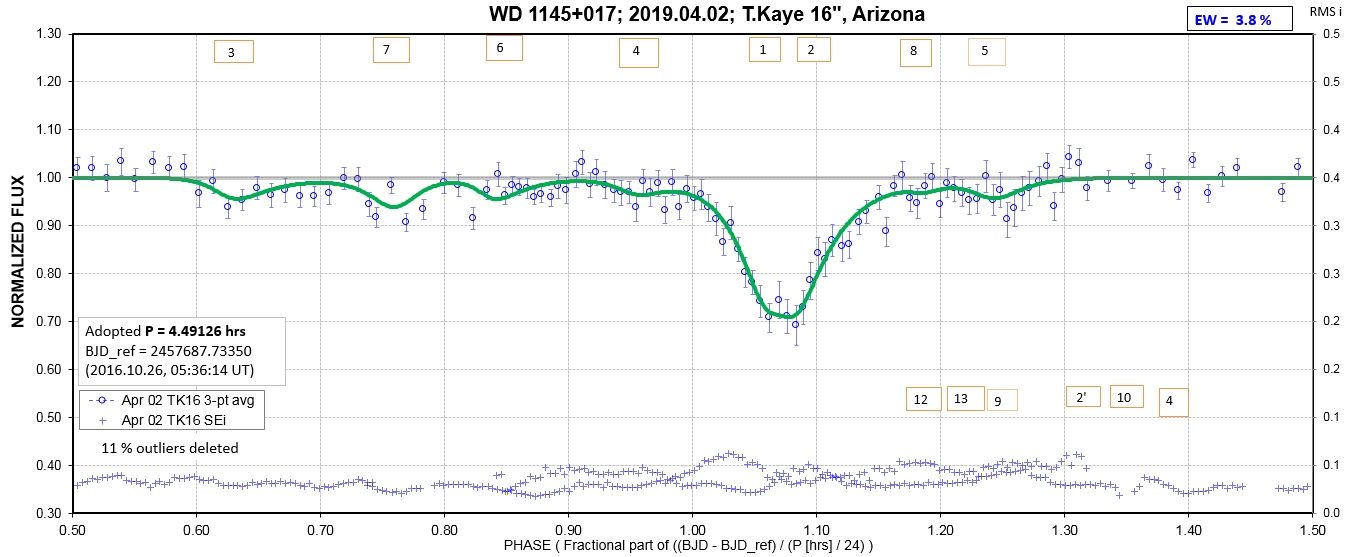
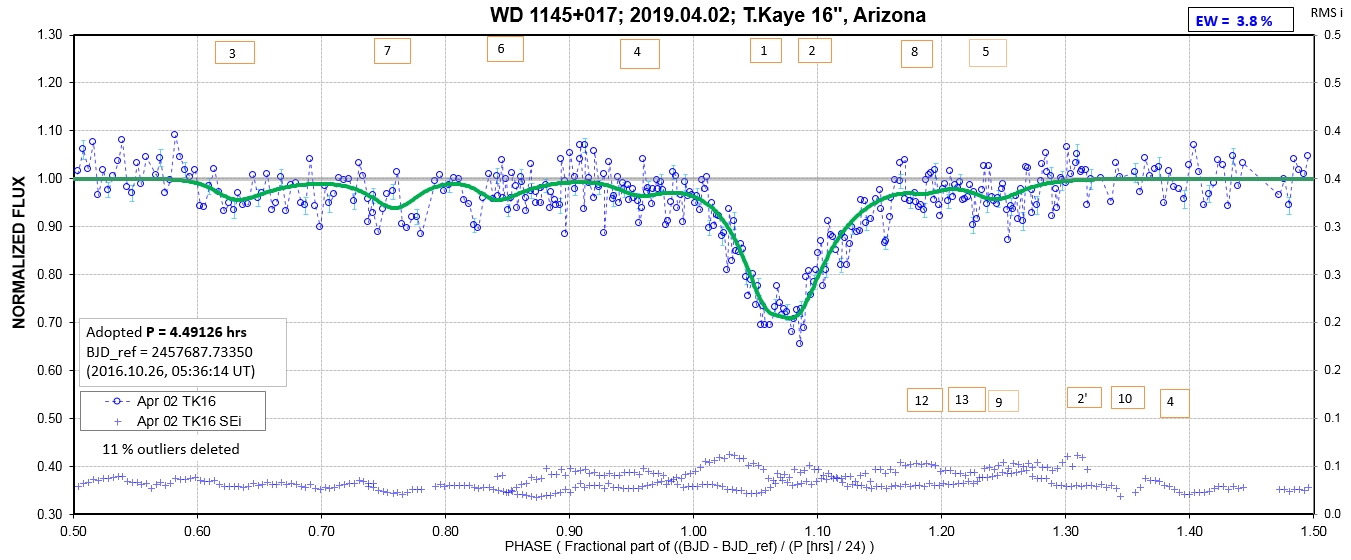
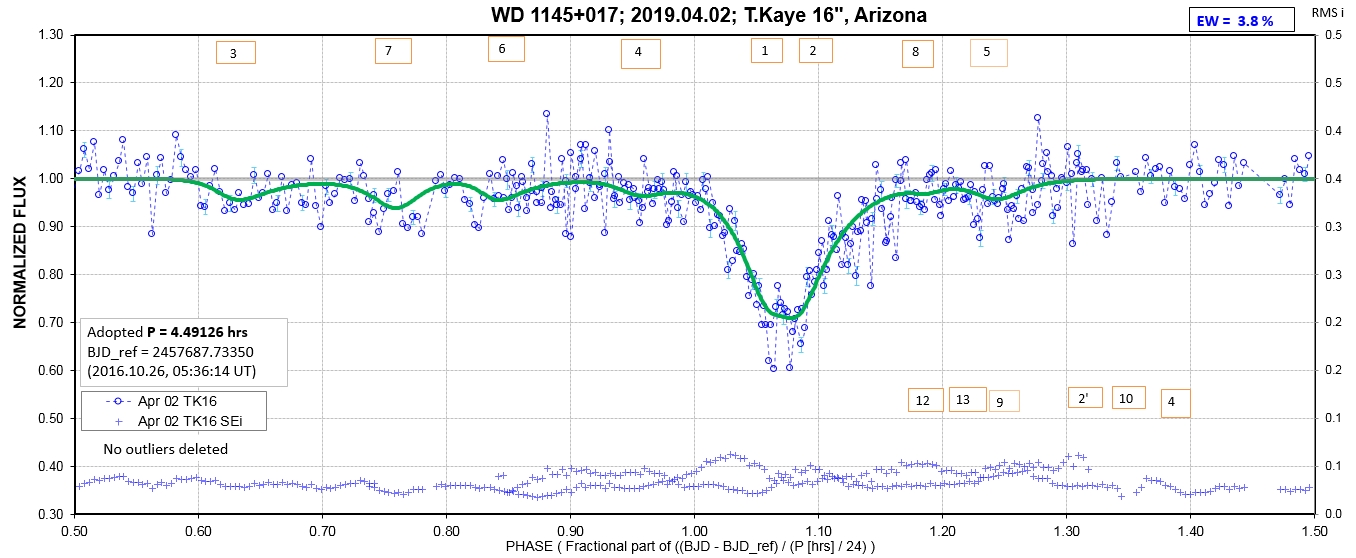
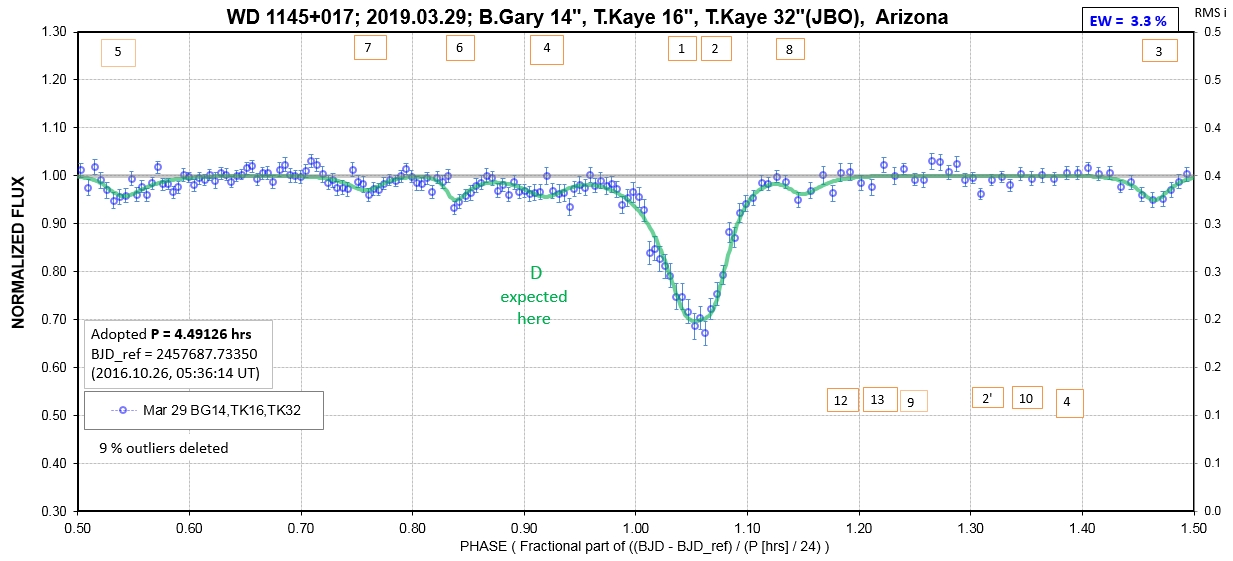
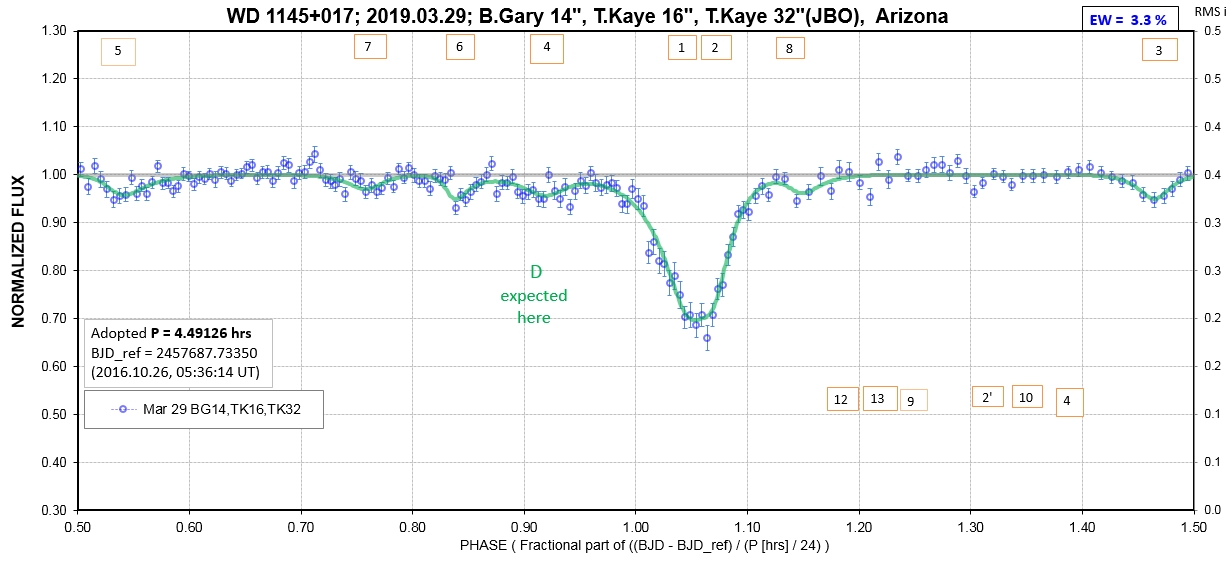
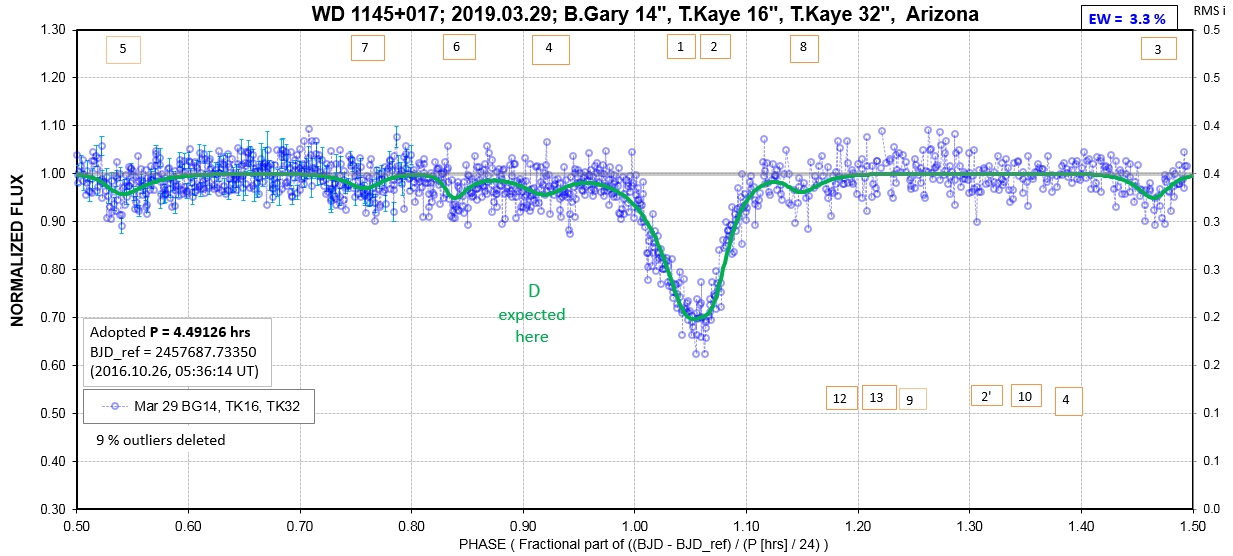
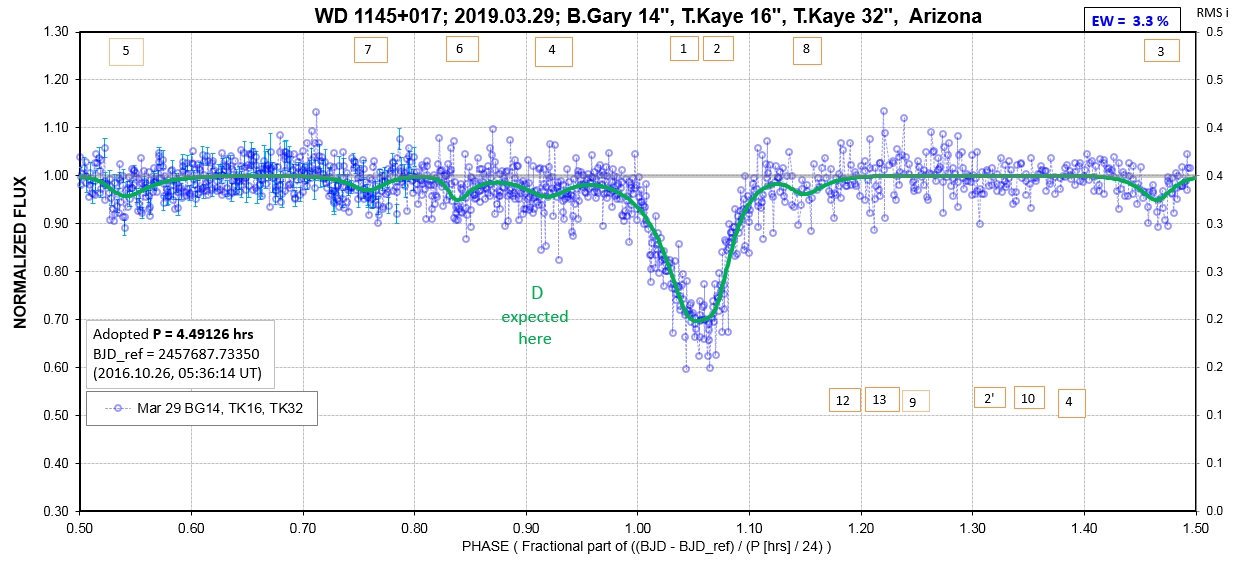
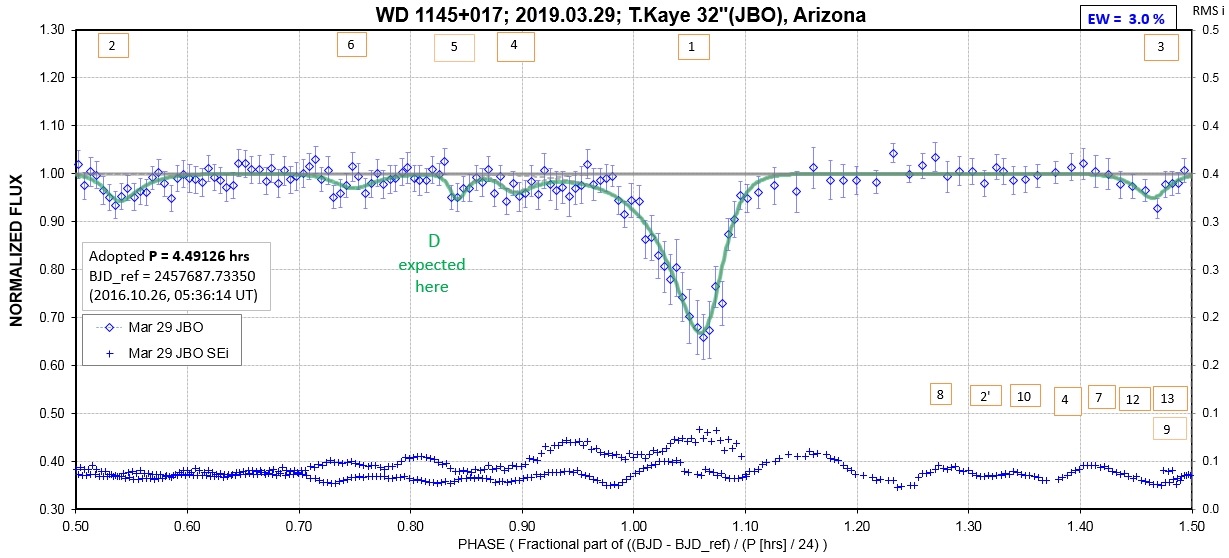
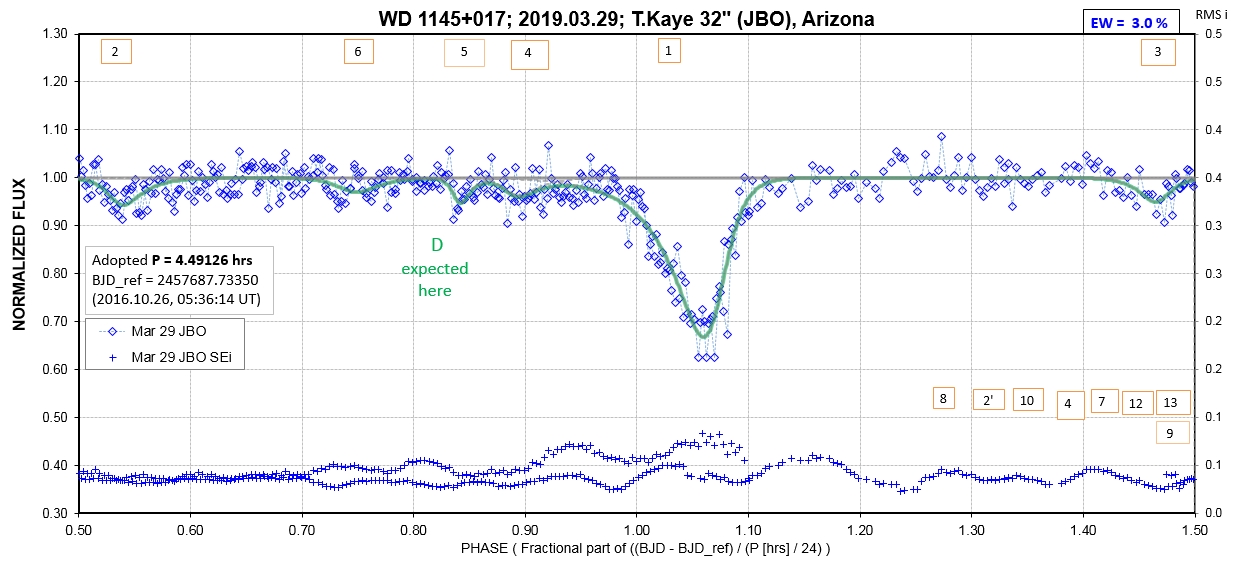
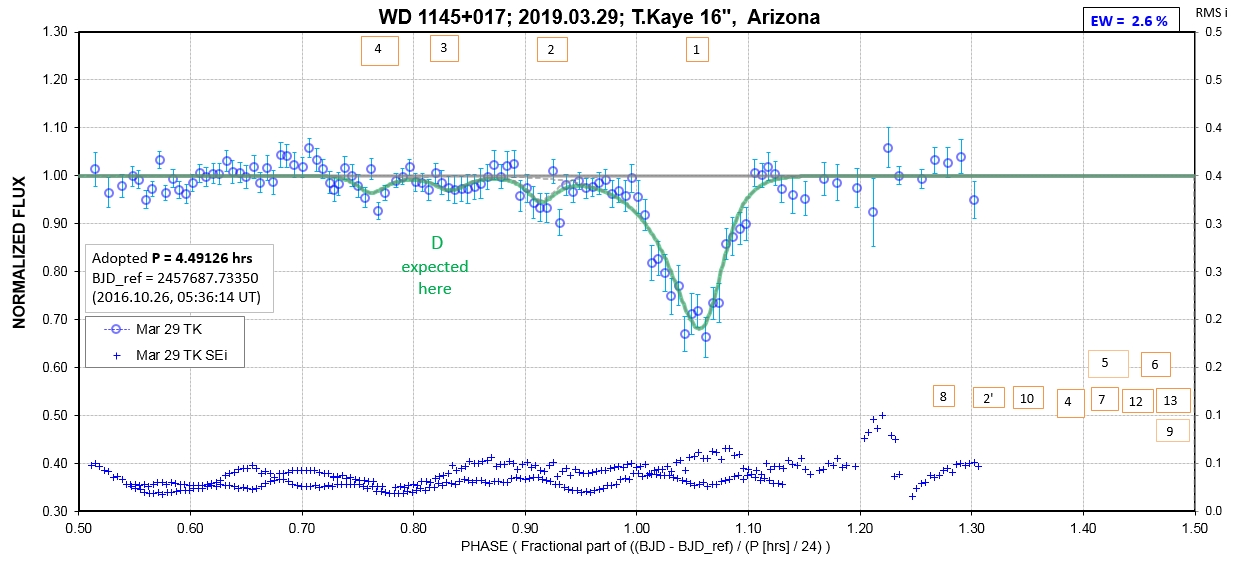
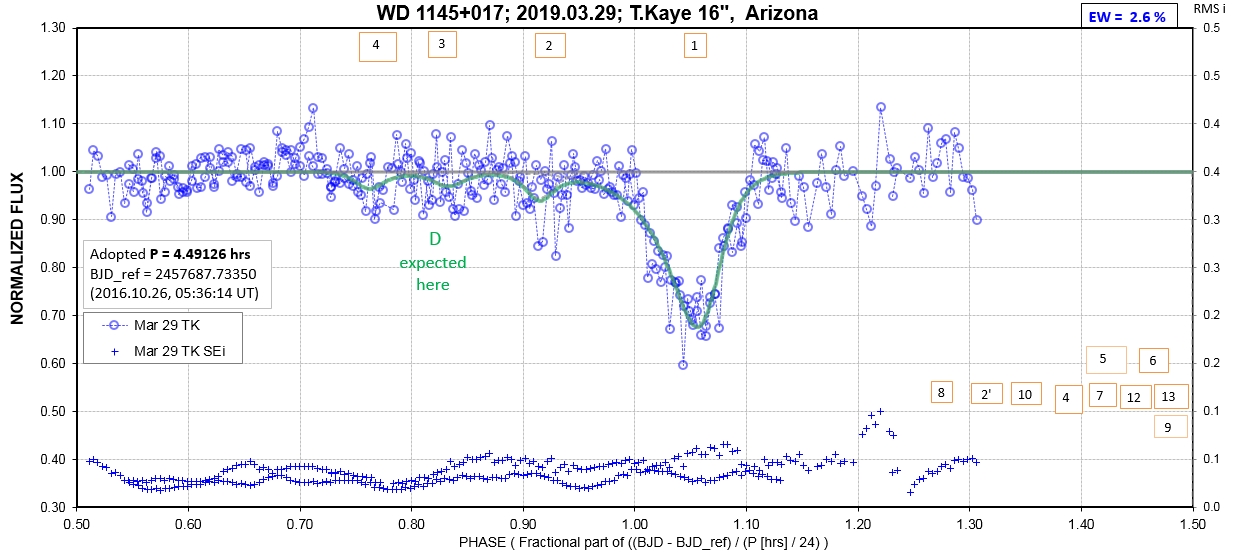
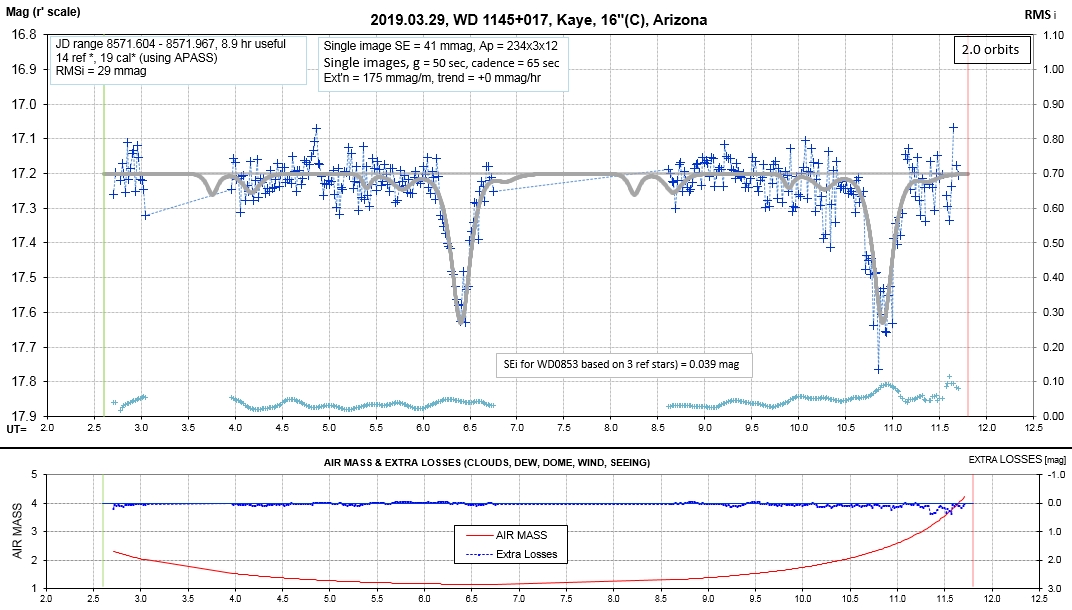
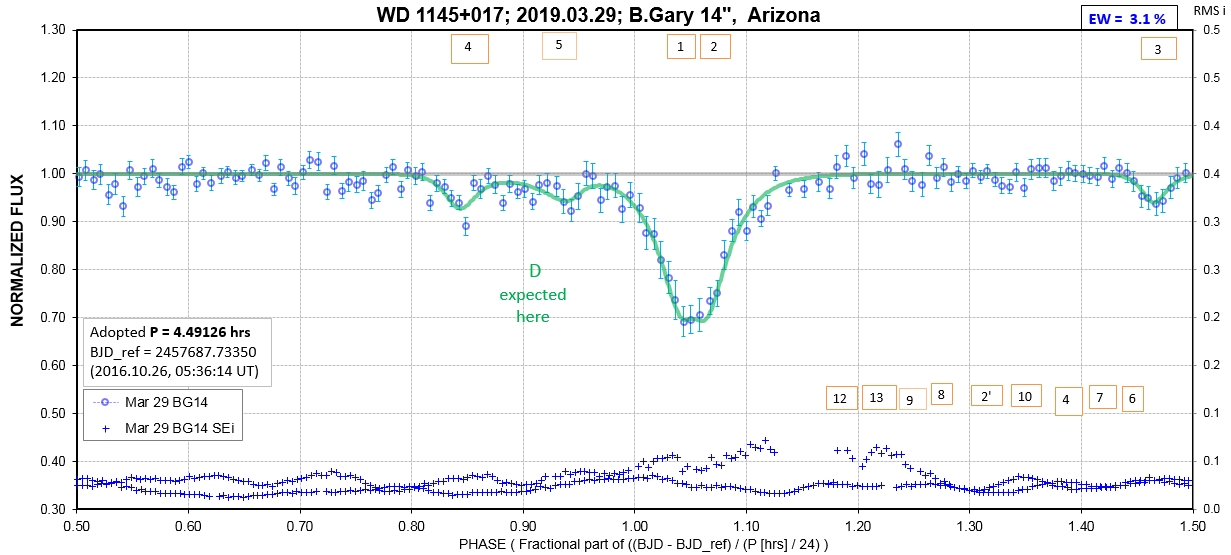
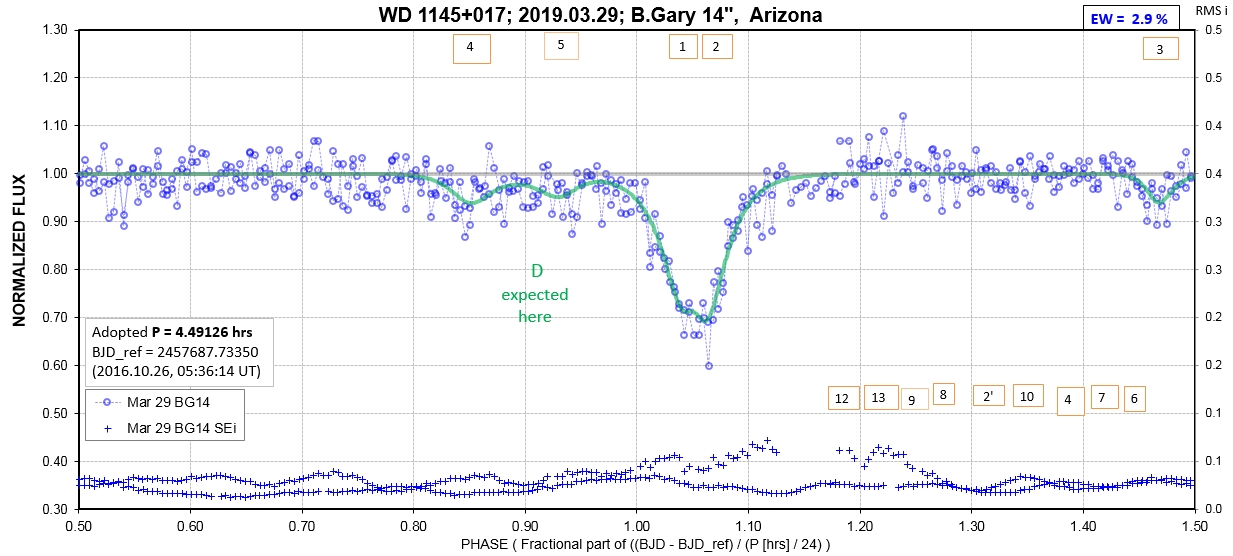
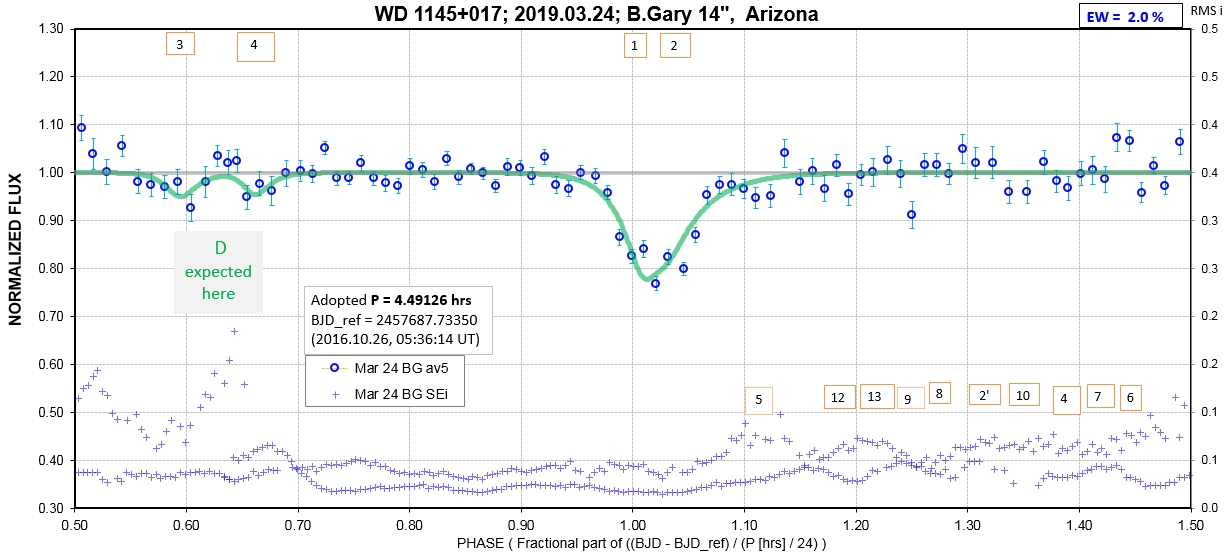
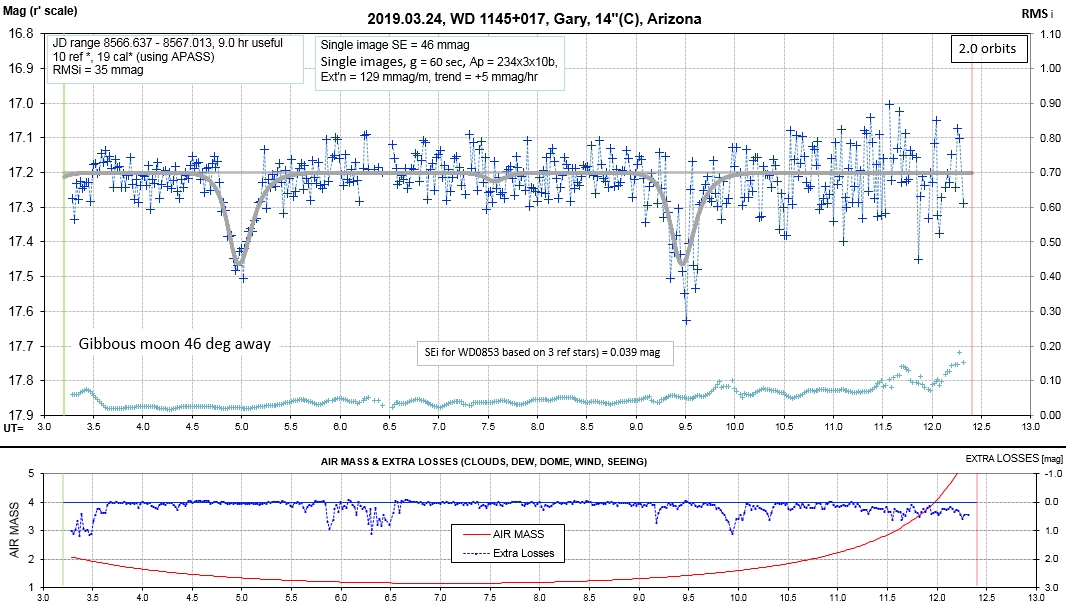
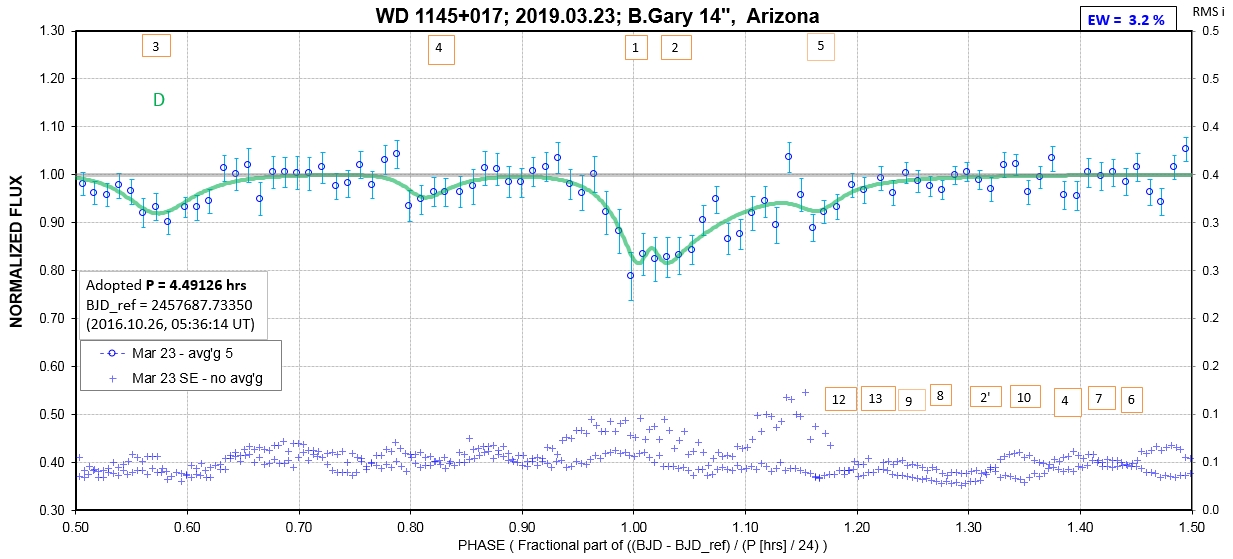
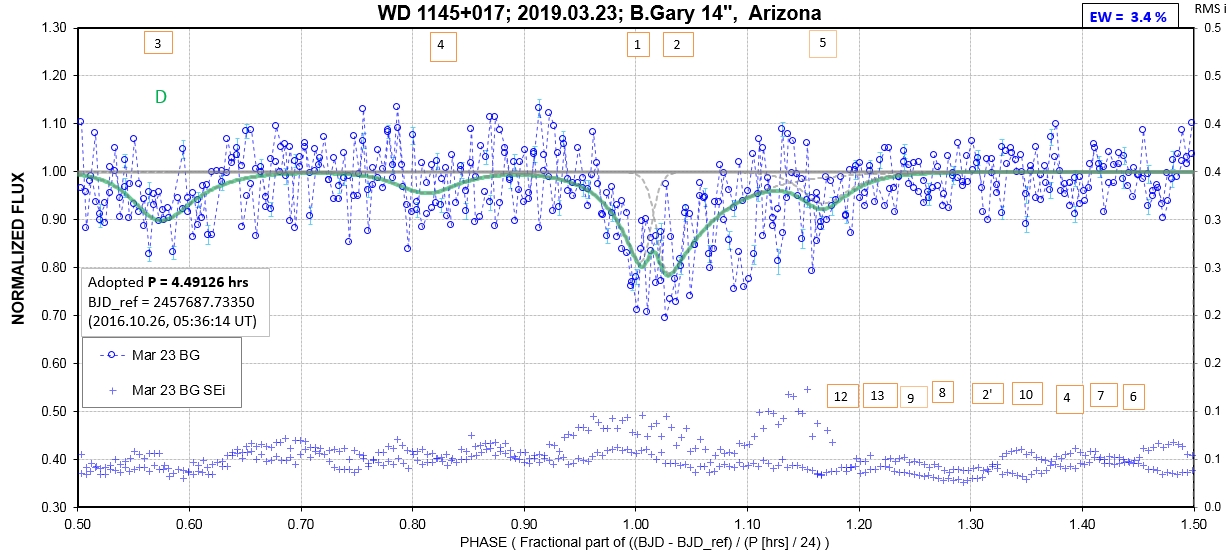
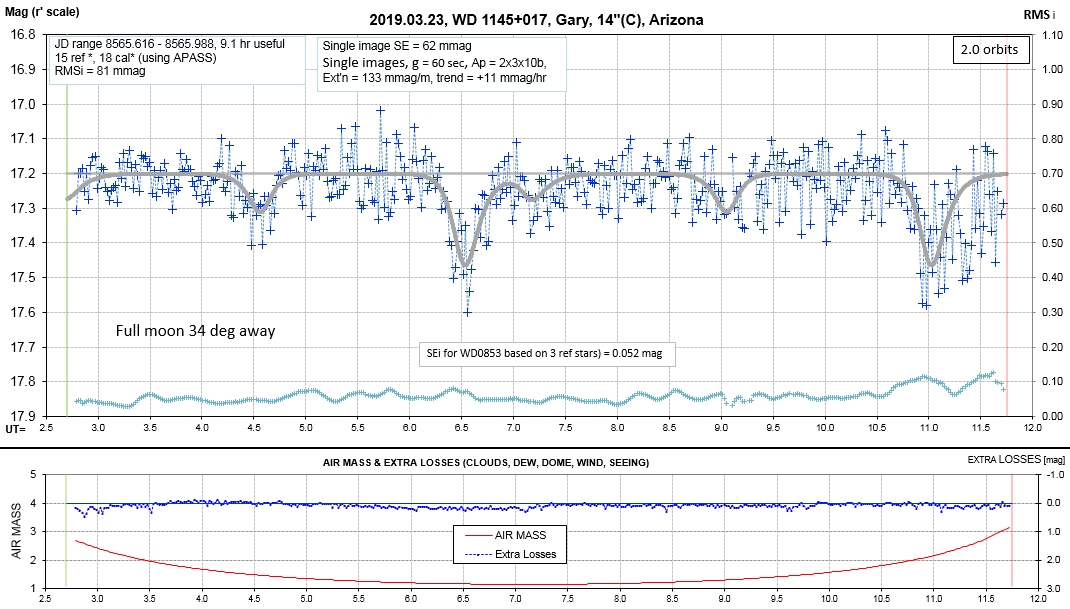
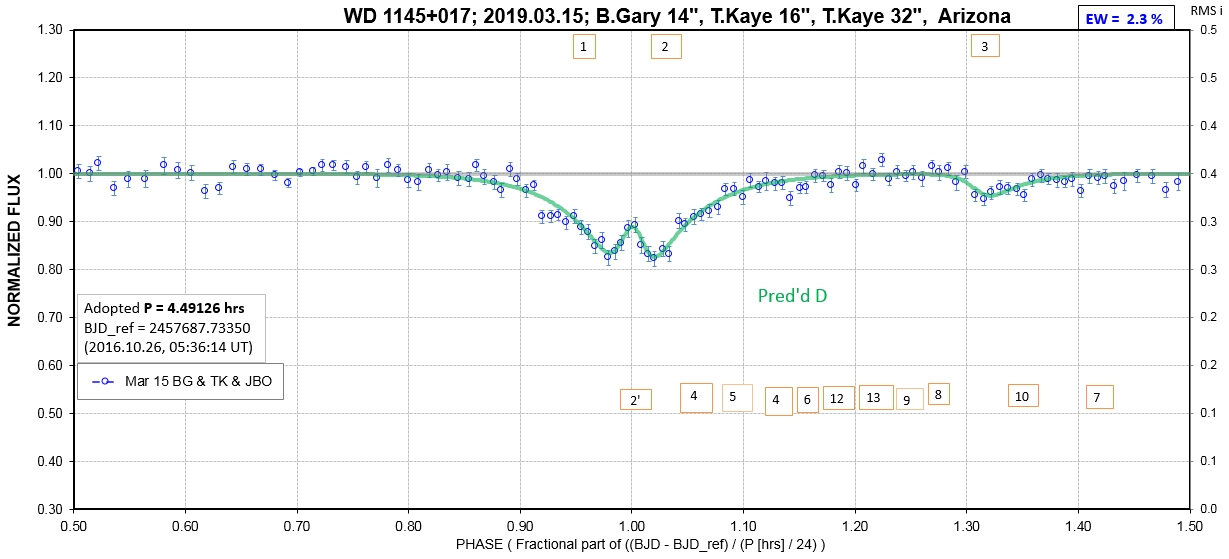
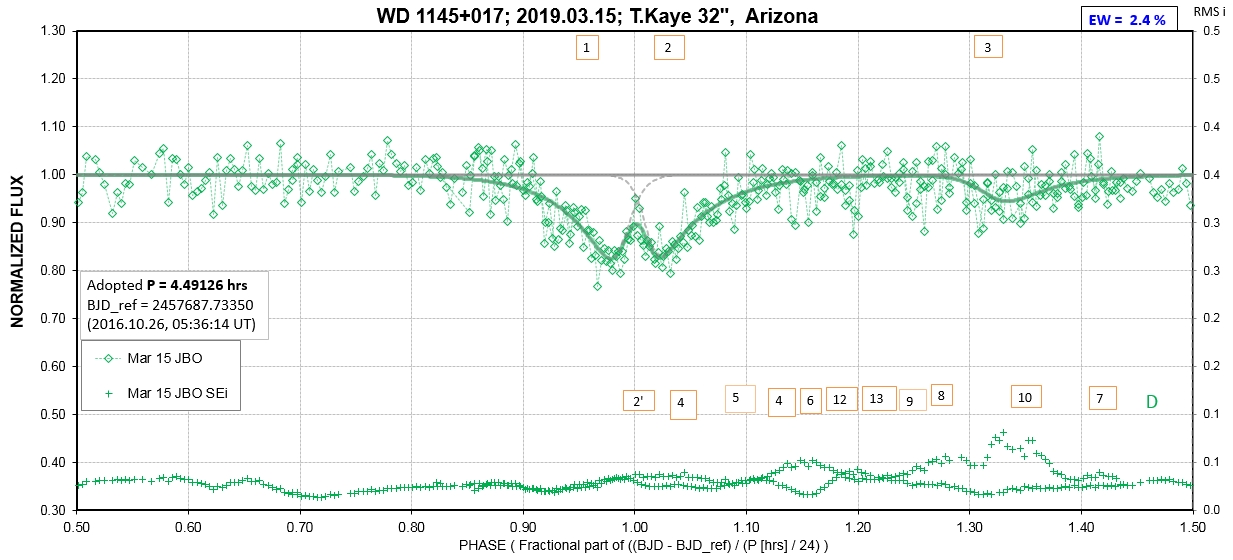
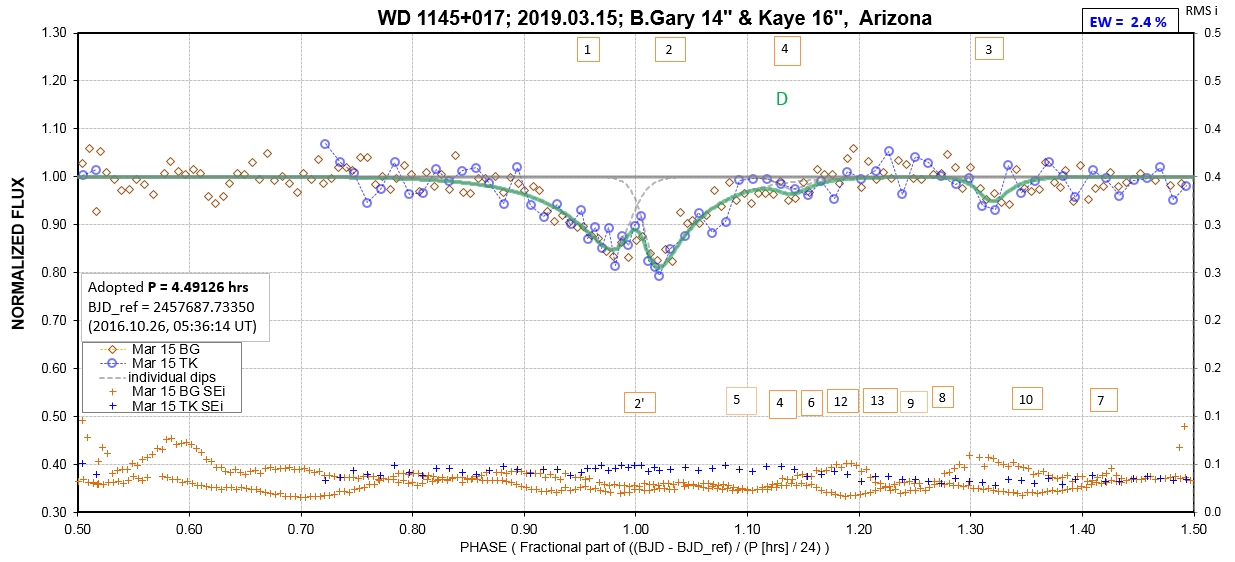
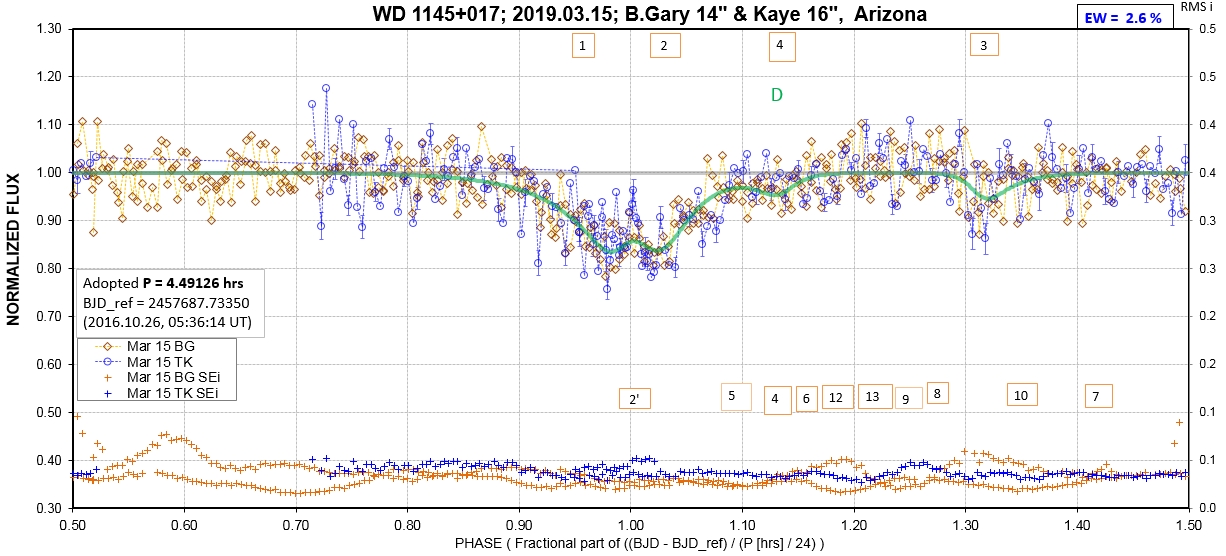
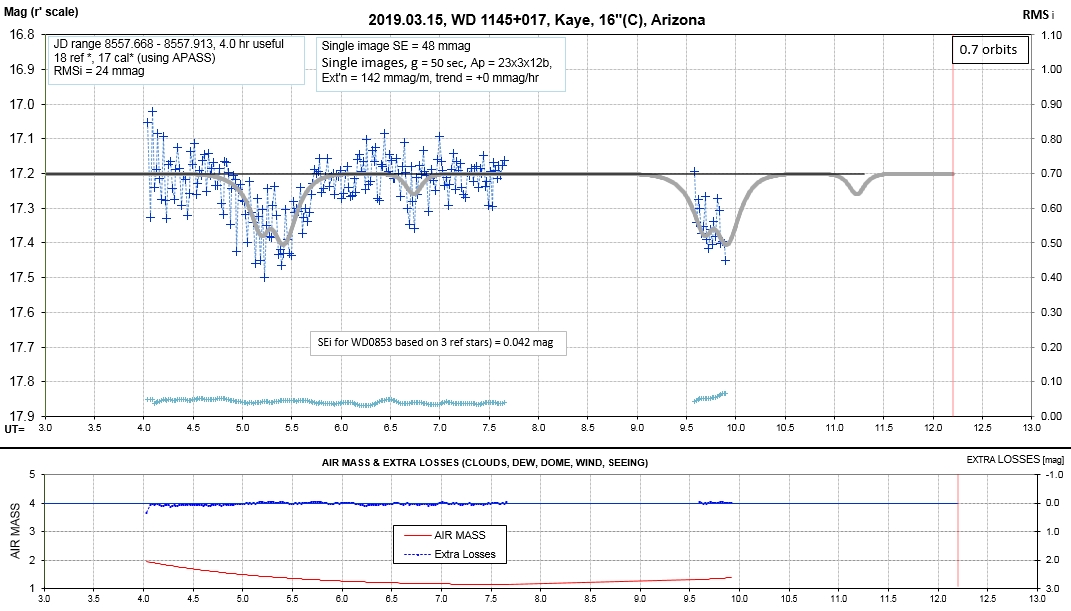
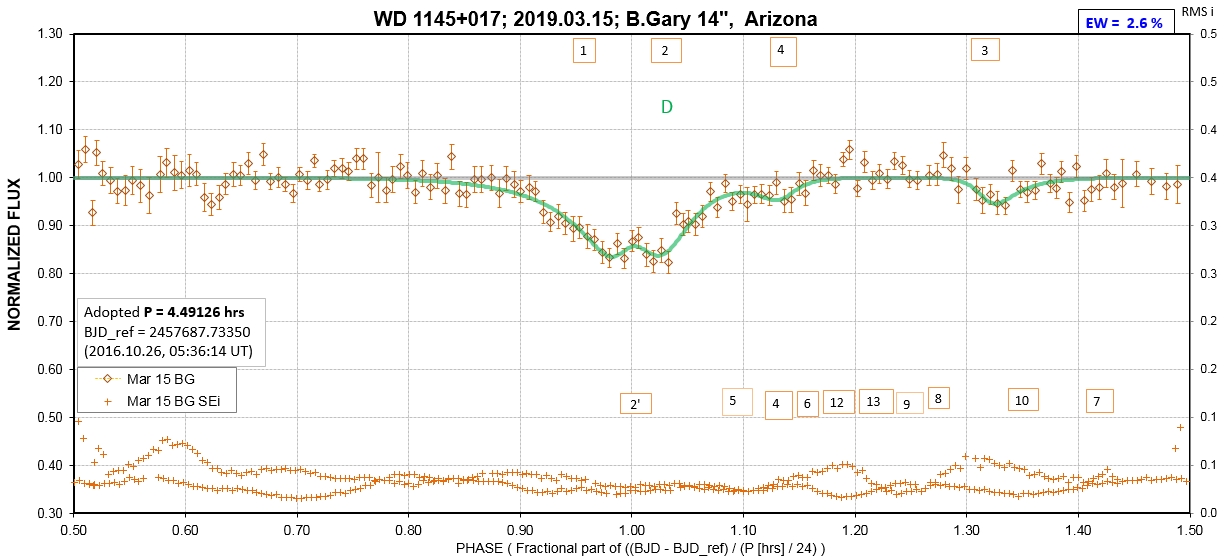
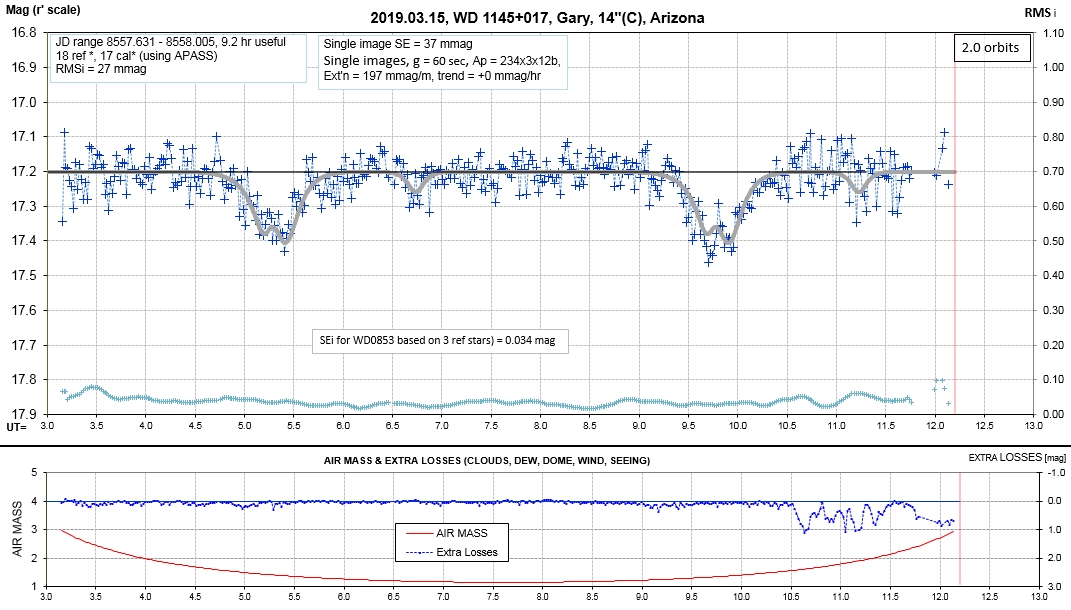
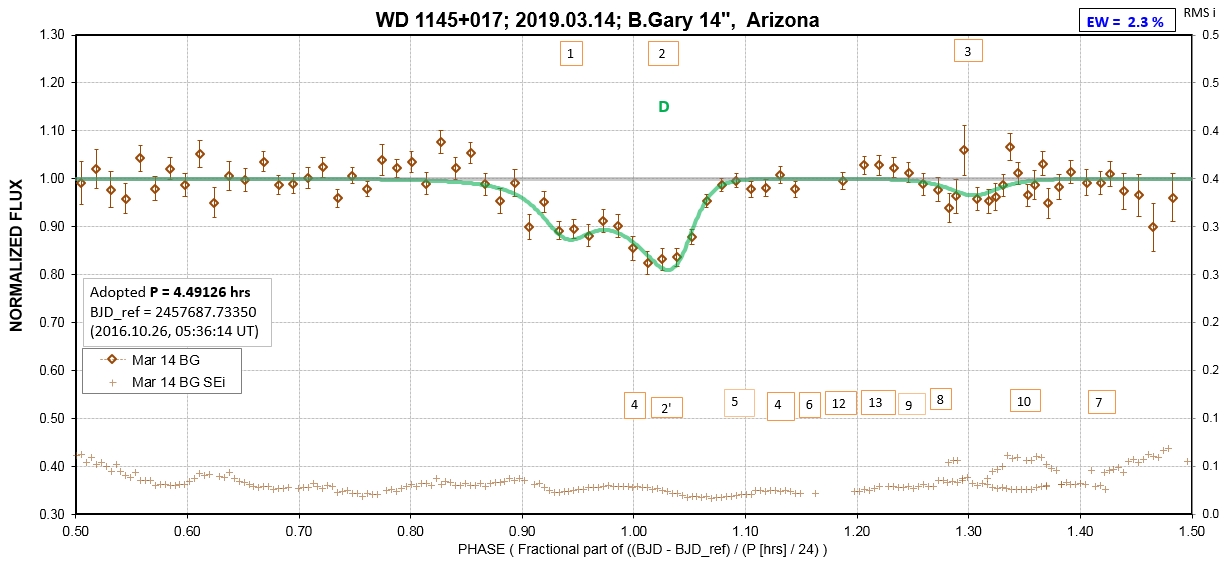
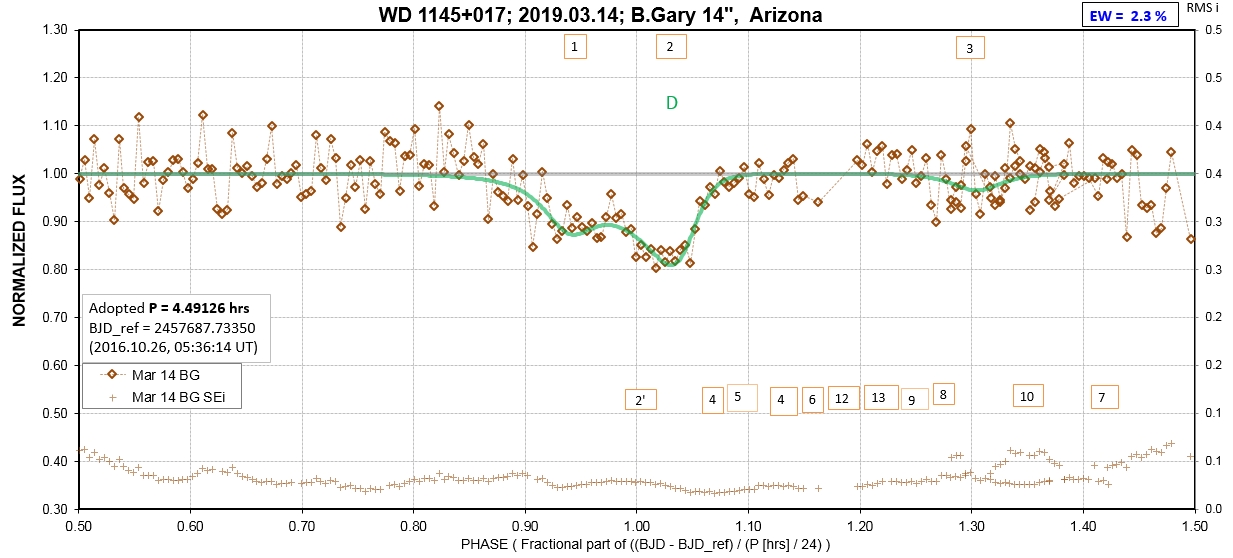
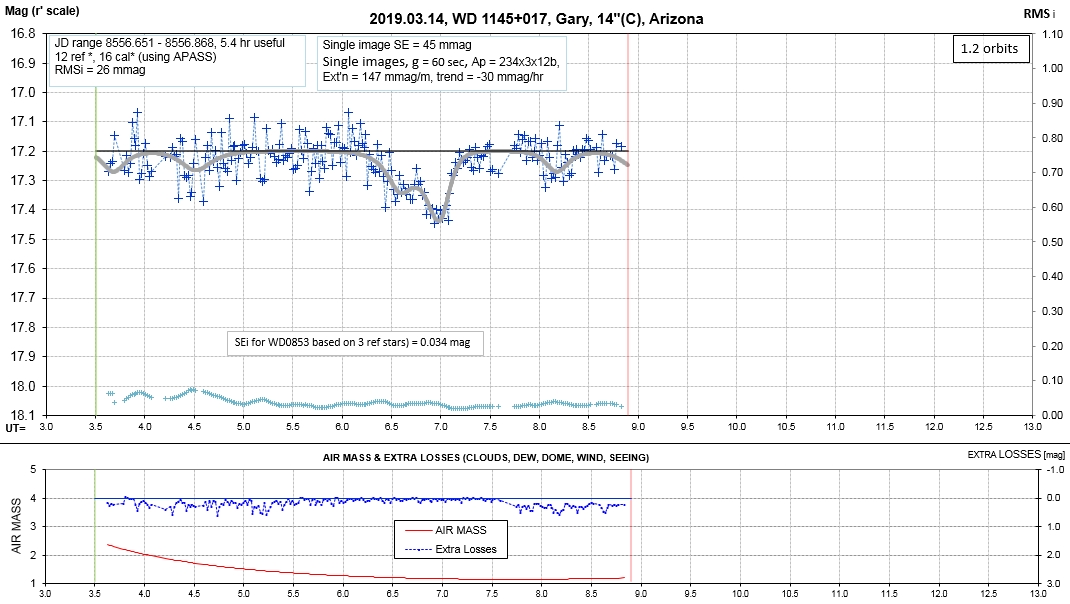
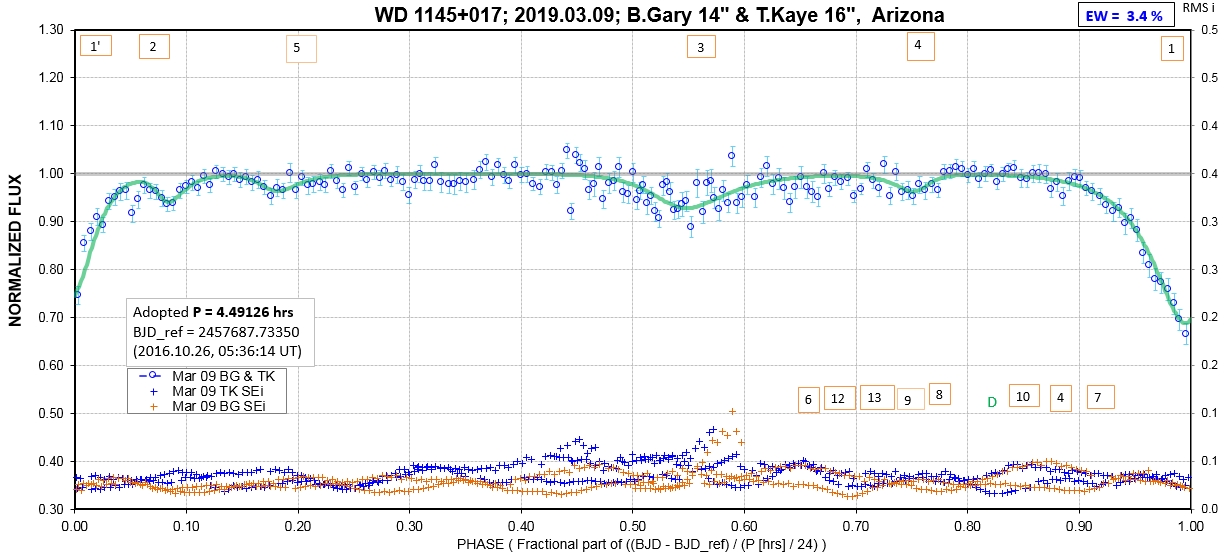
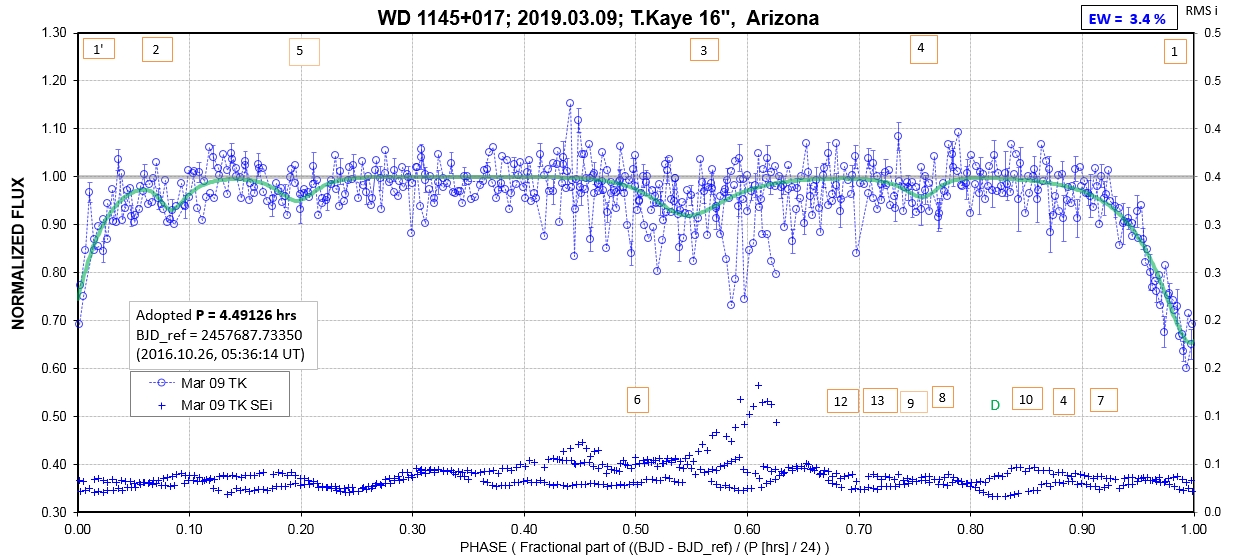
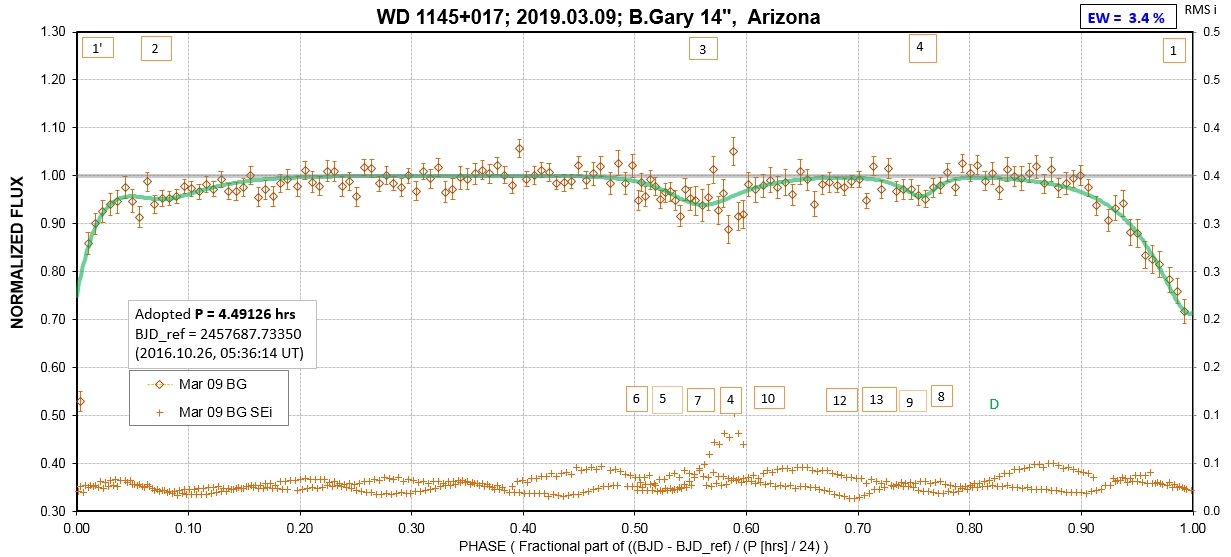
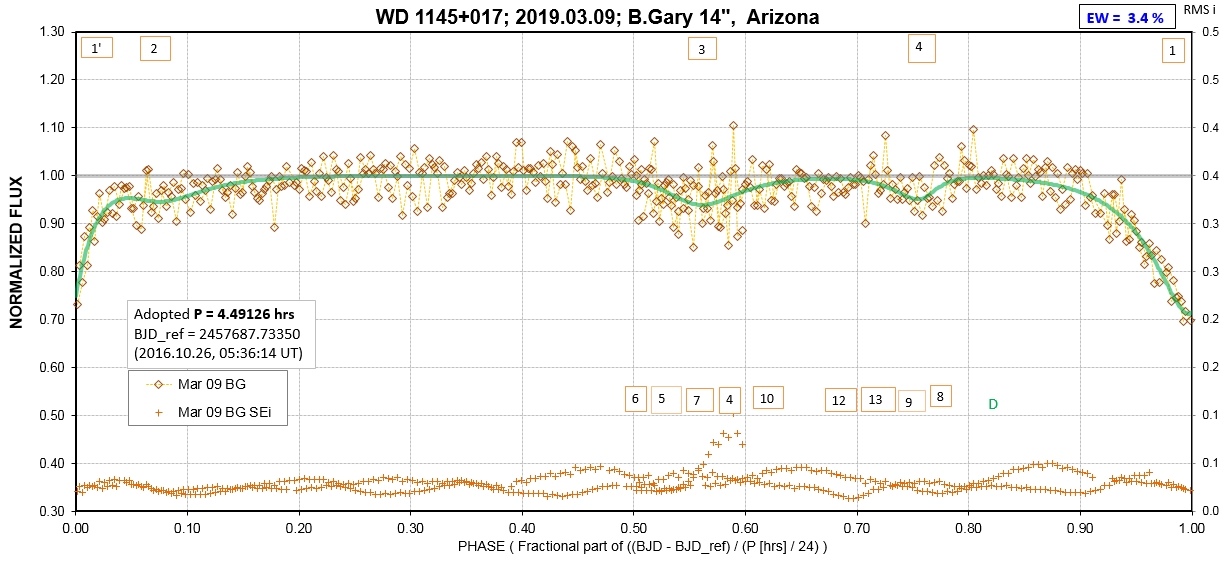
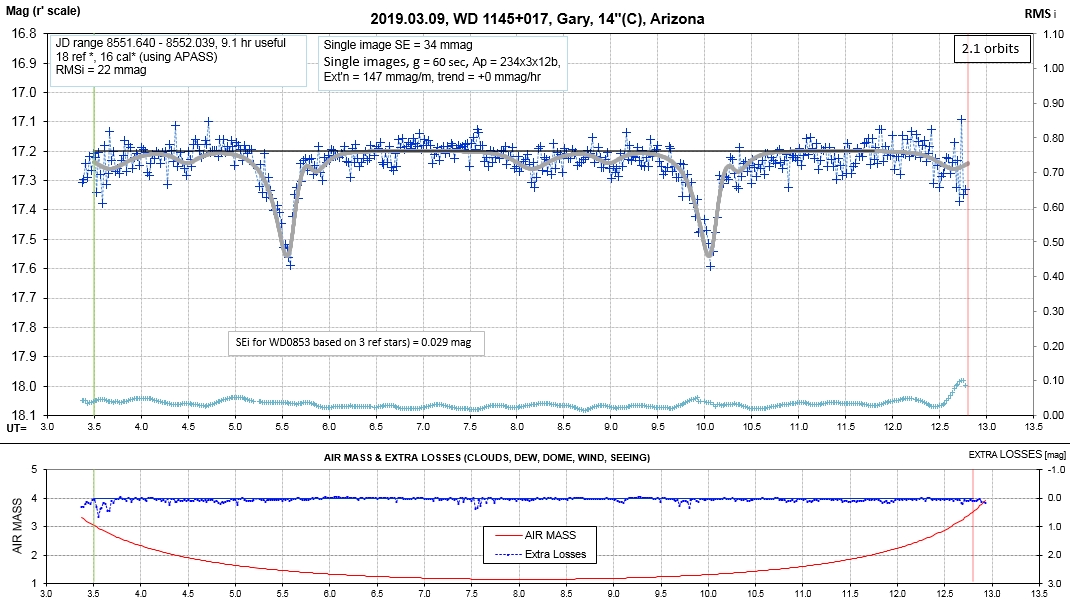
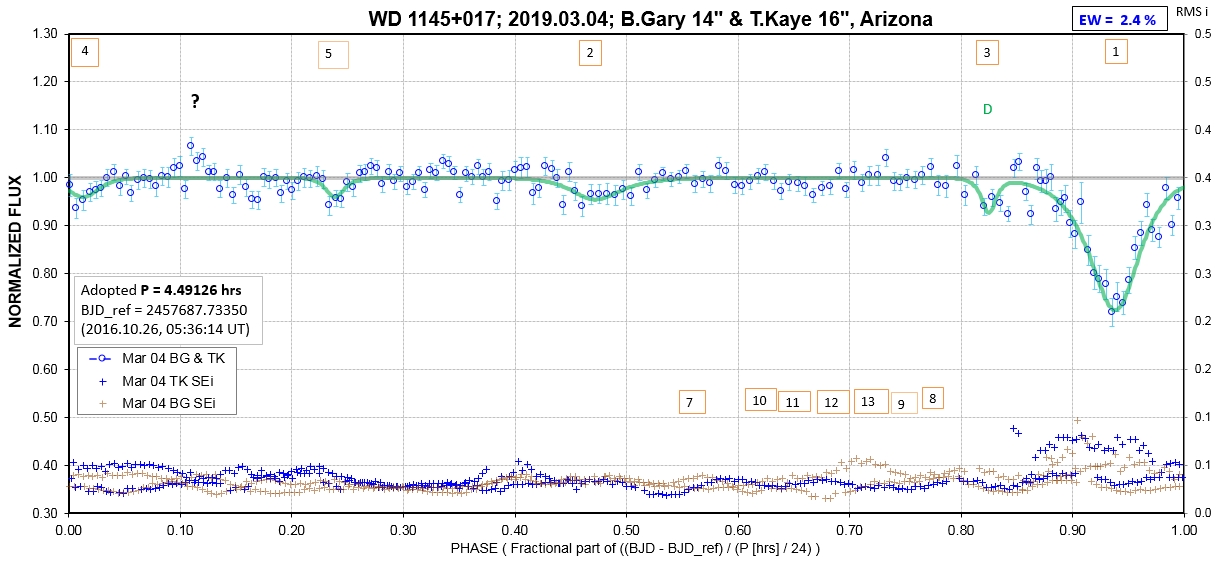
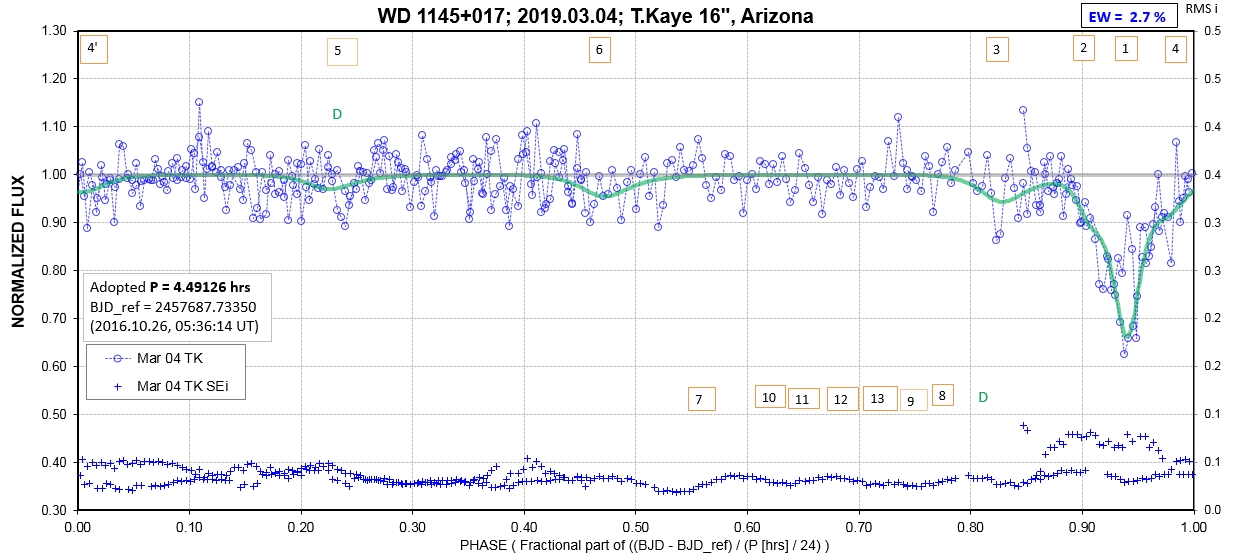
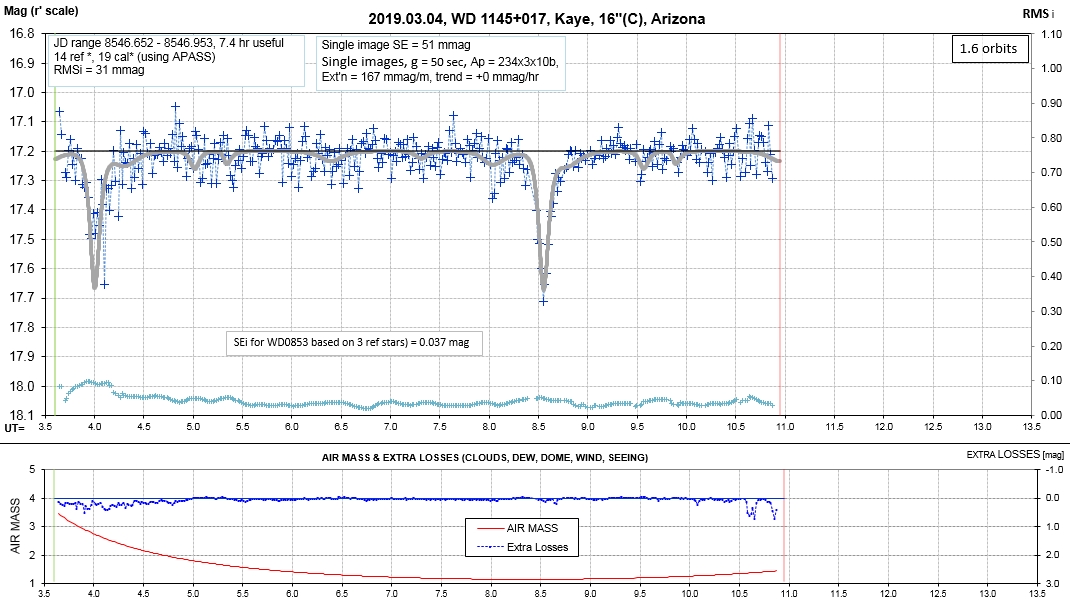
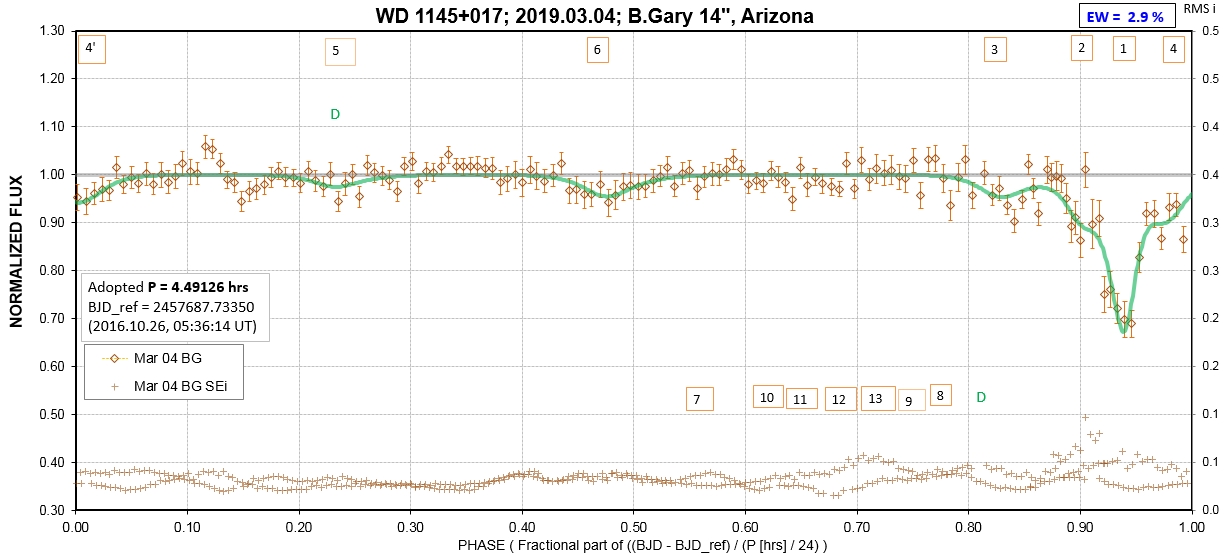
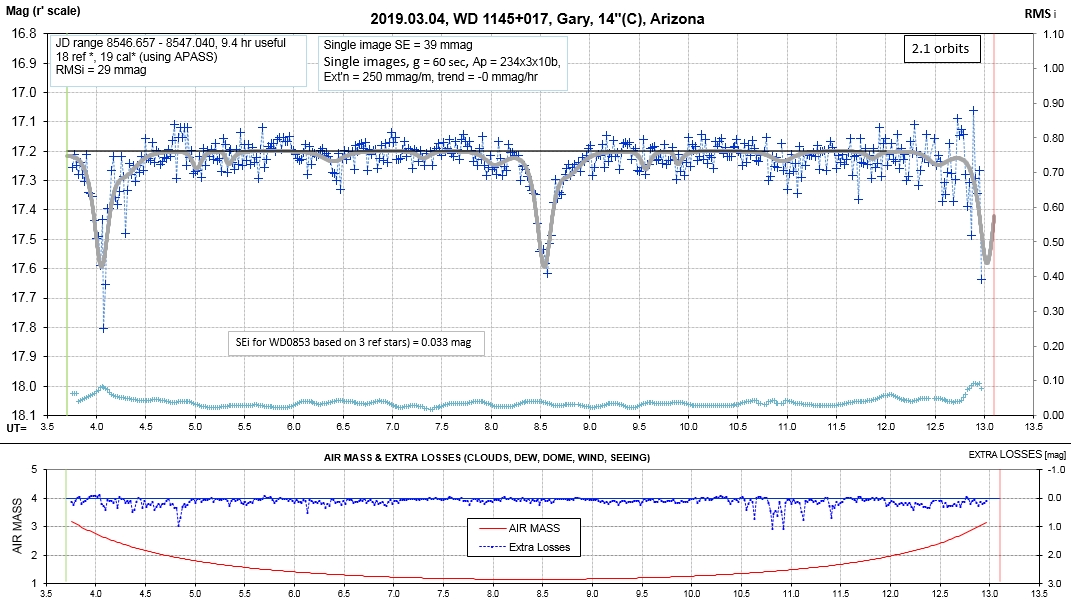
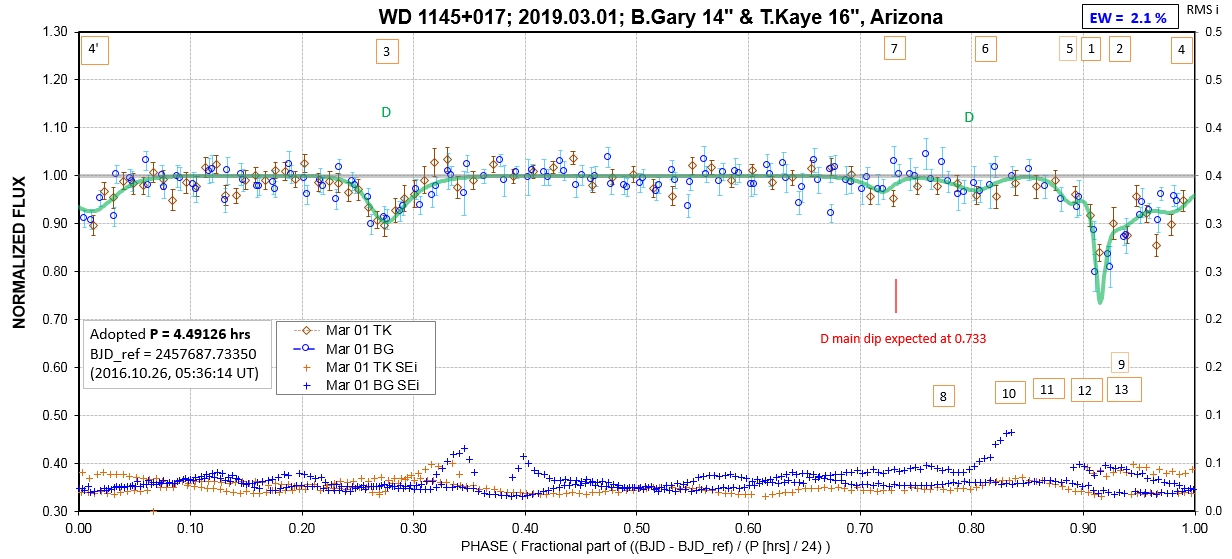
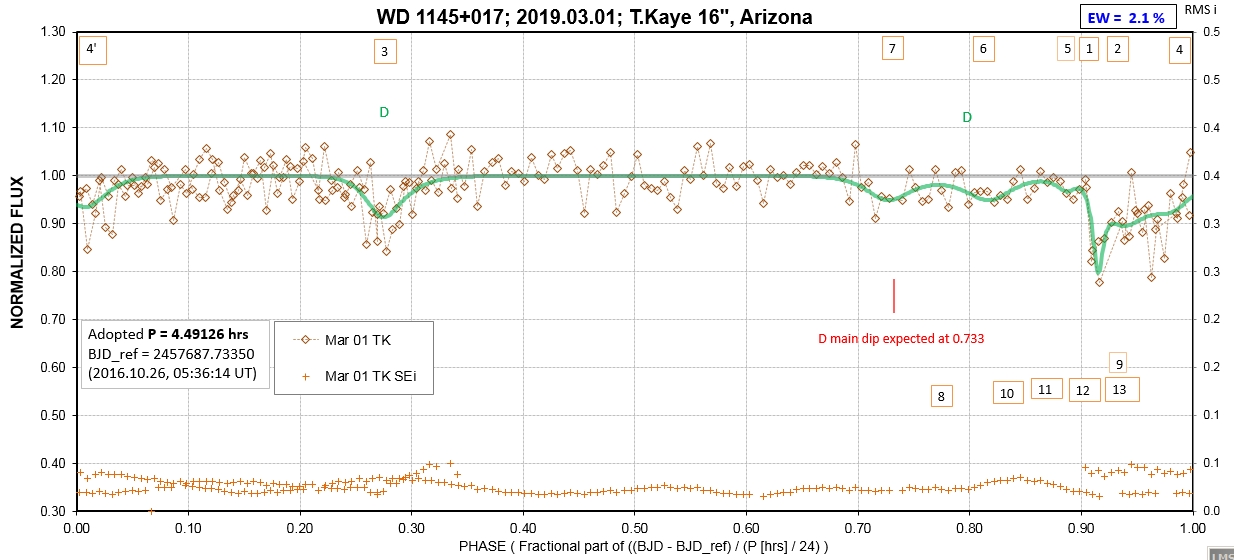
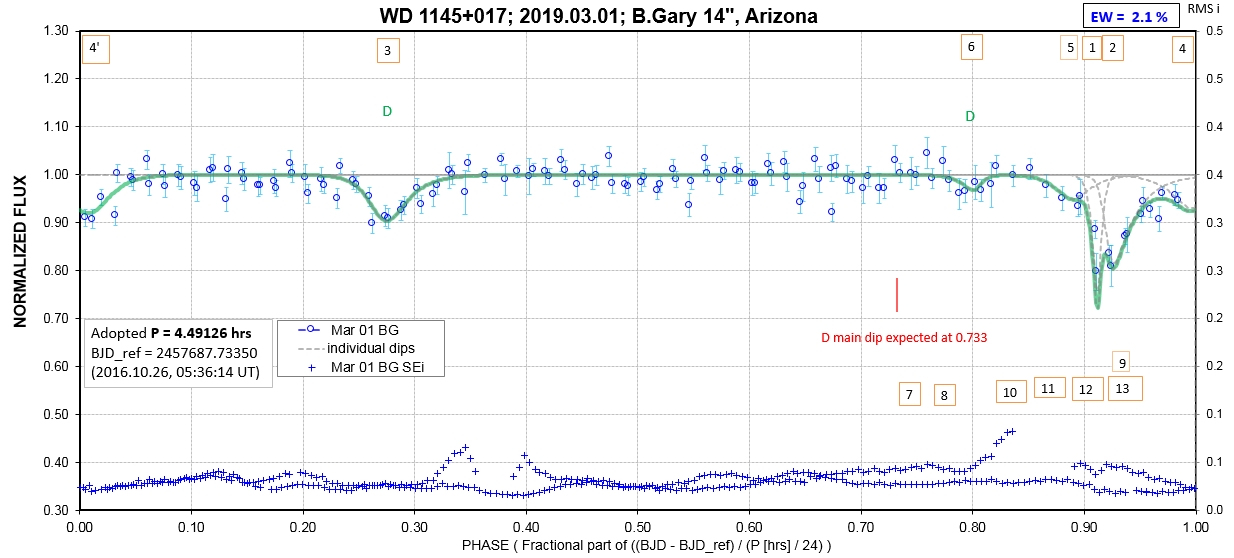
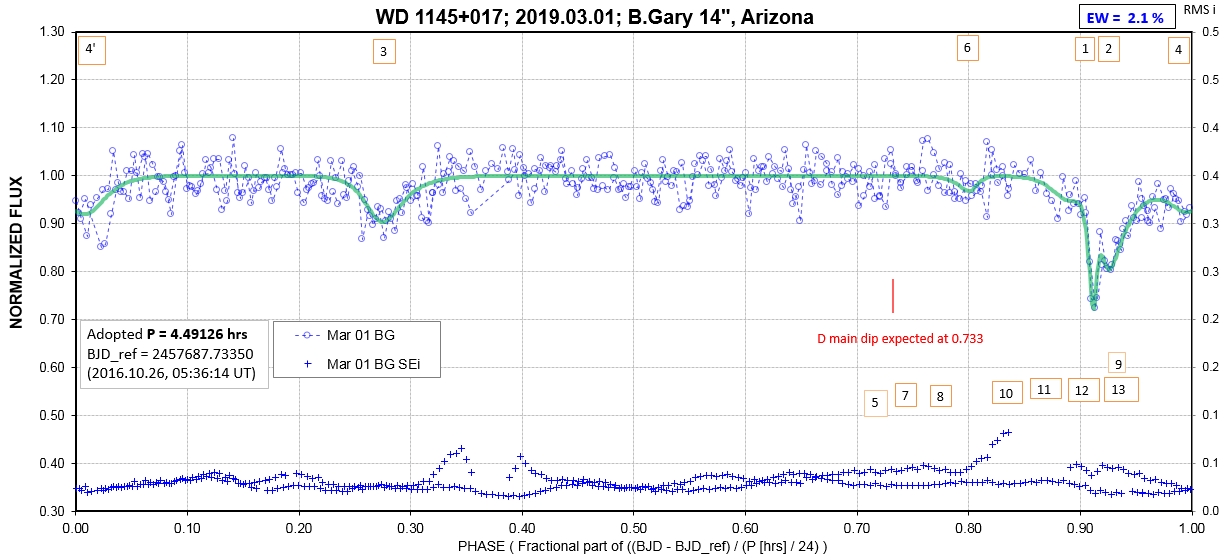
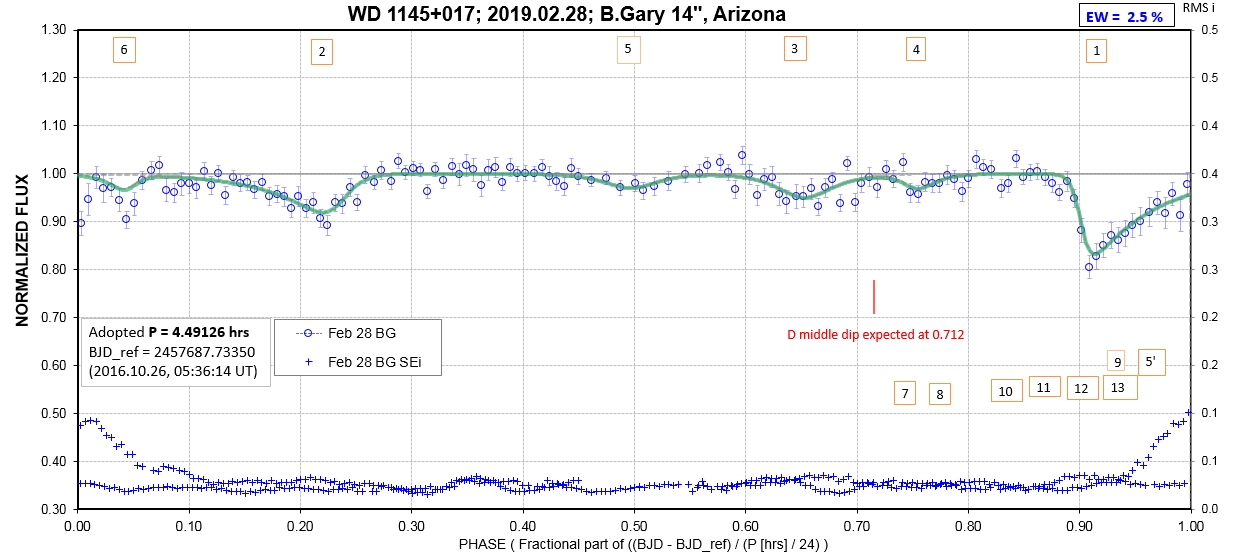
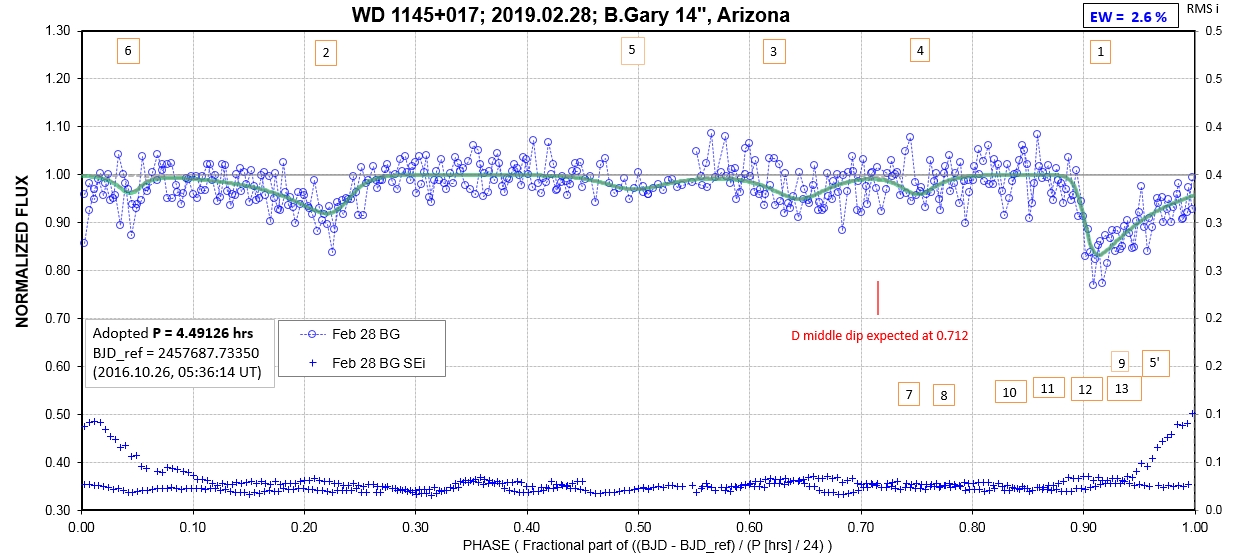
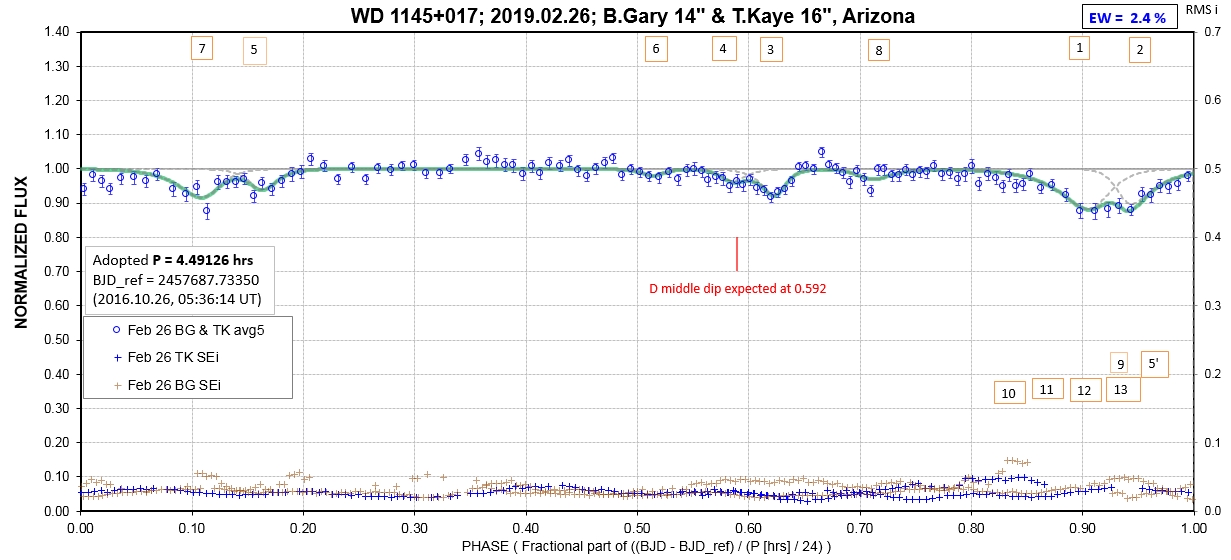
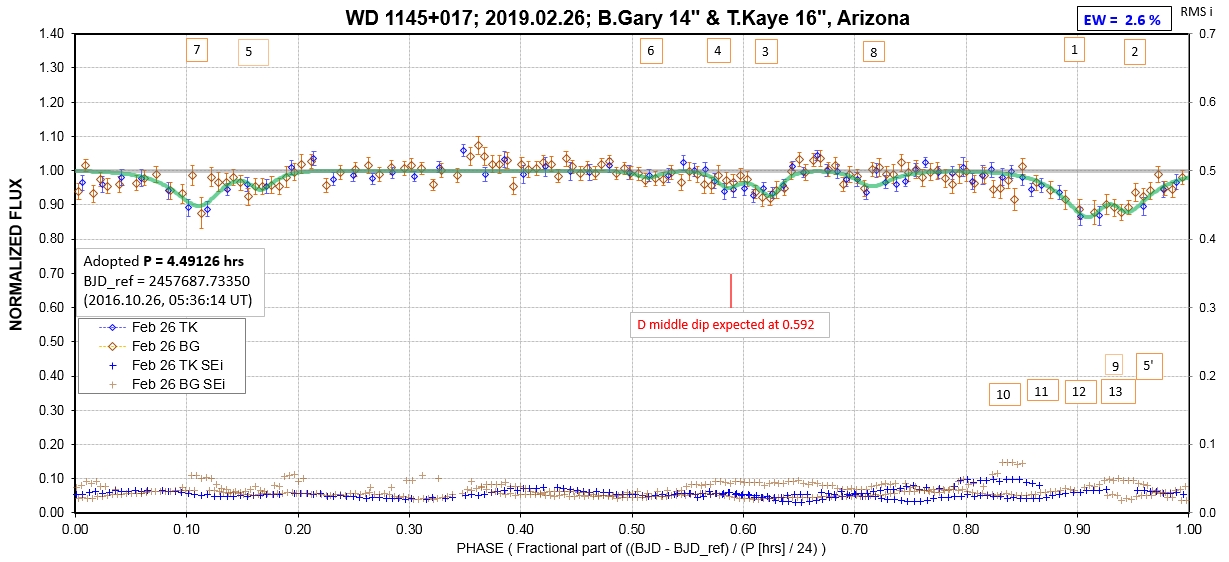
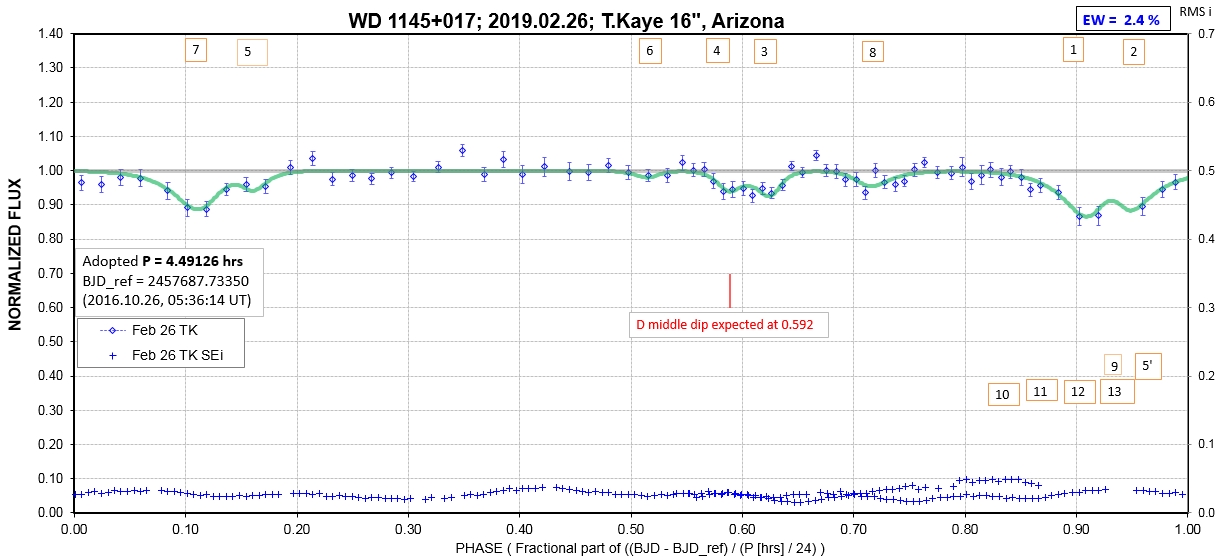
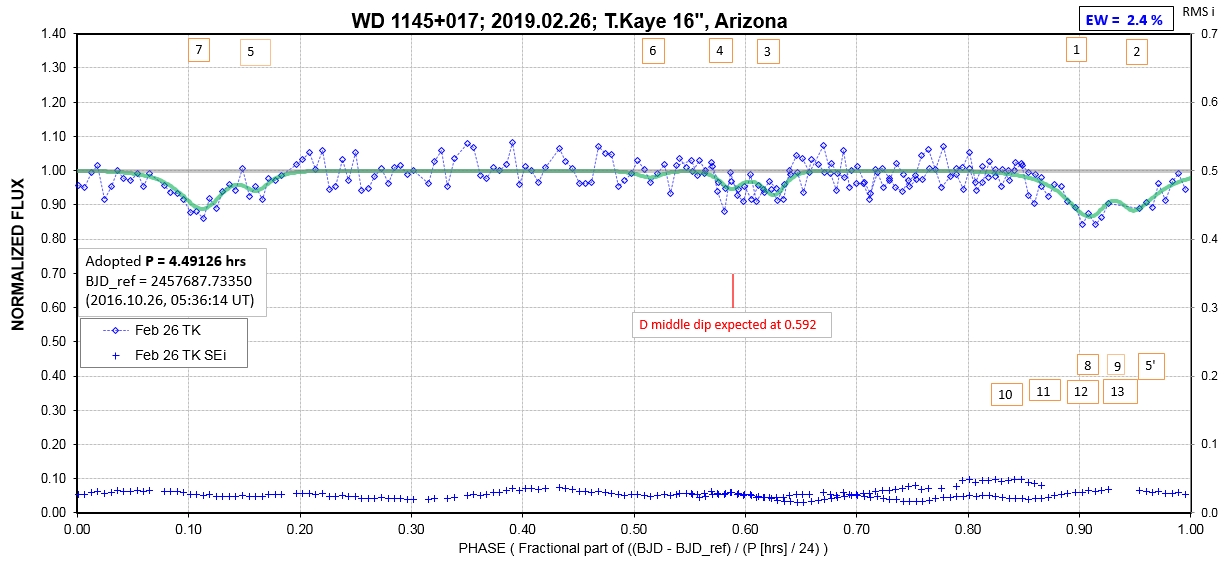
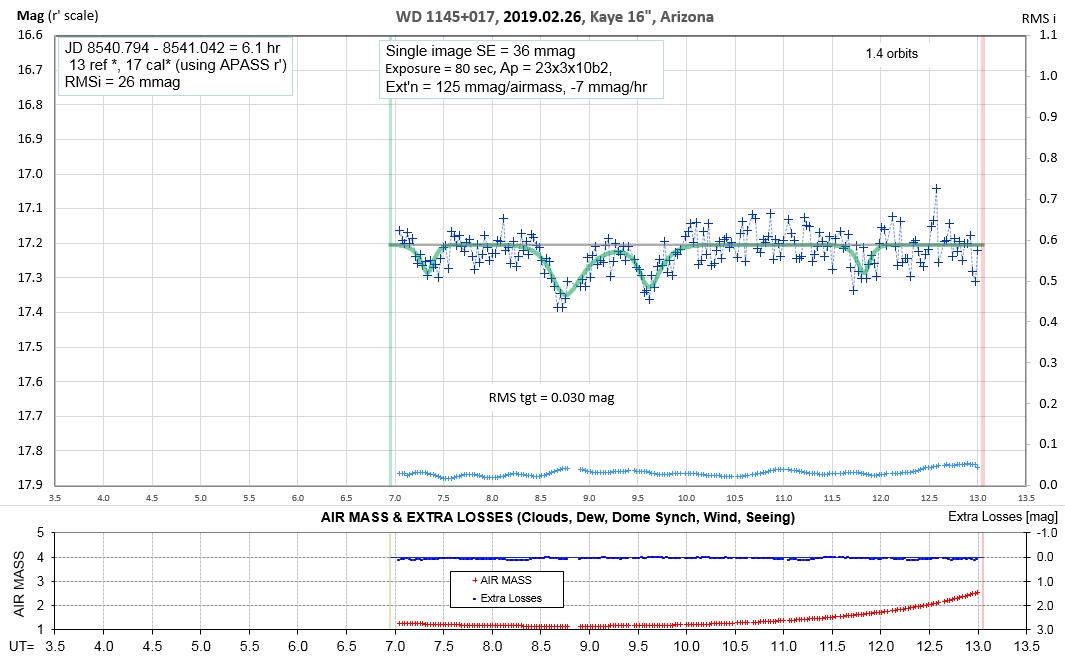
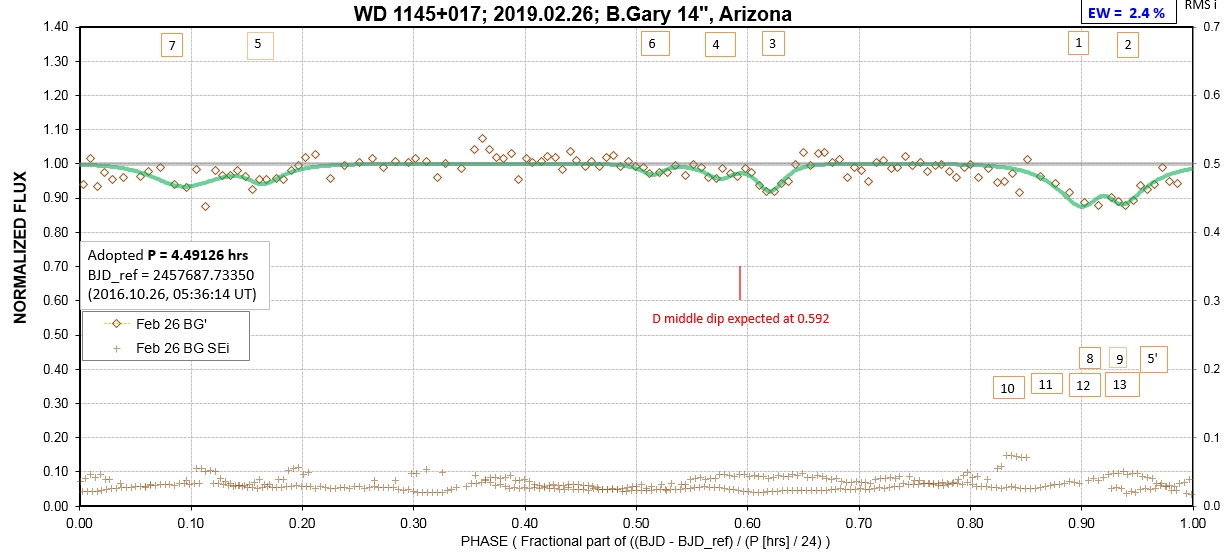
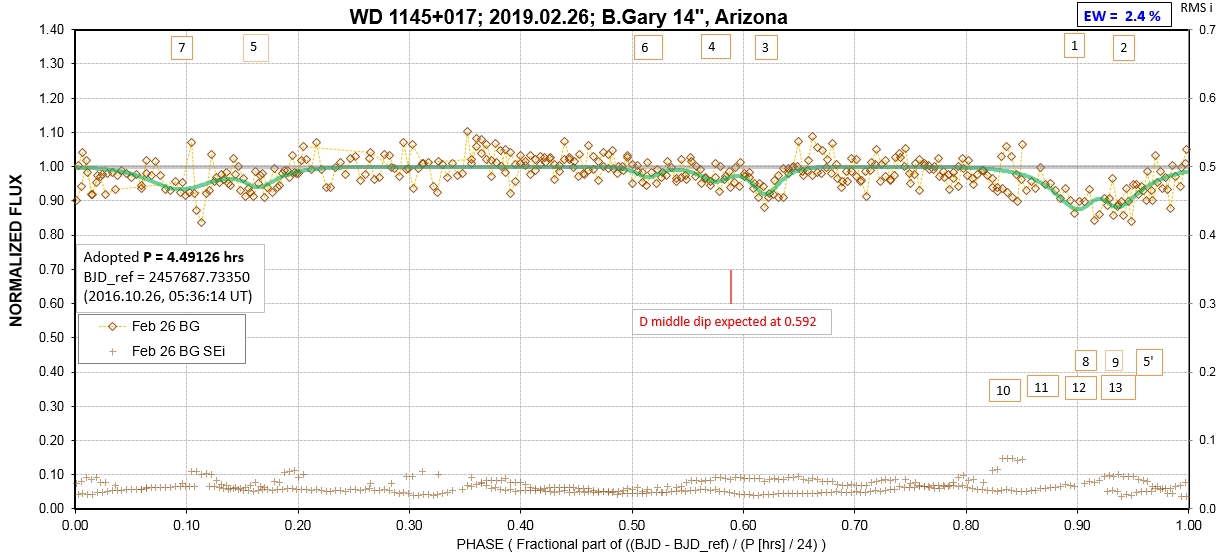
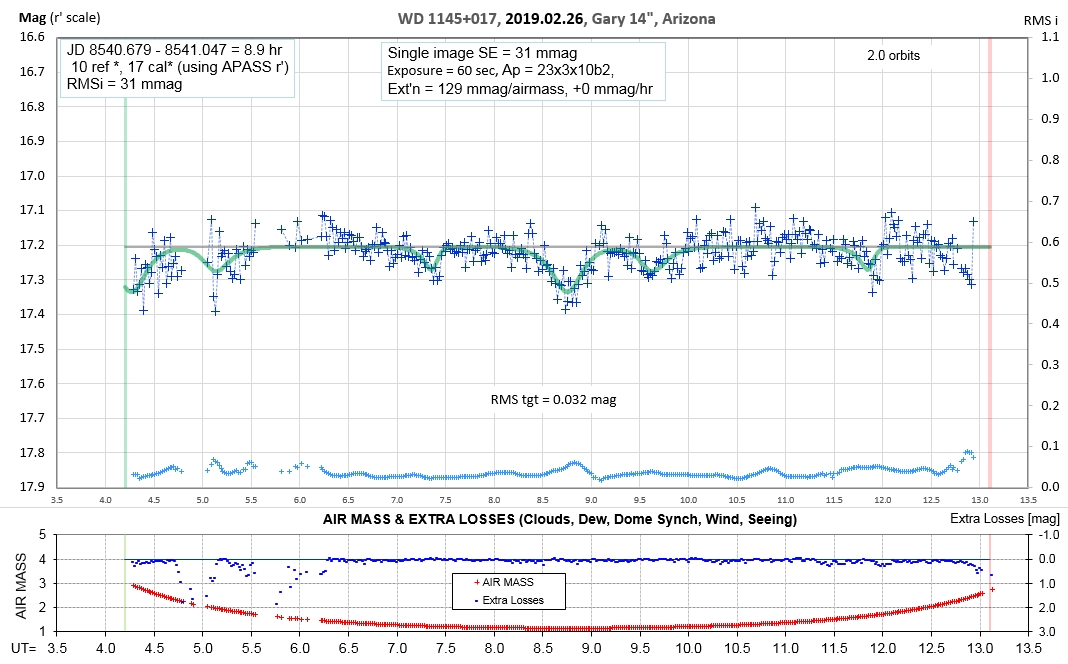
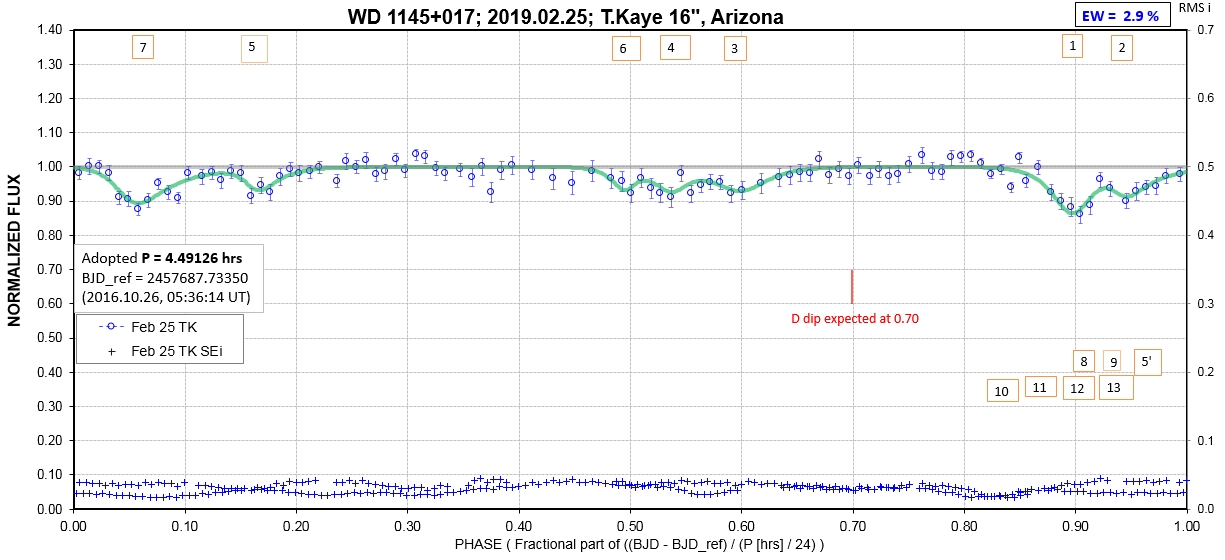
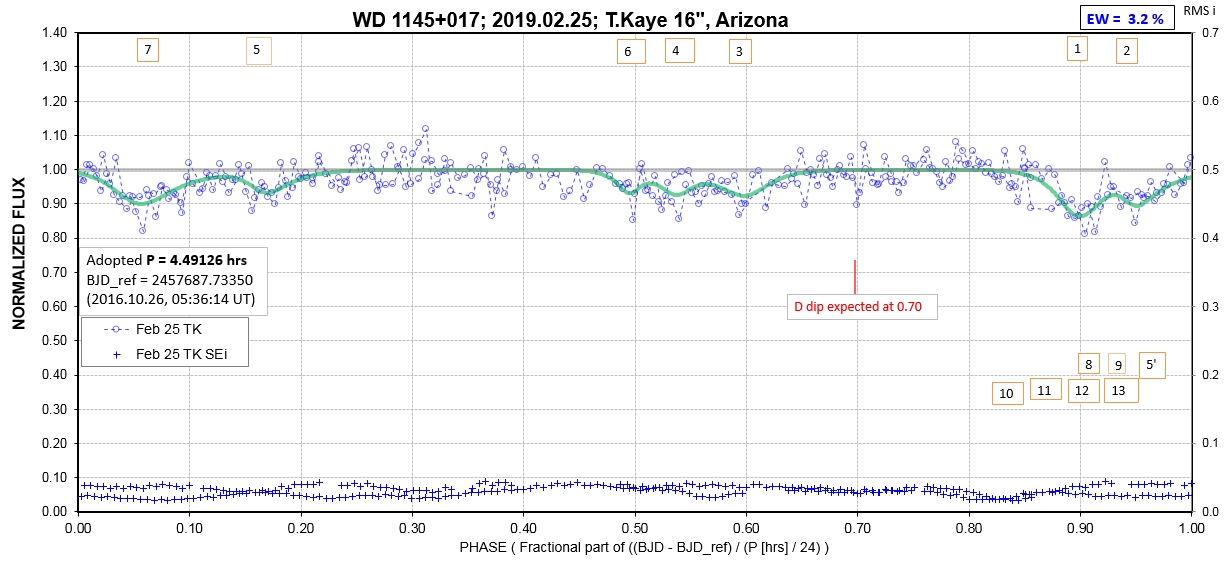
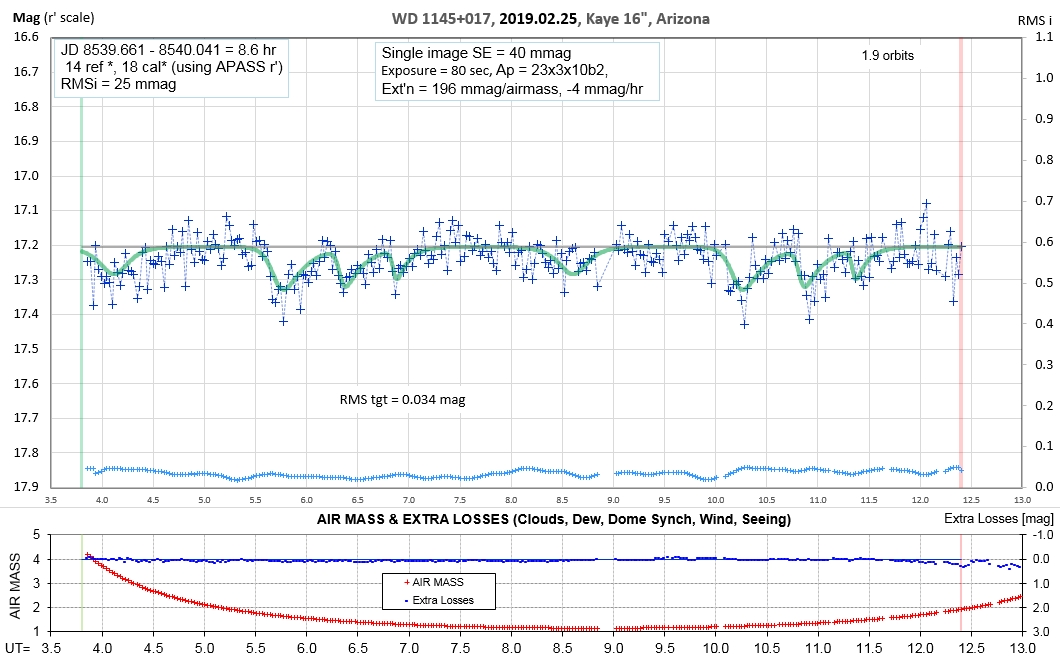
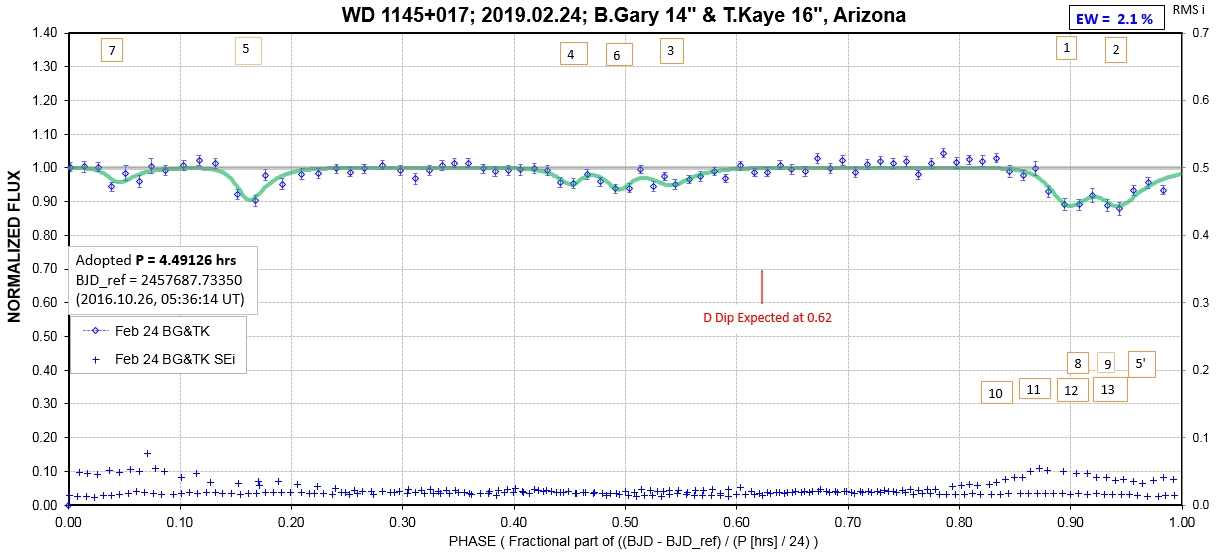
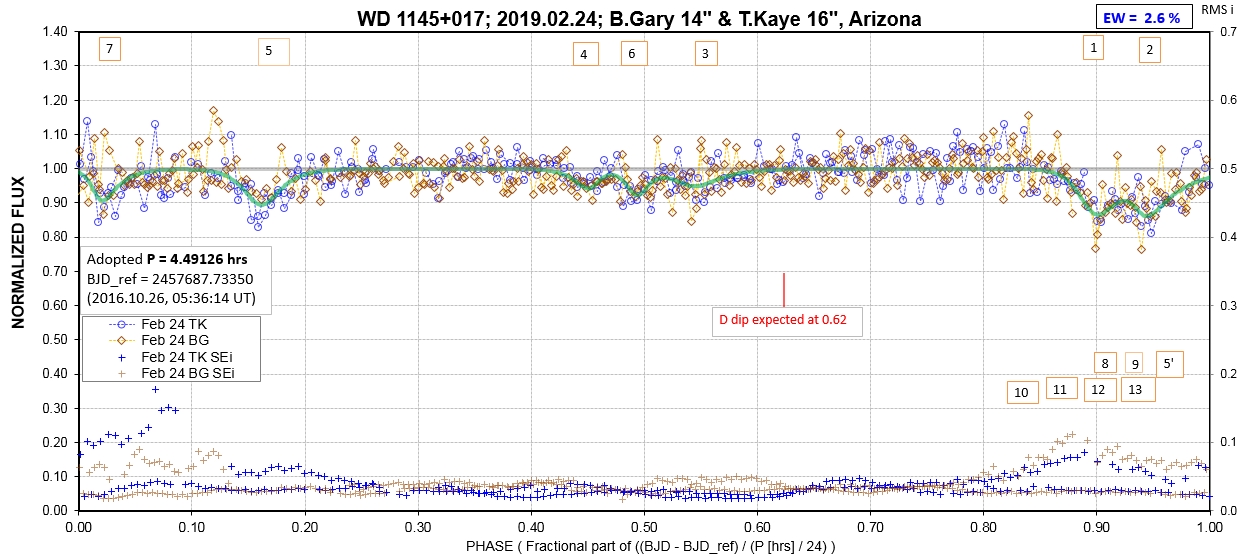
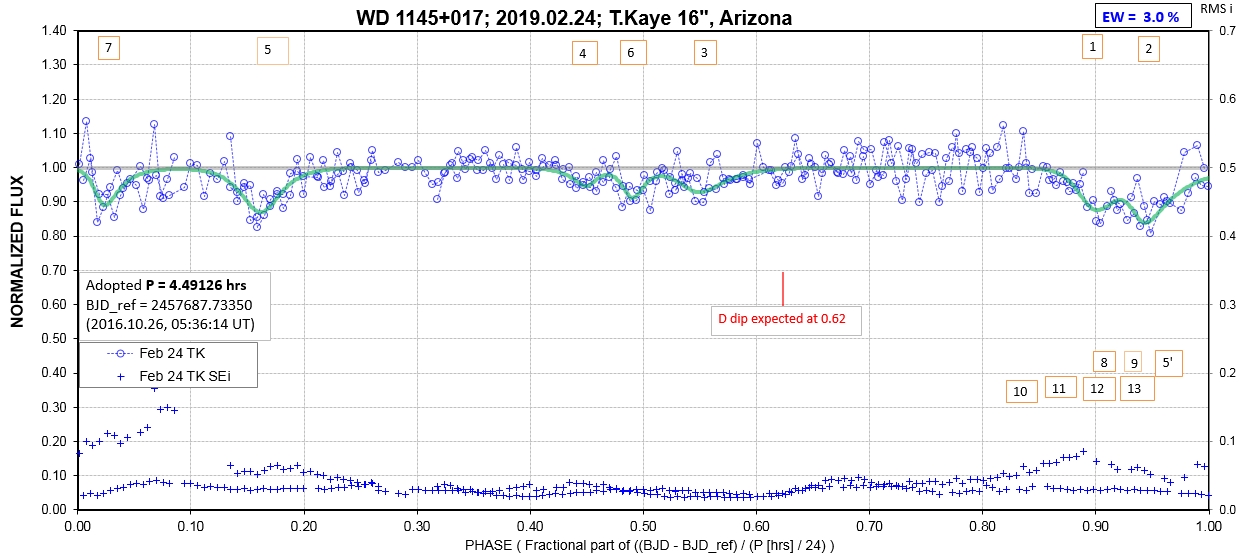
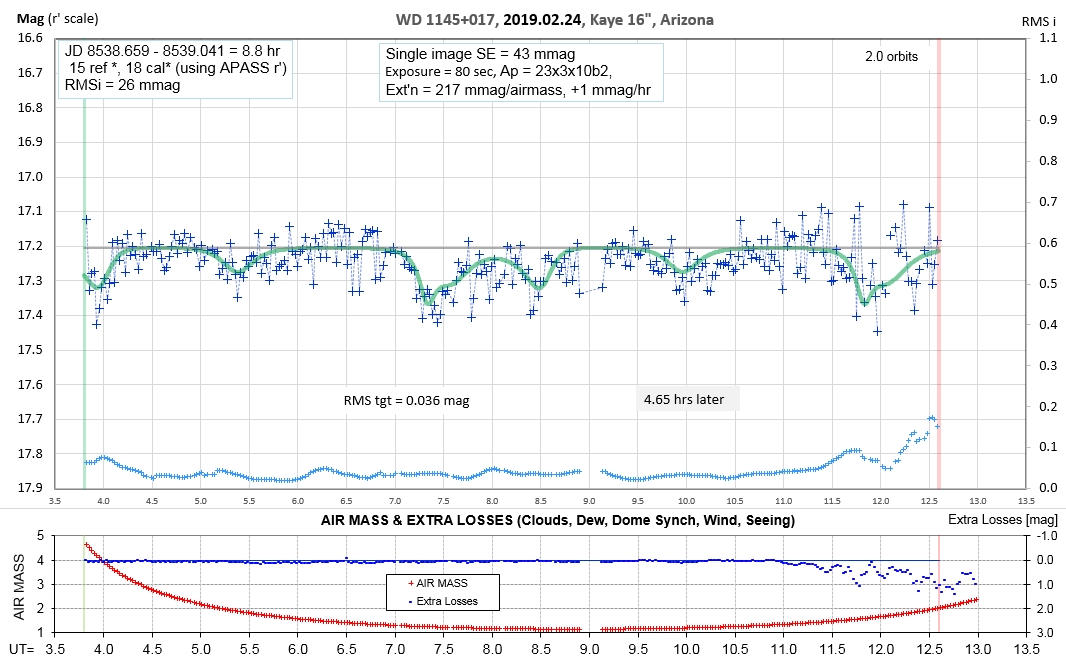
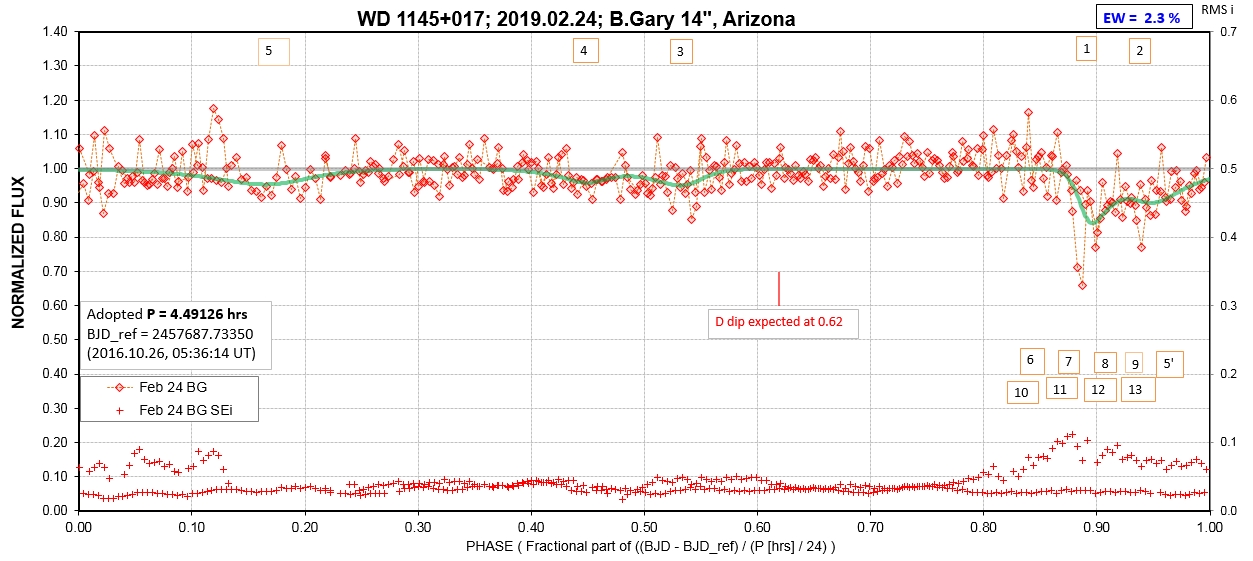
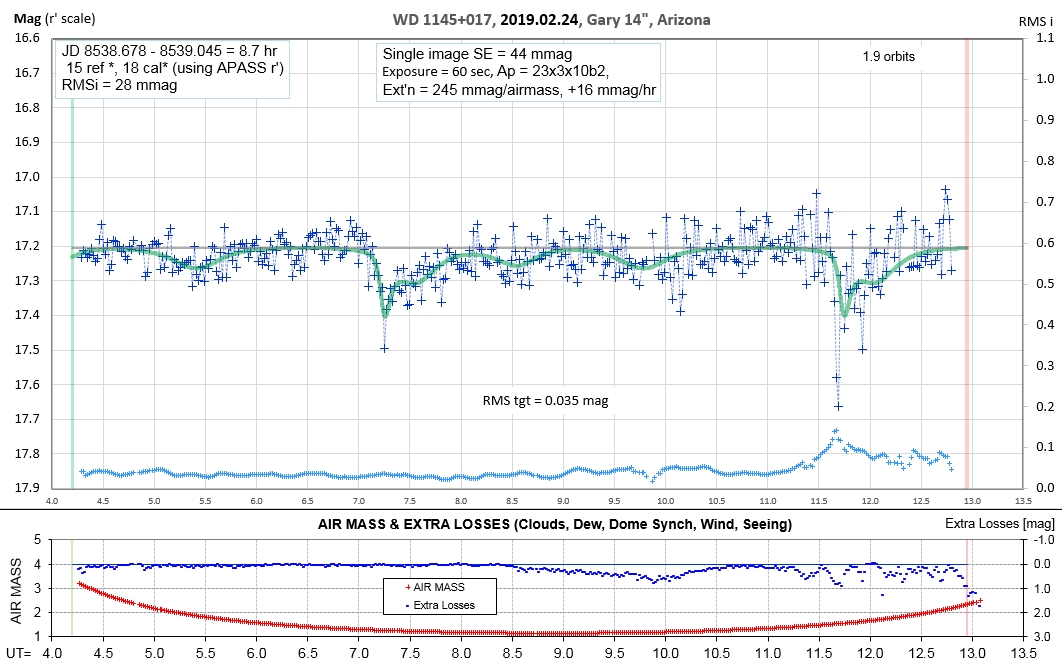
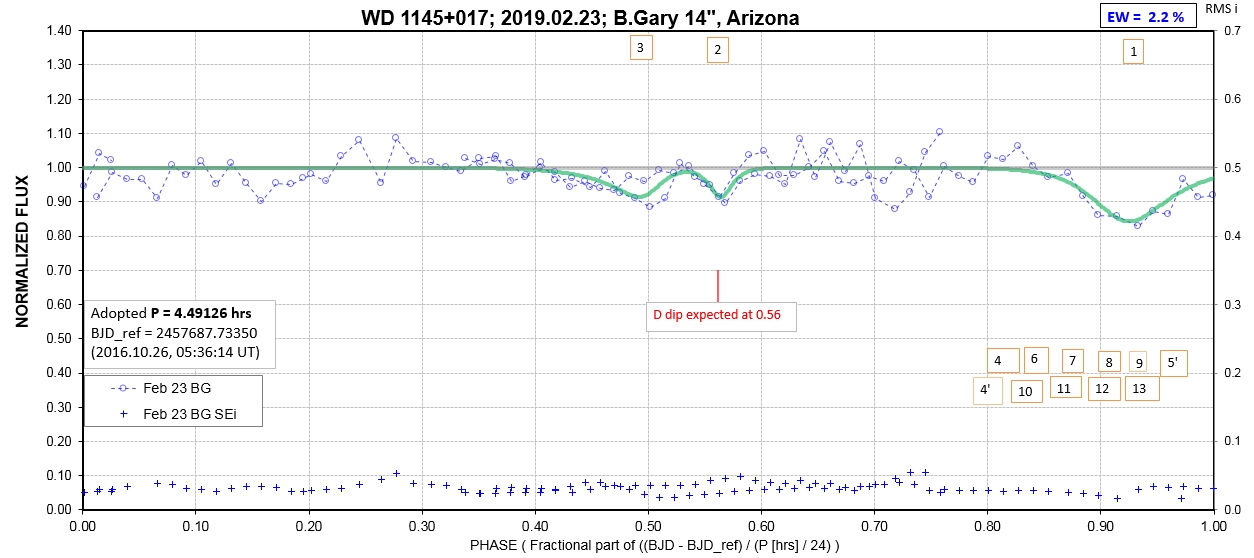
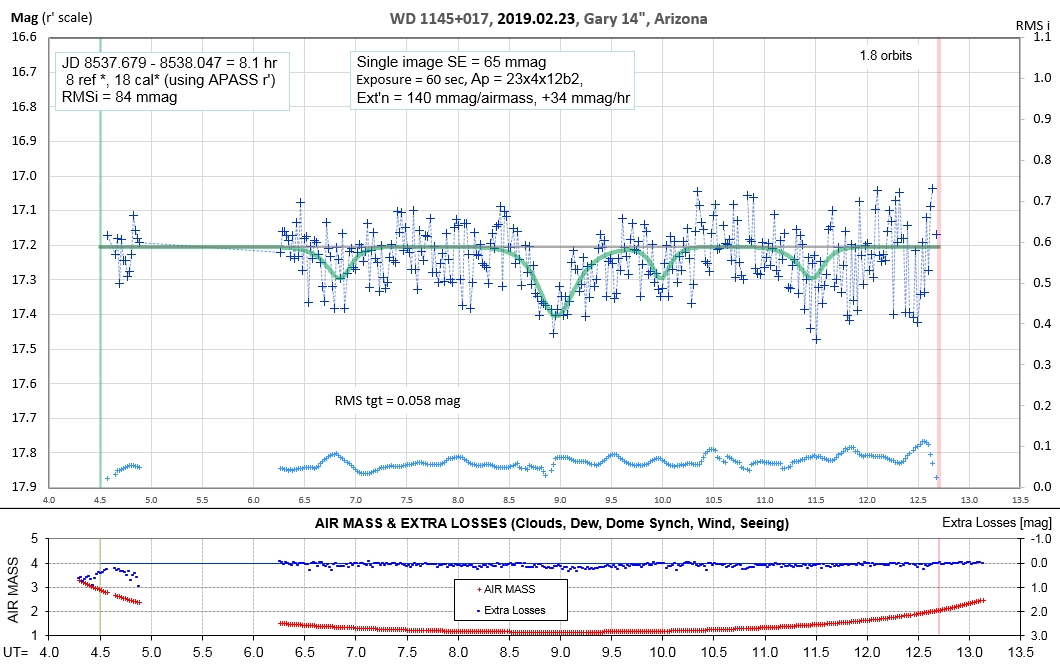
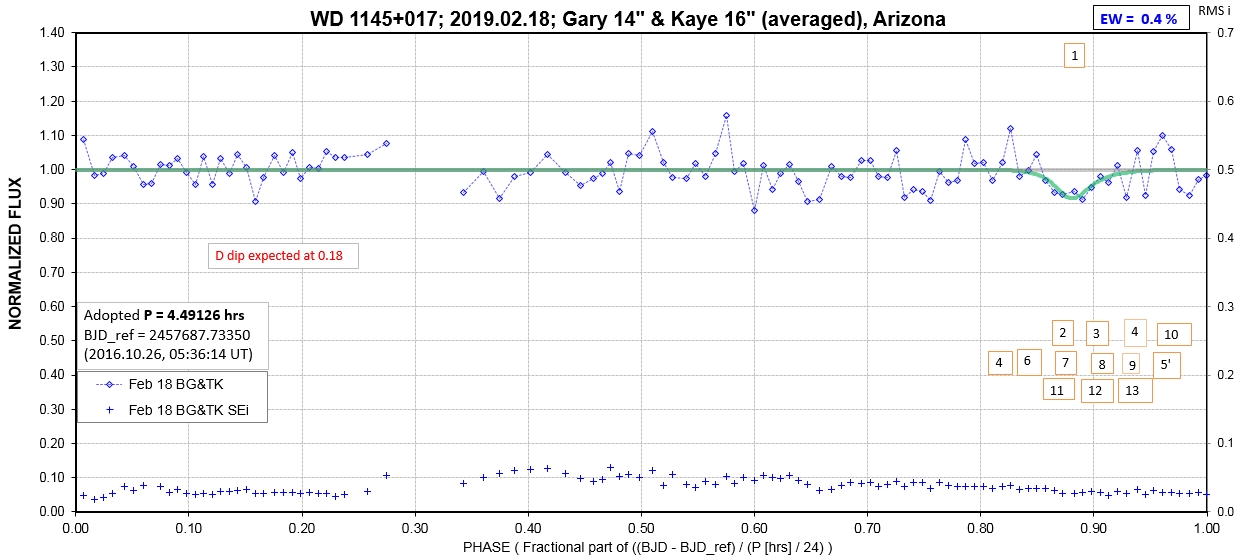
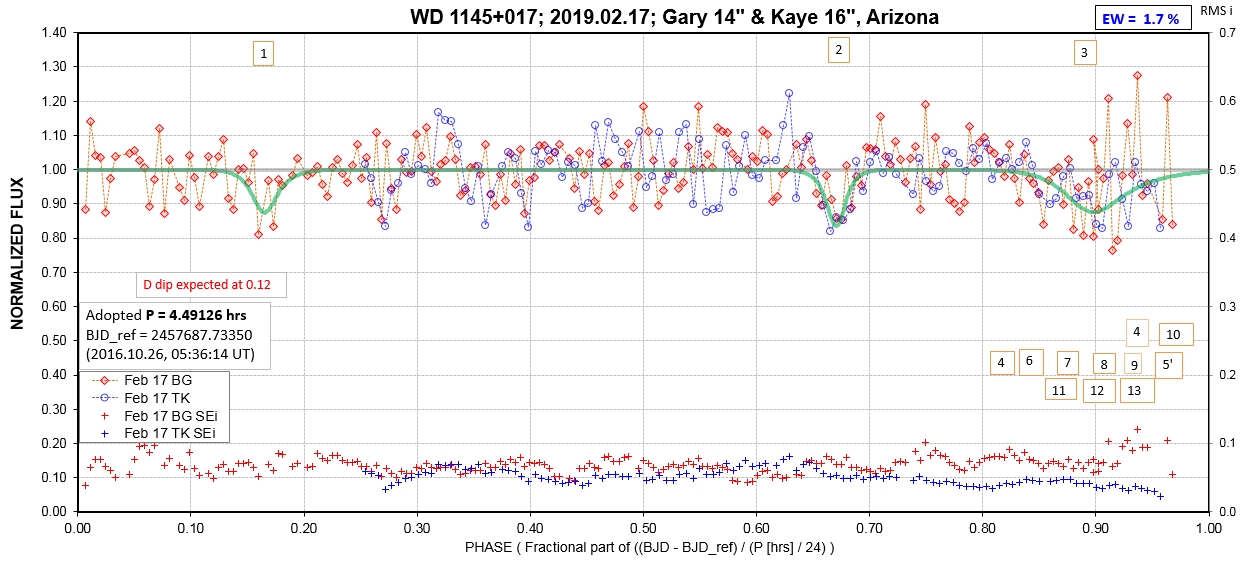
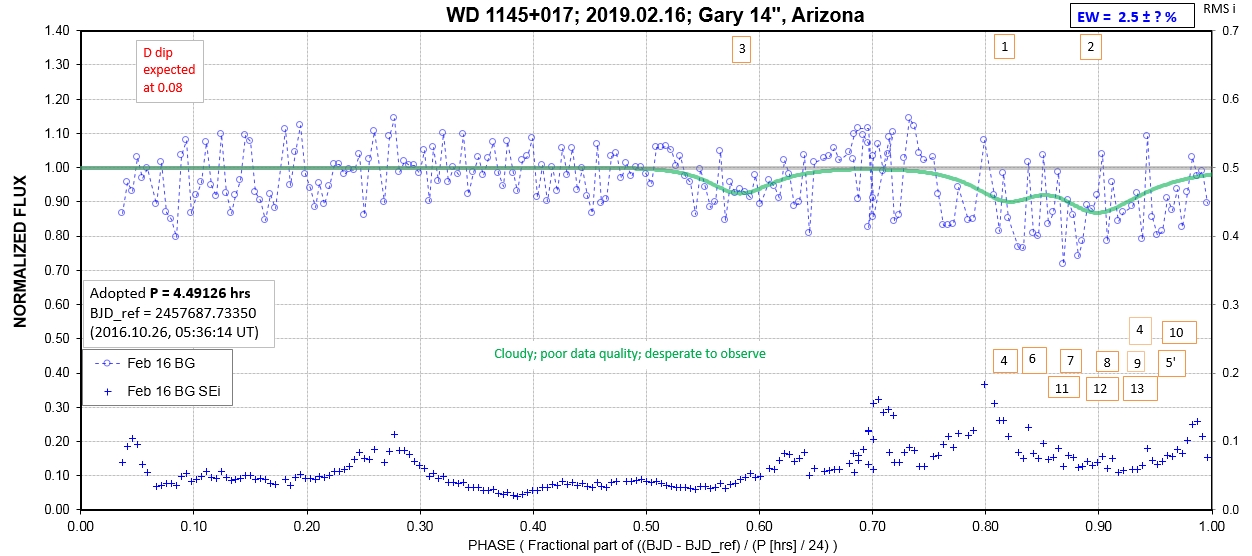
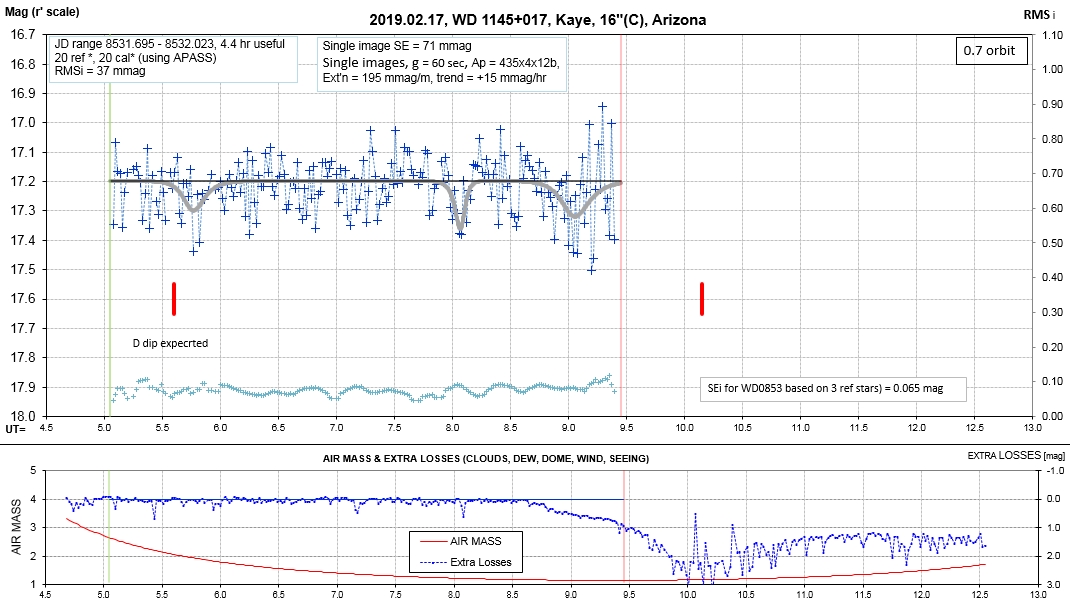
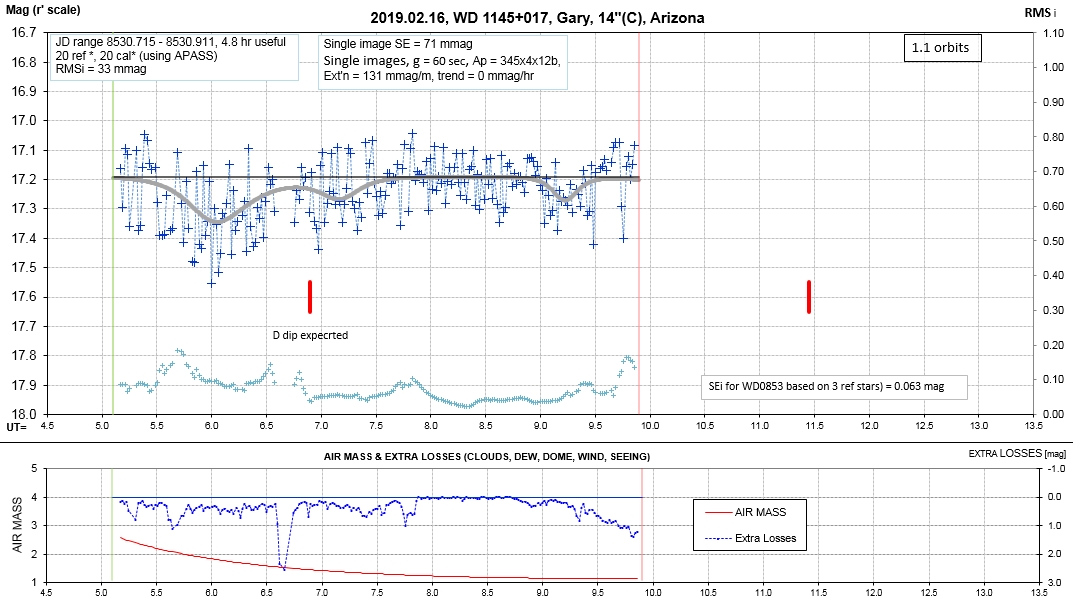
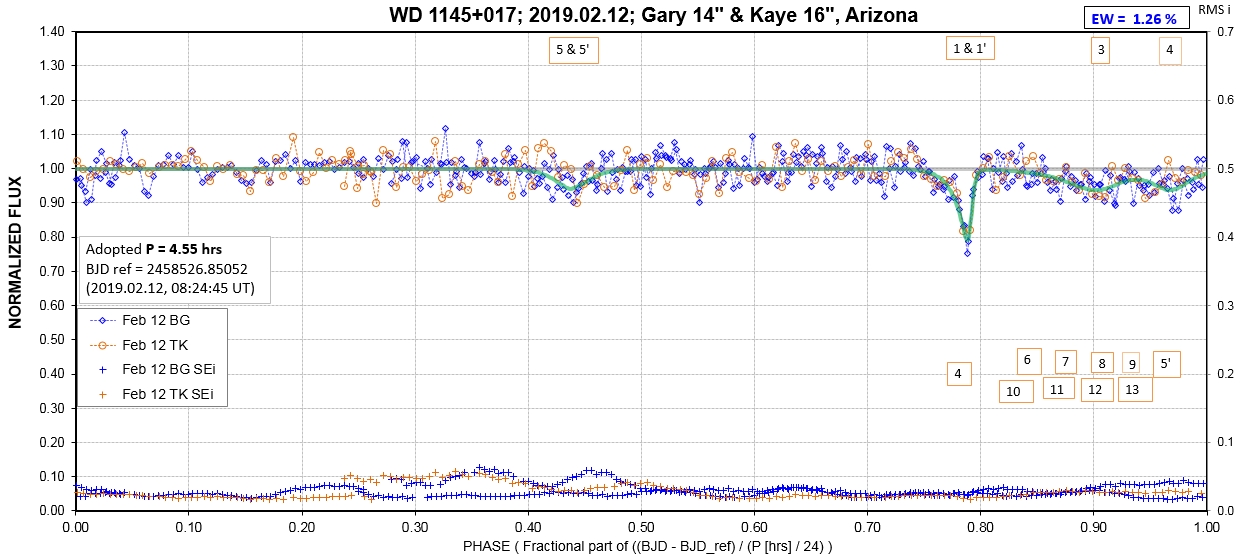
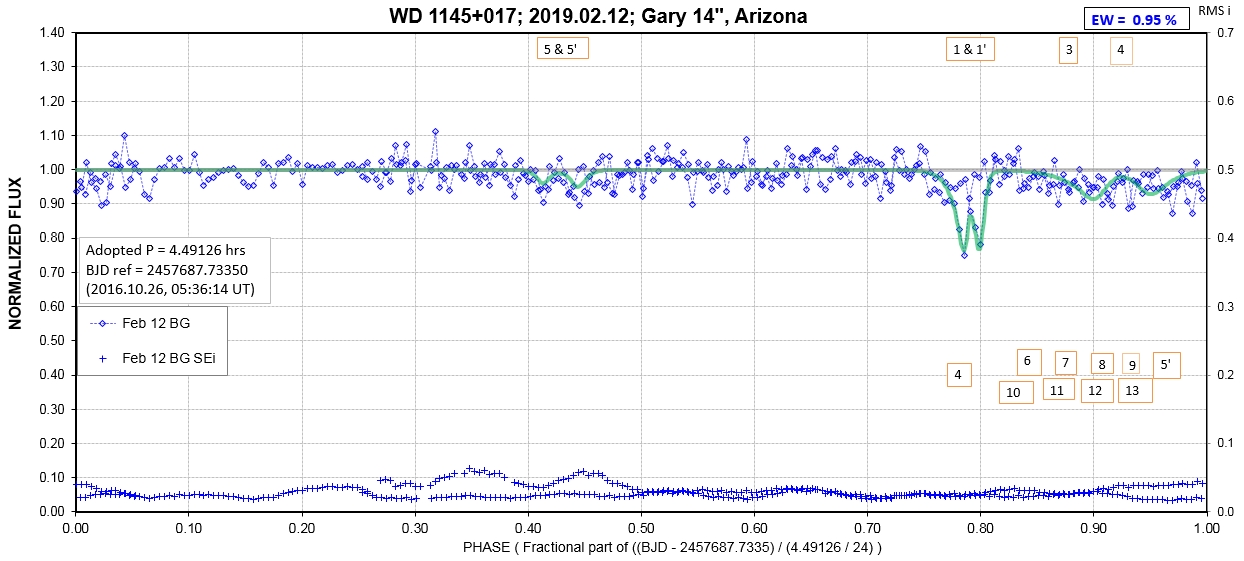
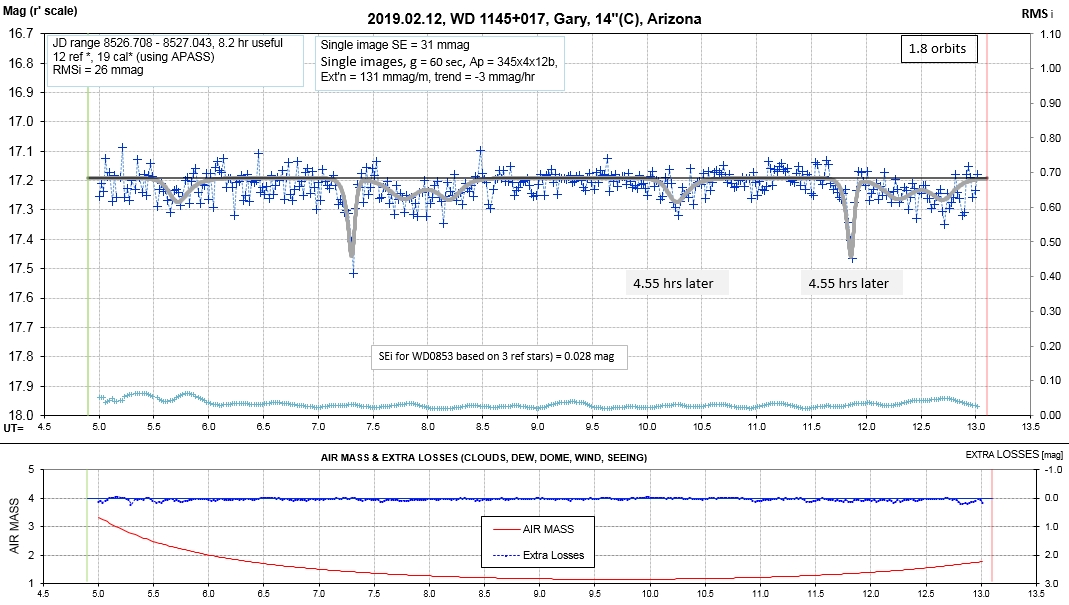
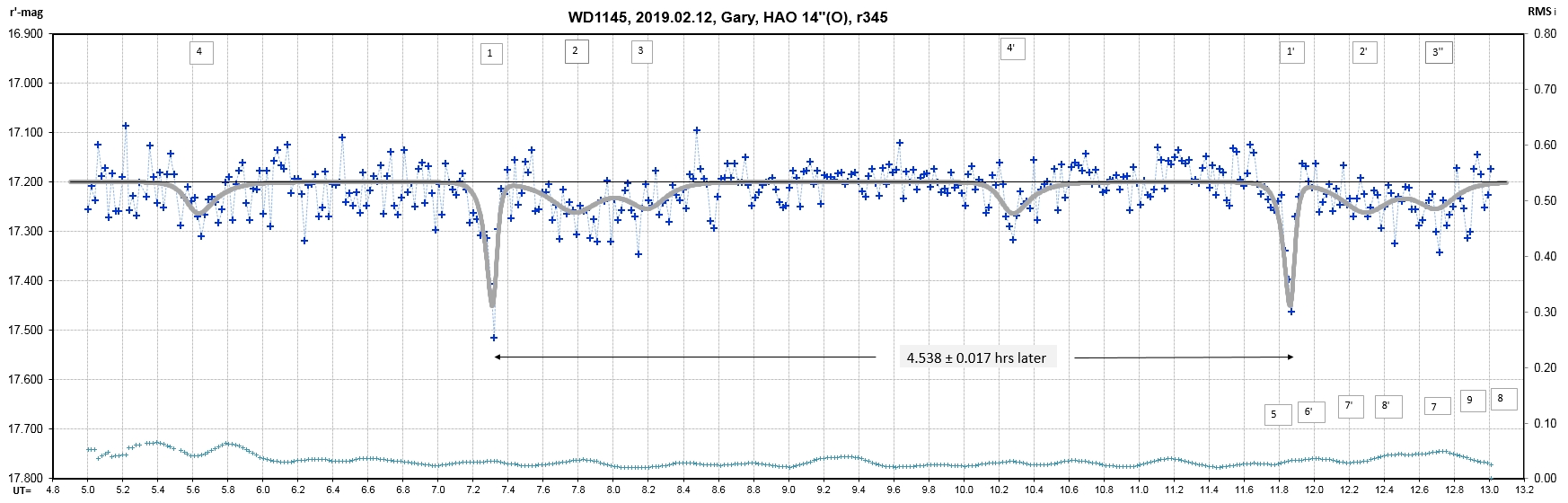
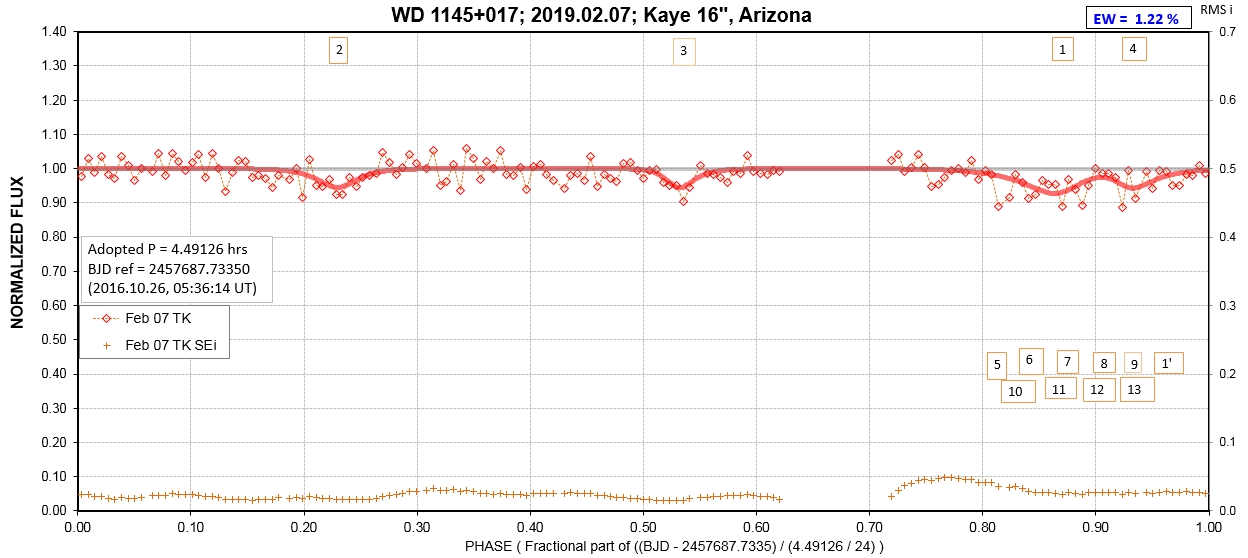
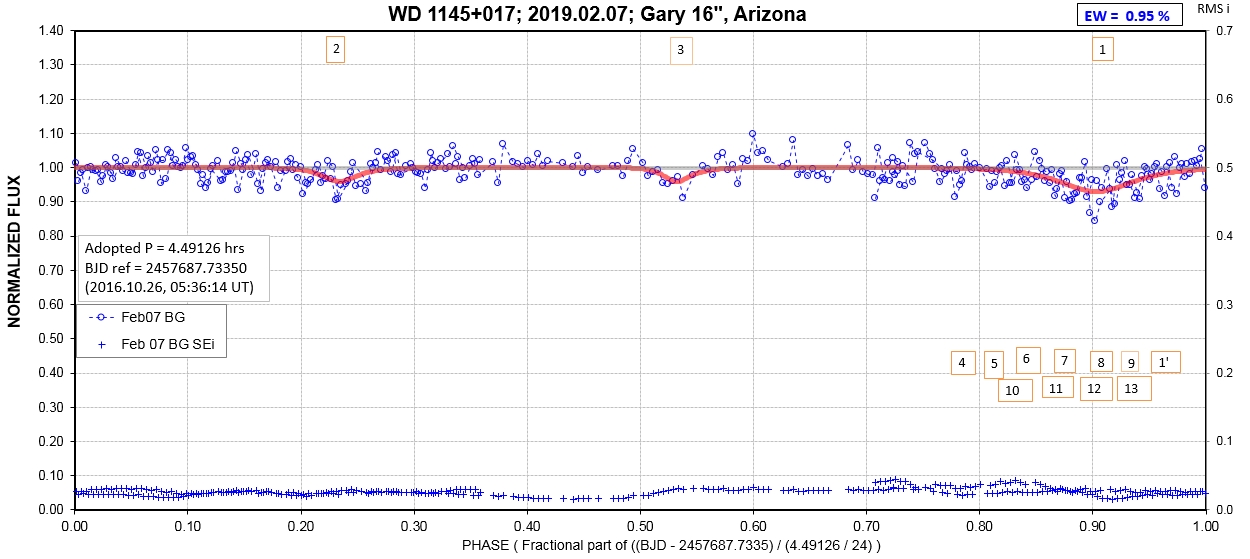
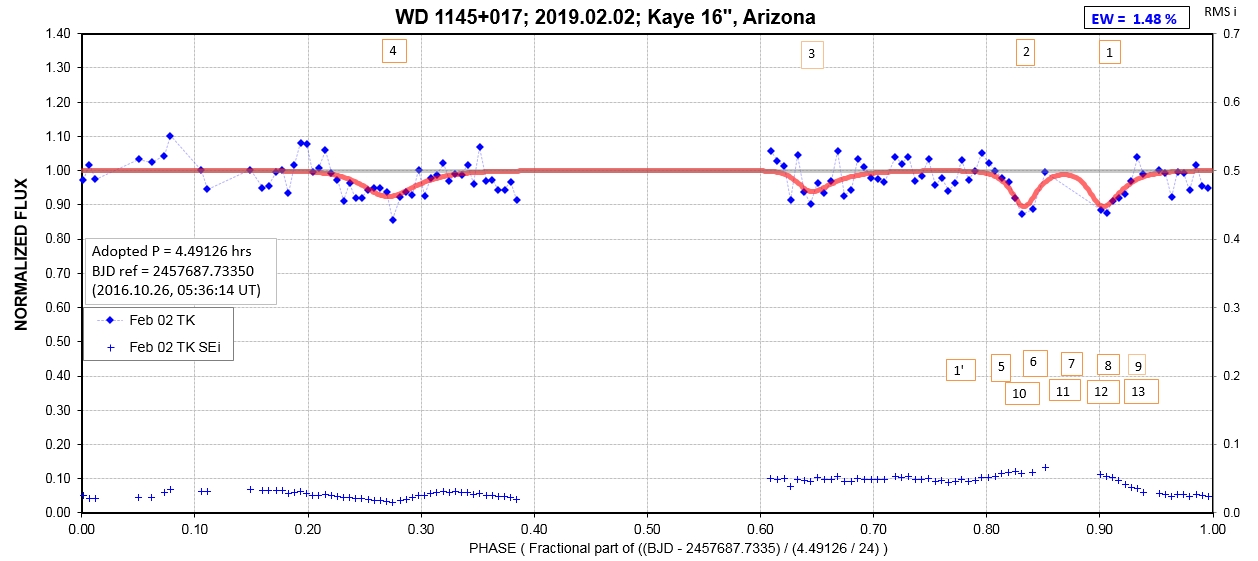
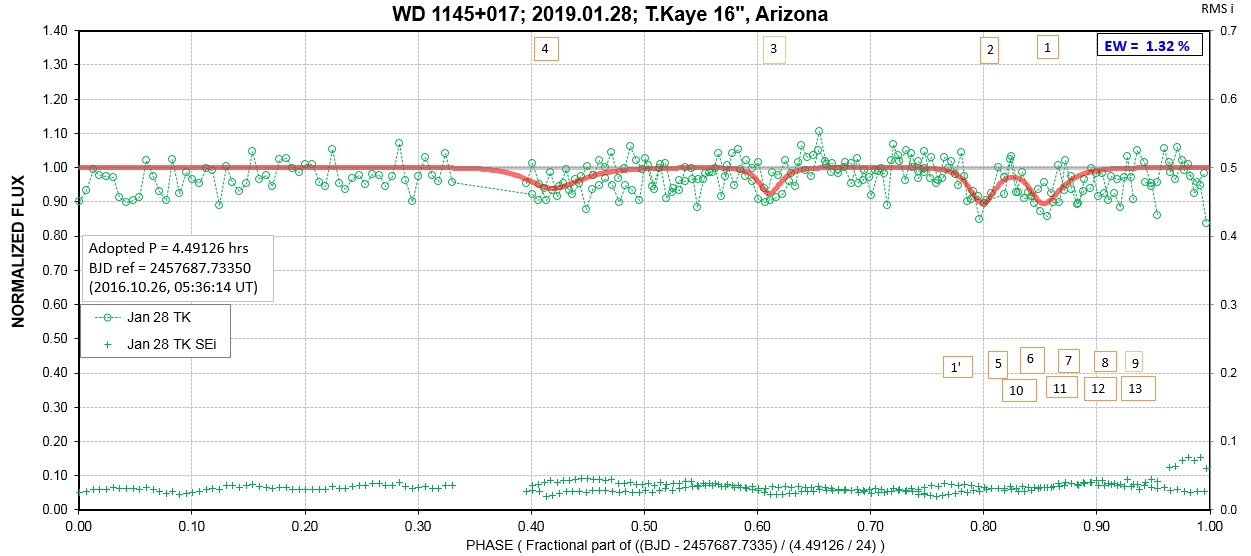
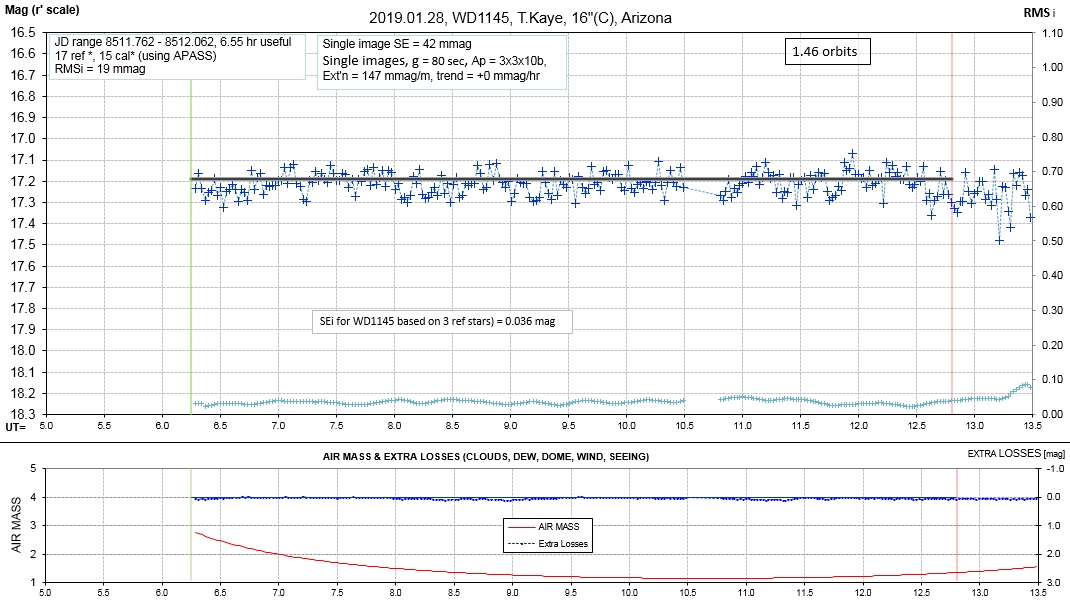
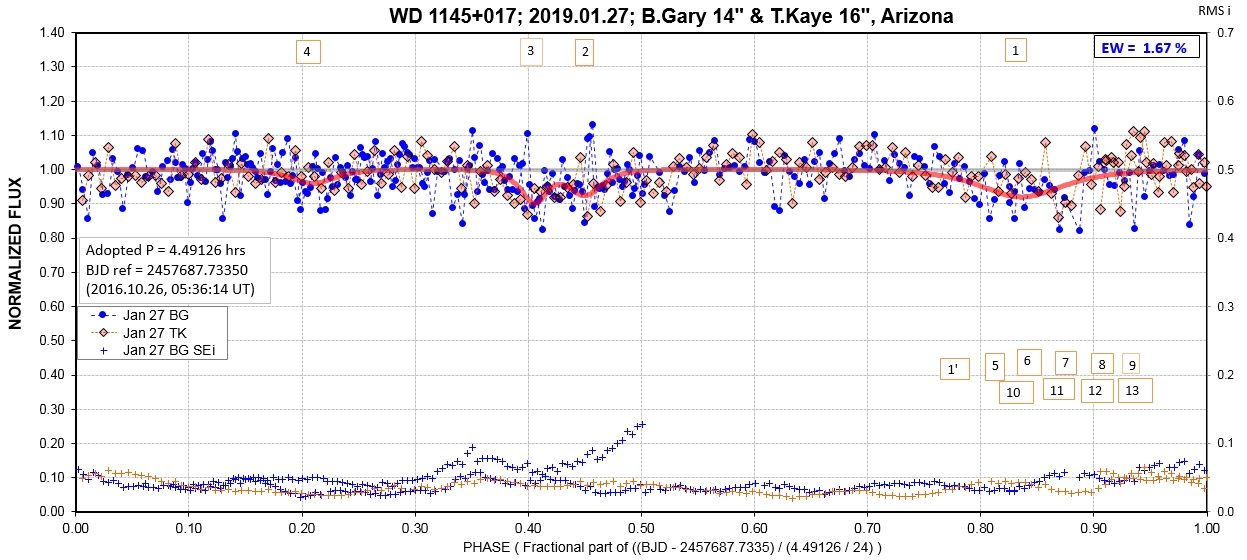
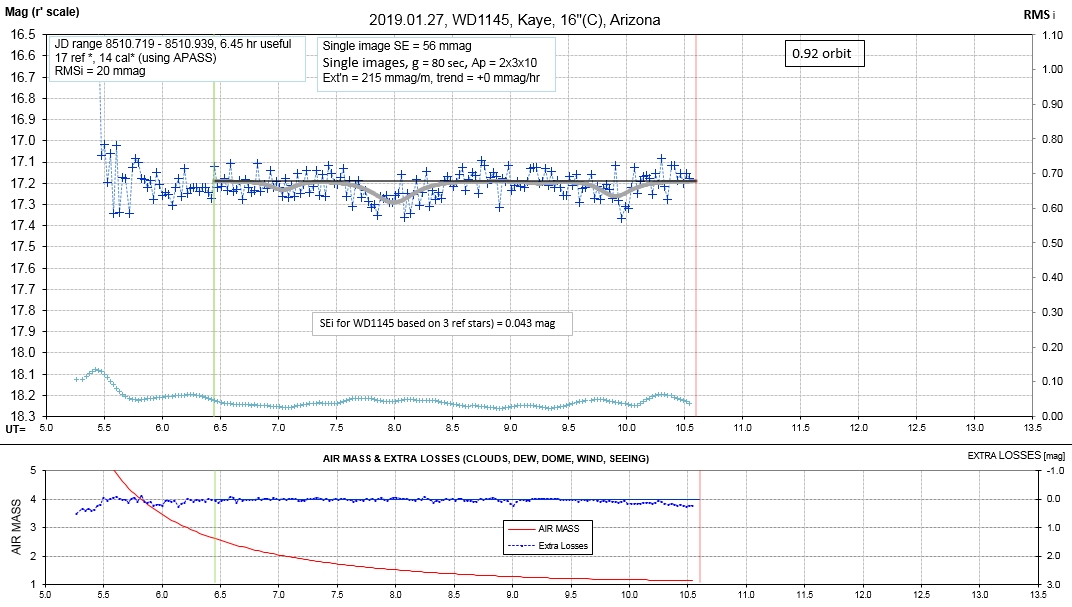
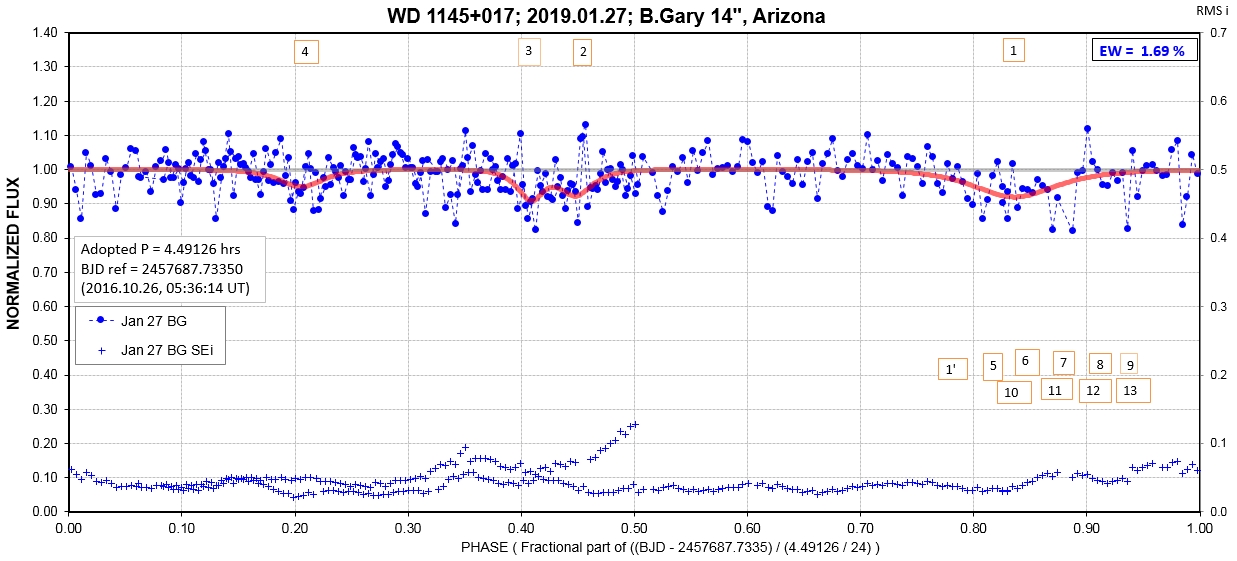
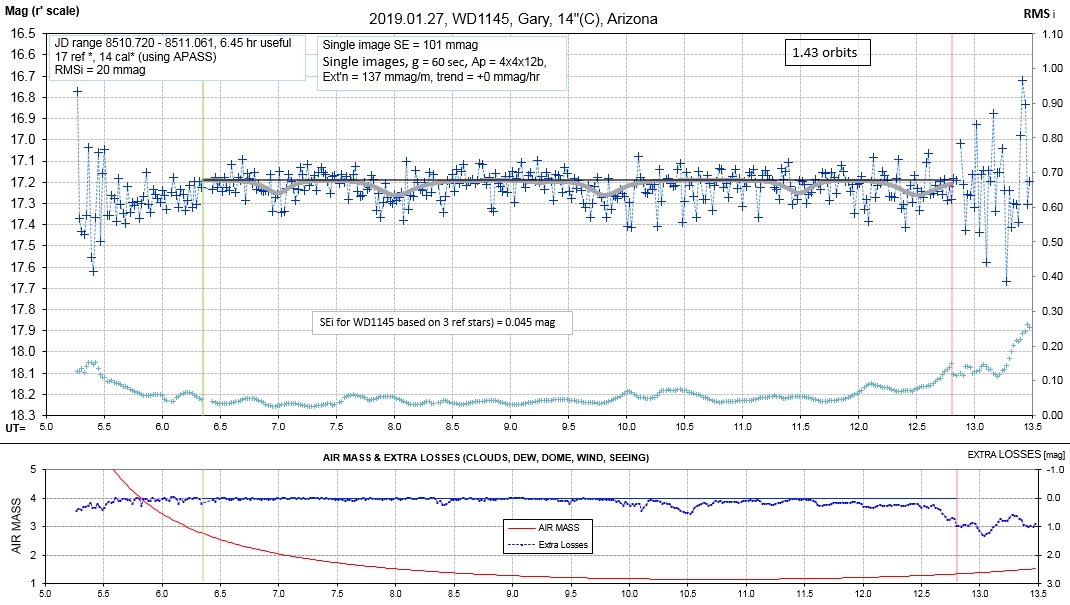
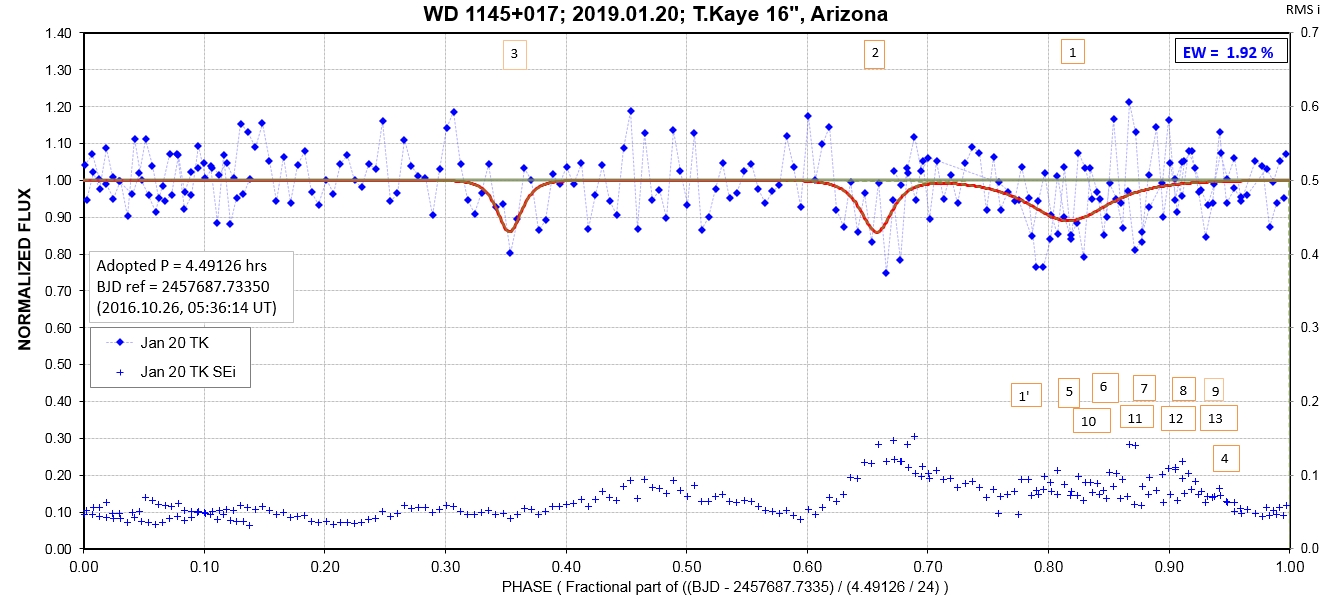
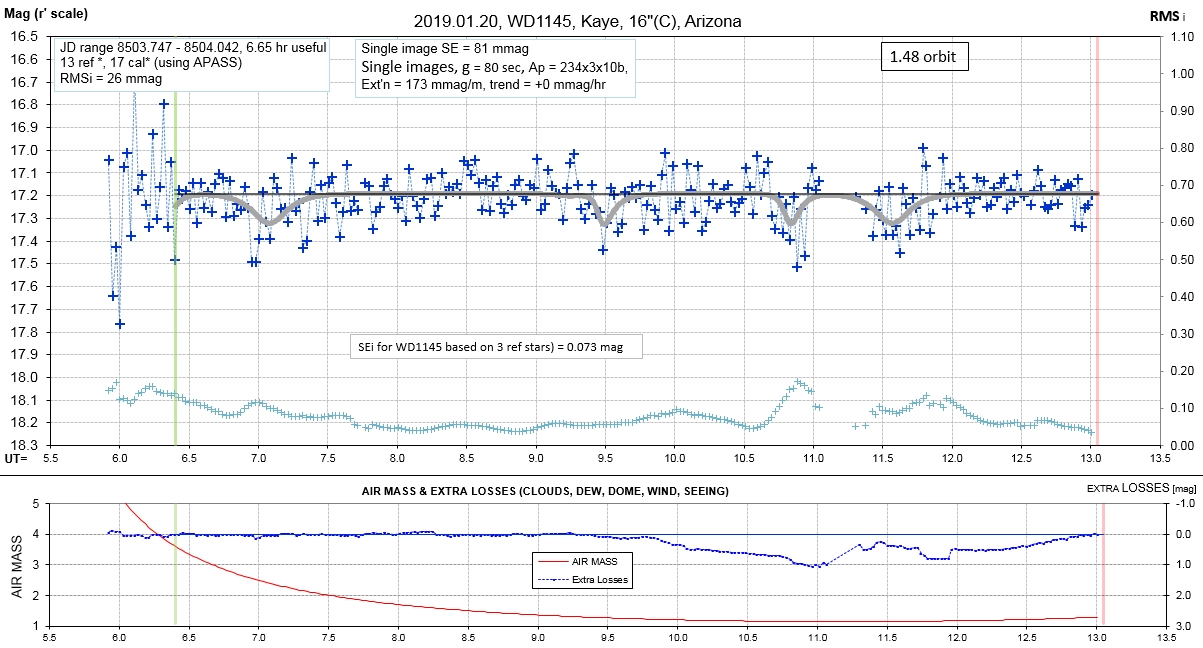
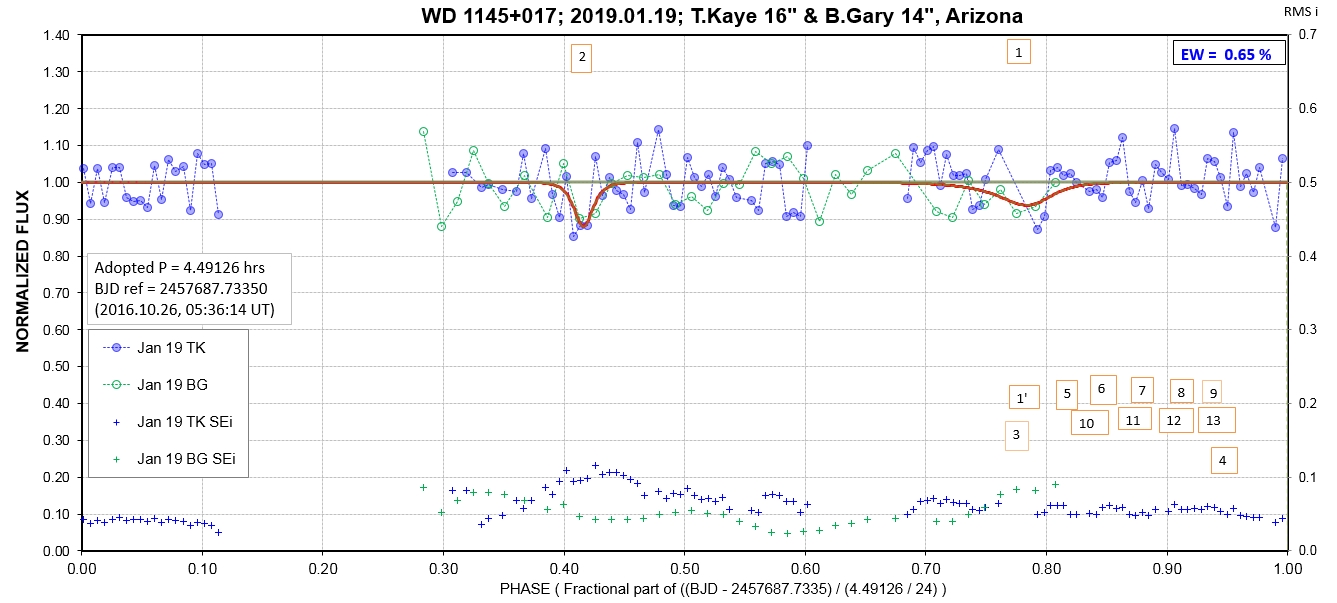
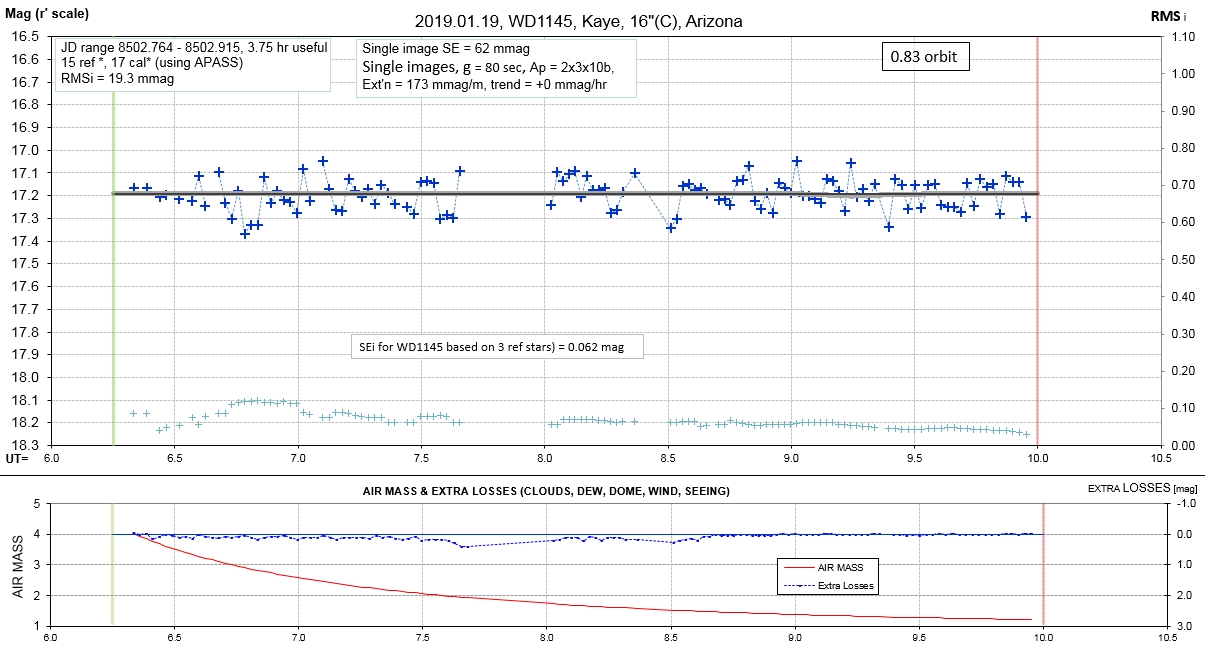
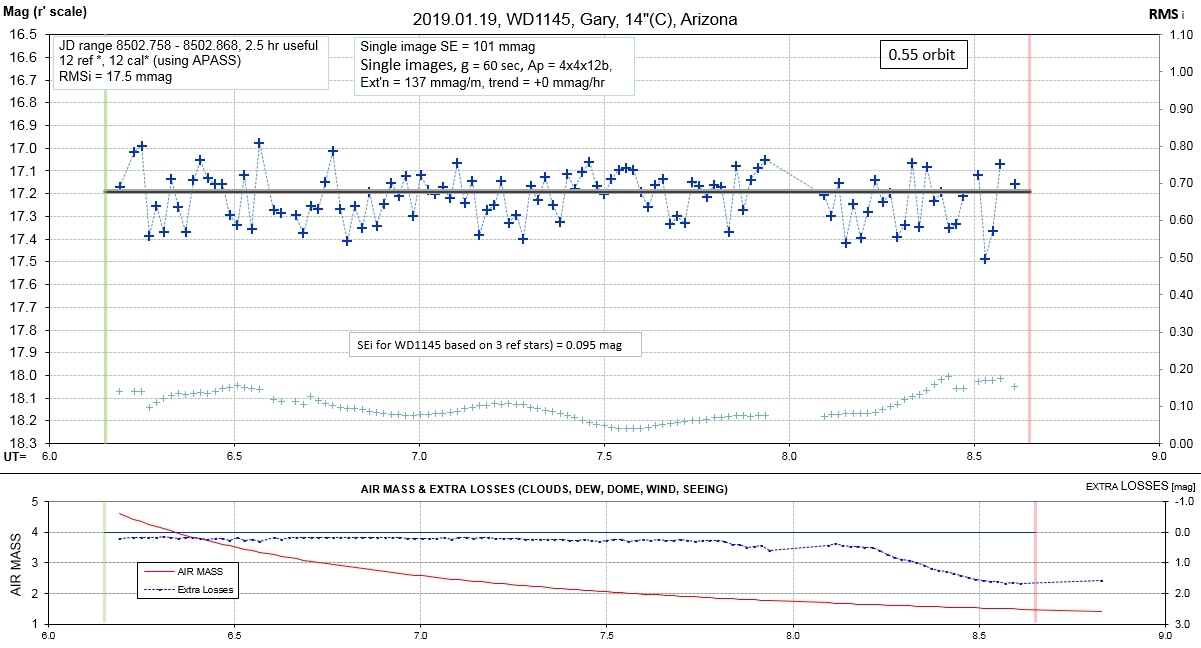
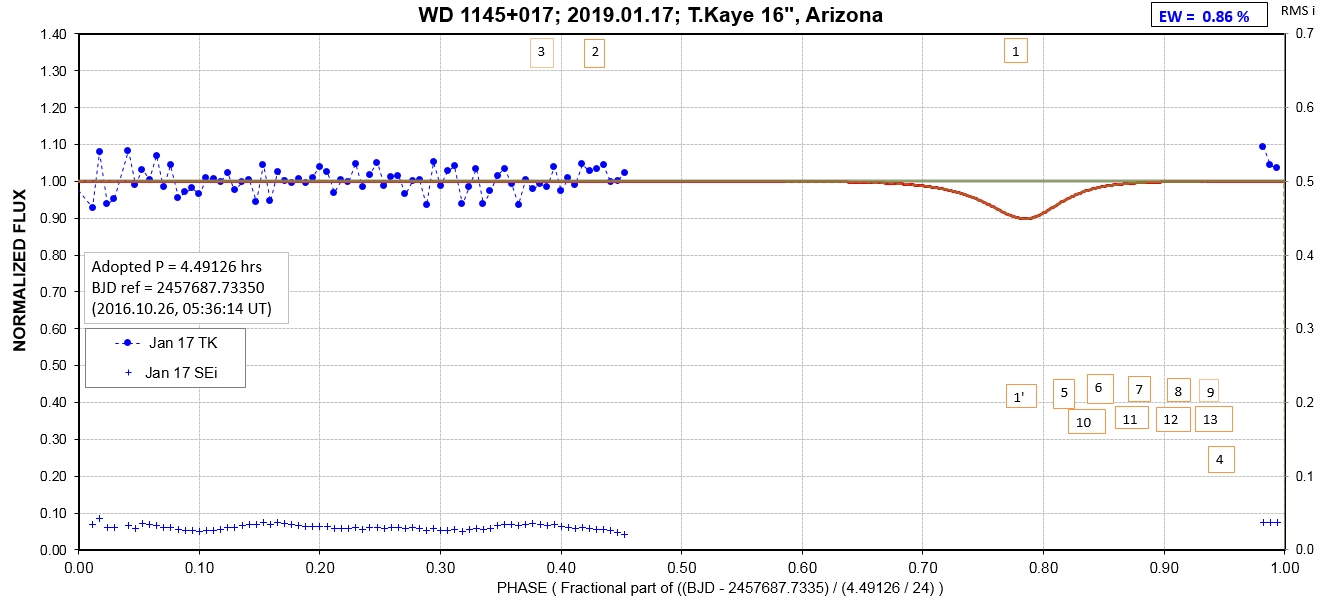
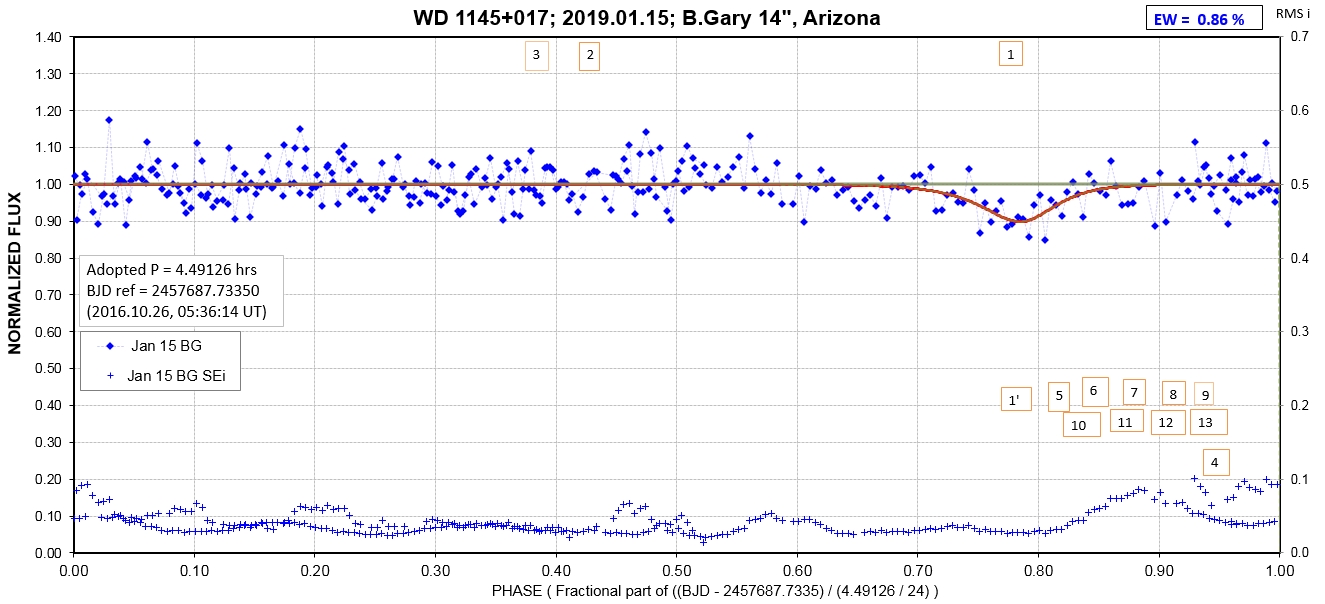
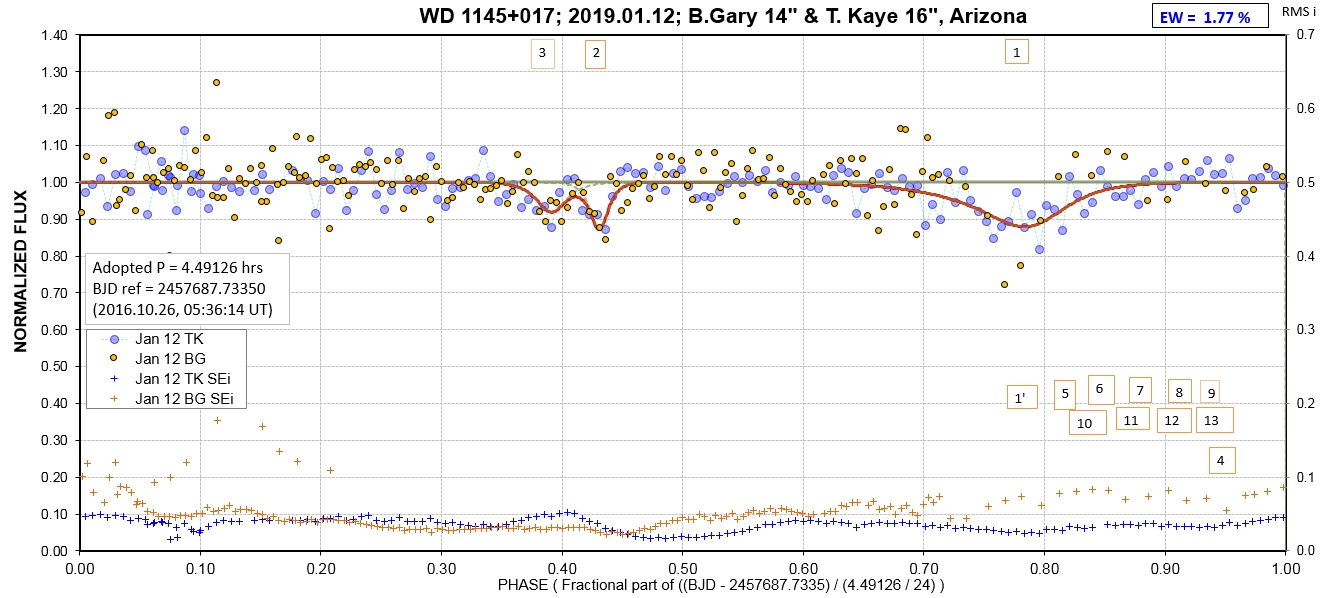
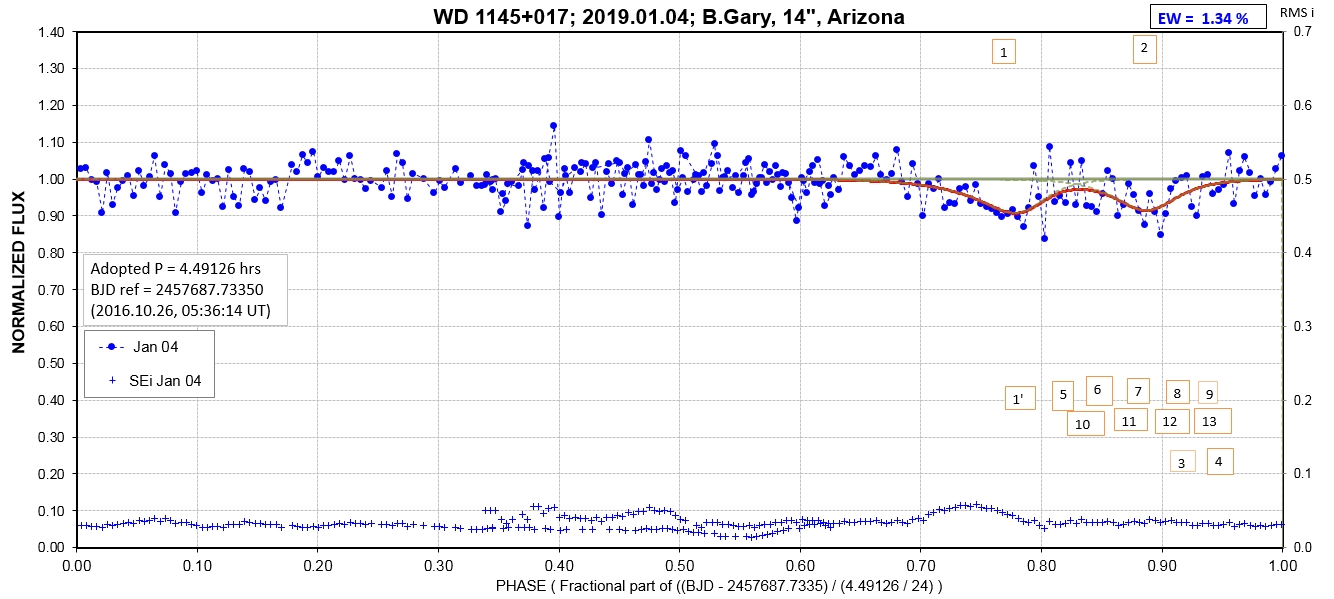
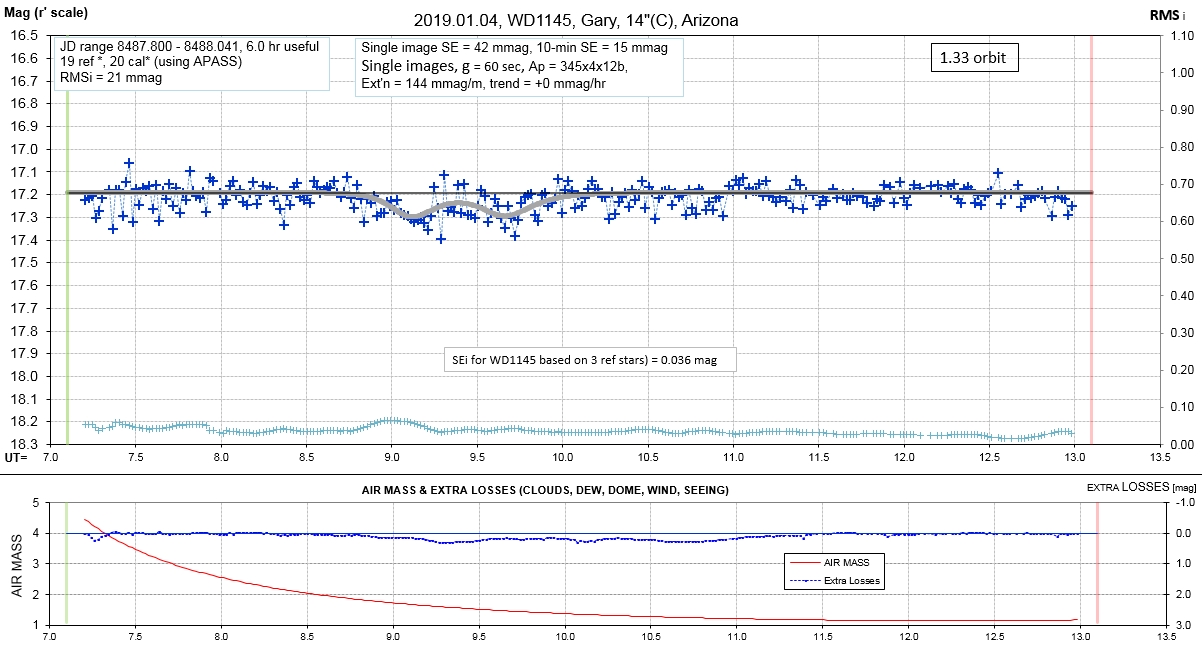
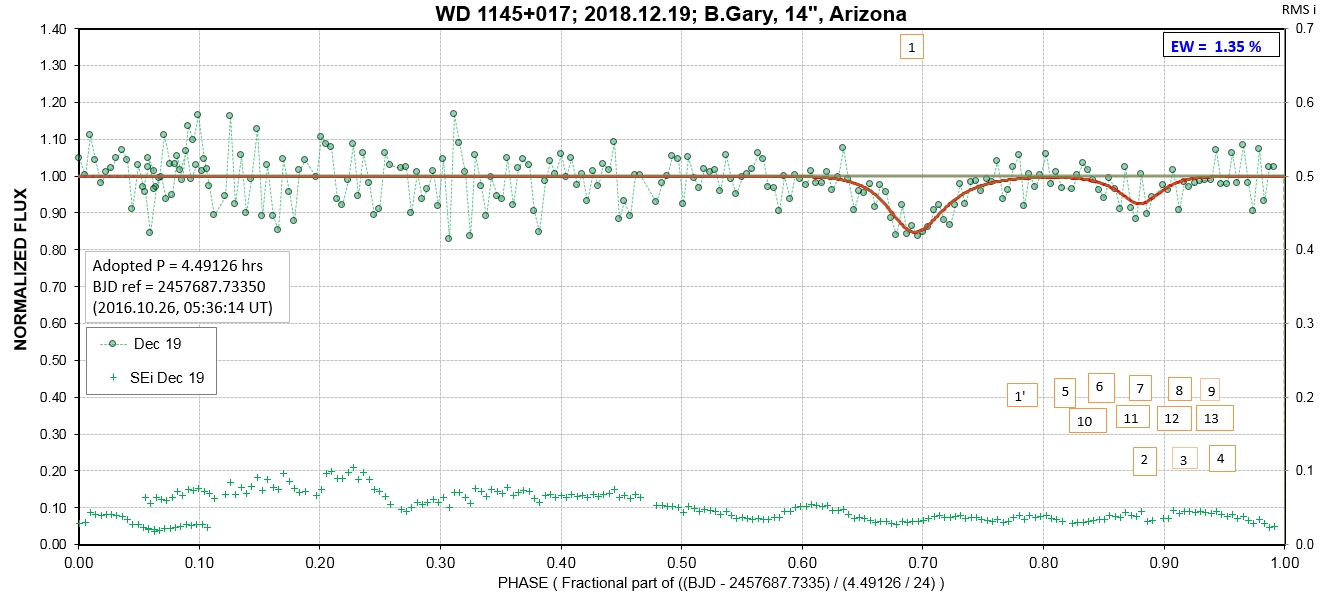
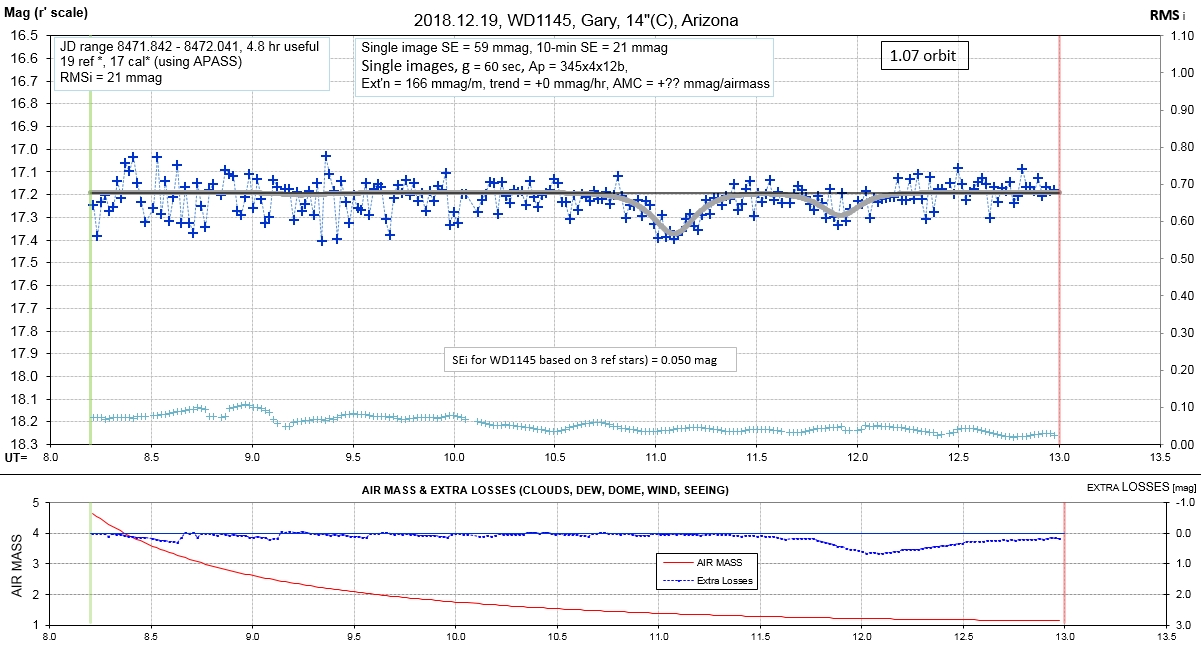
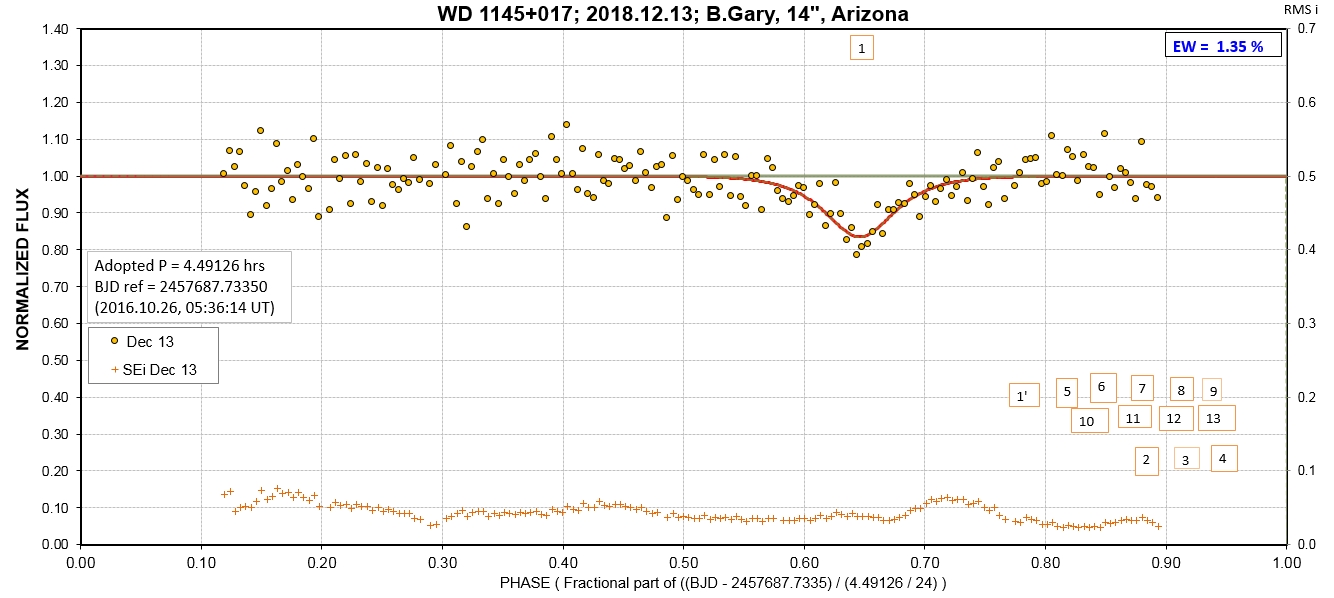
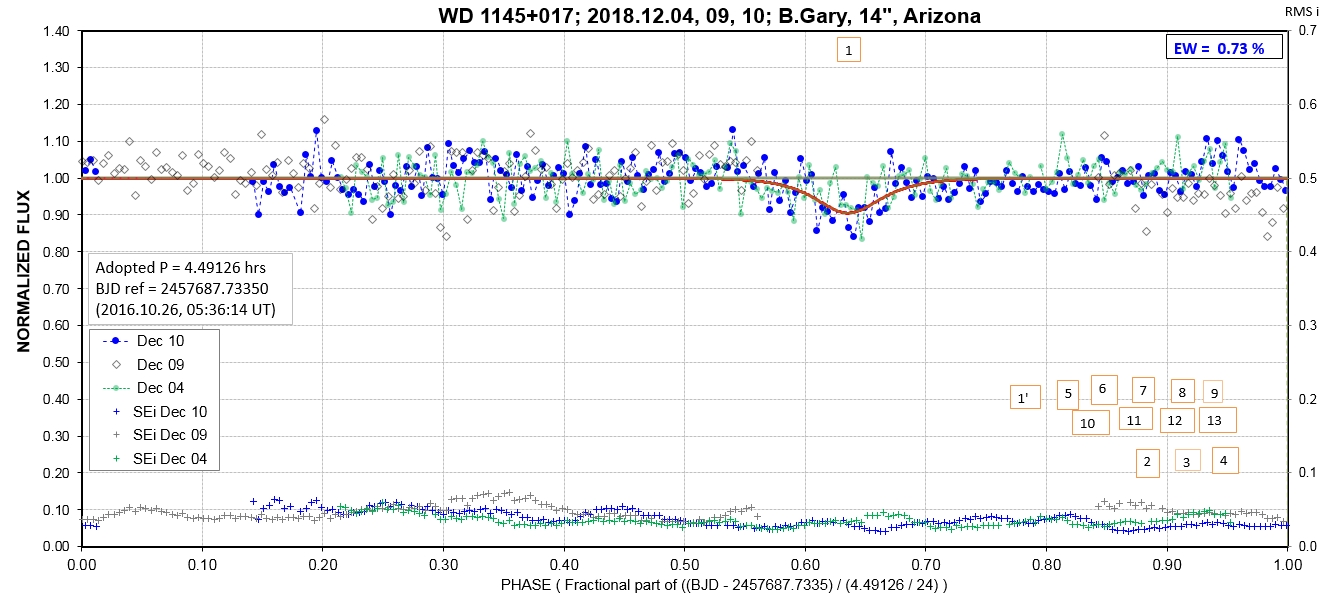
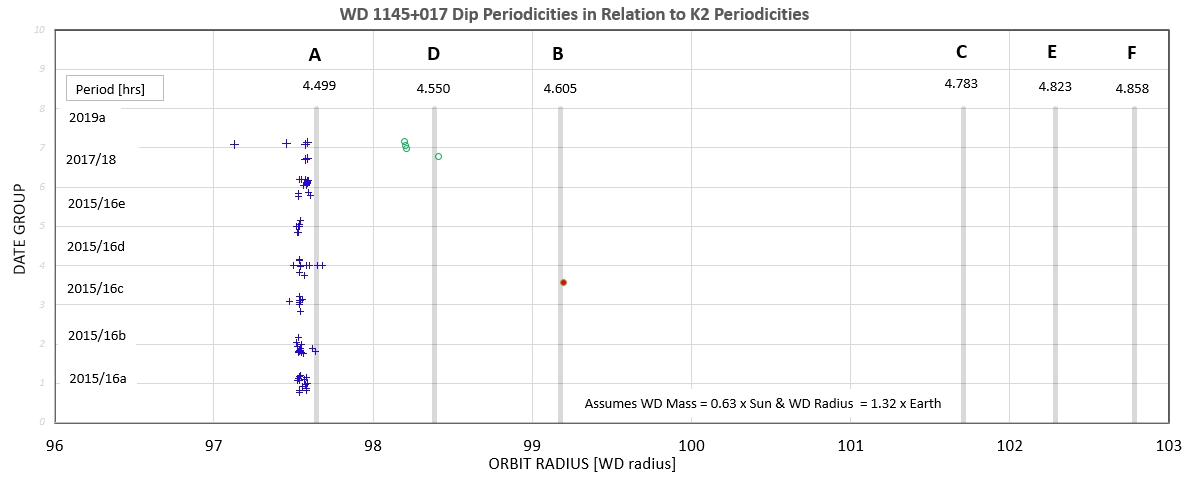
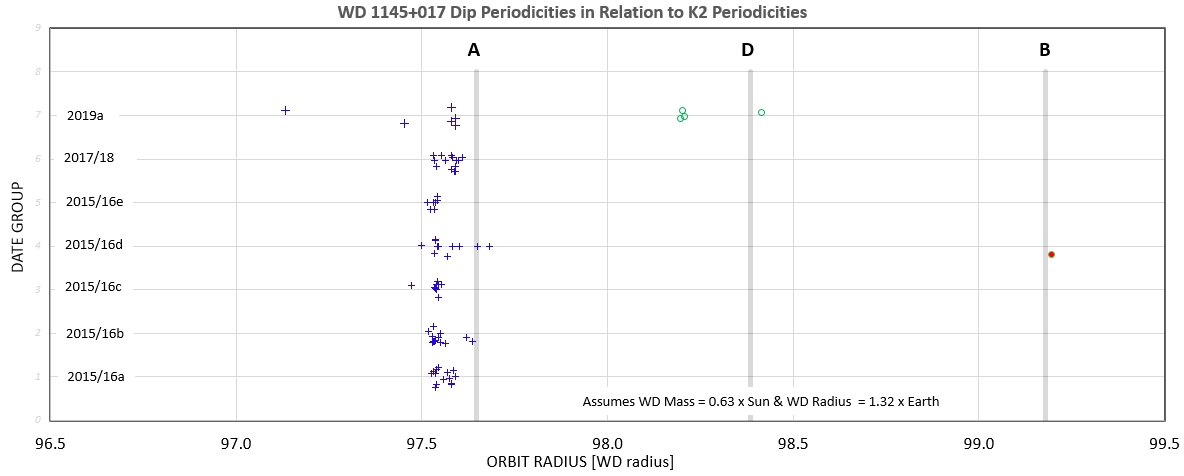
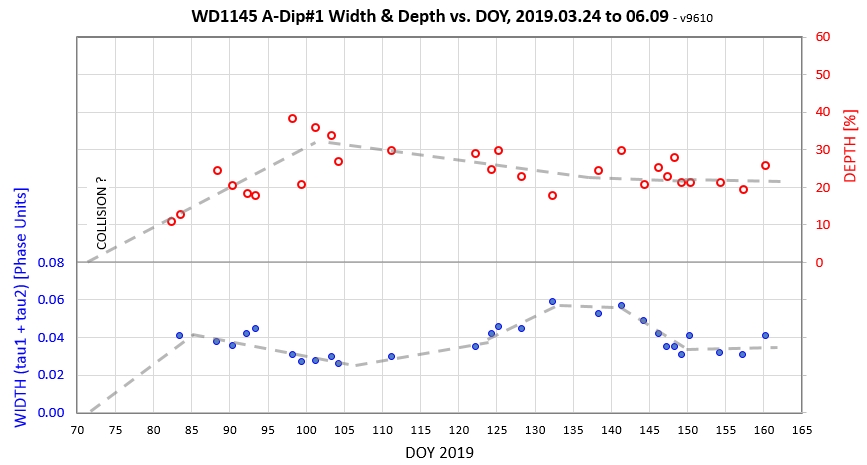
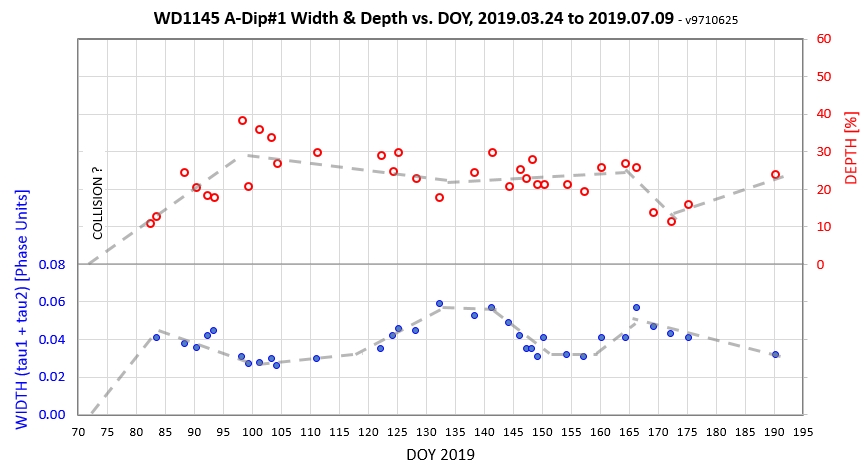
The following sequence of phase-folded light curves can be used to study the recent evolution of all dip activity.









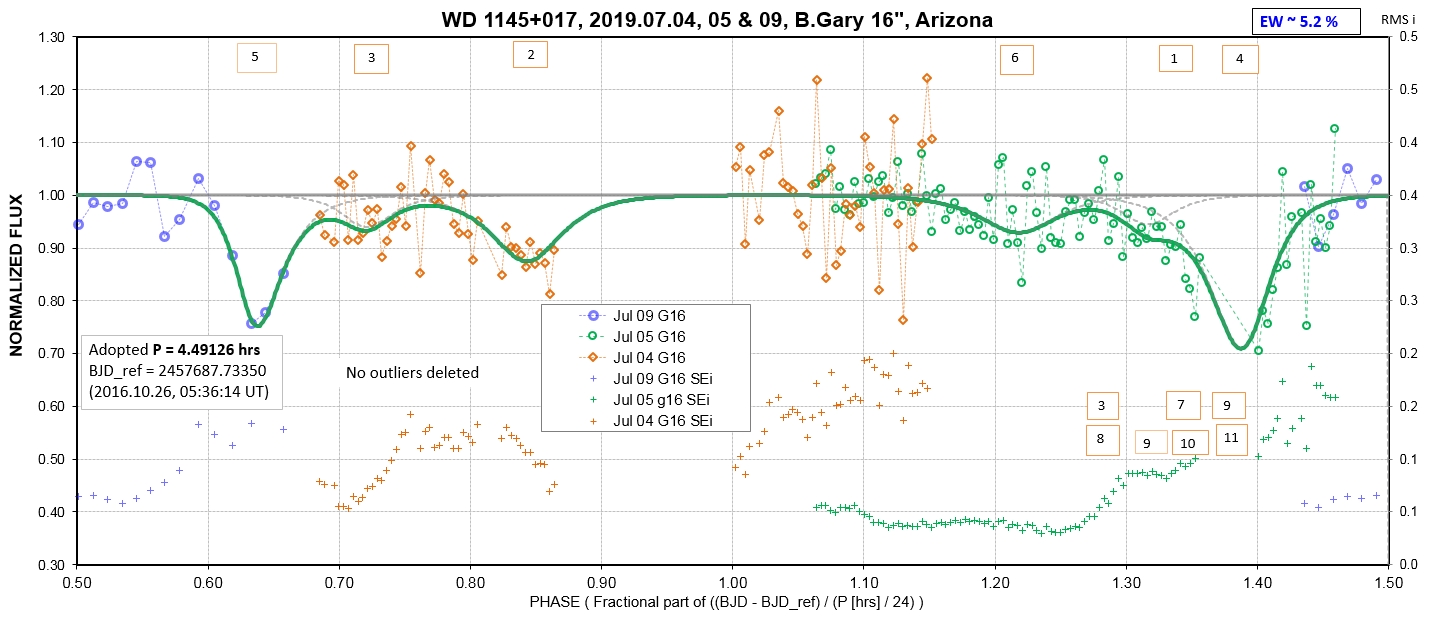
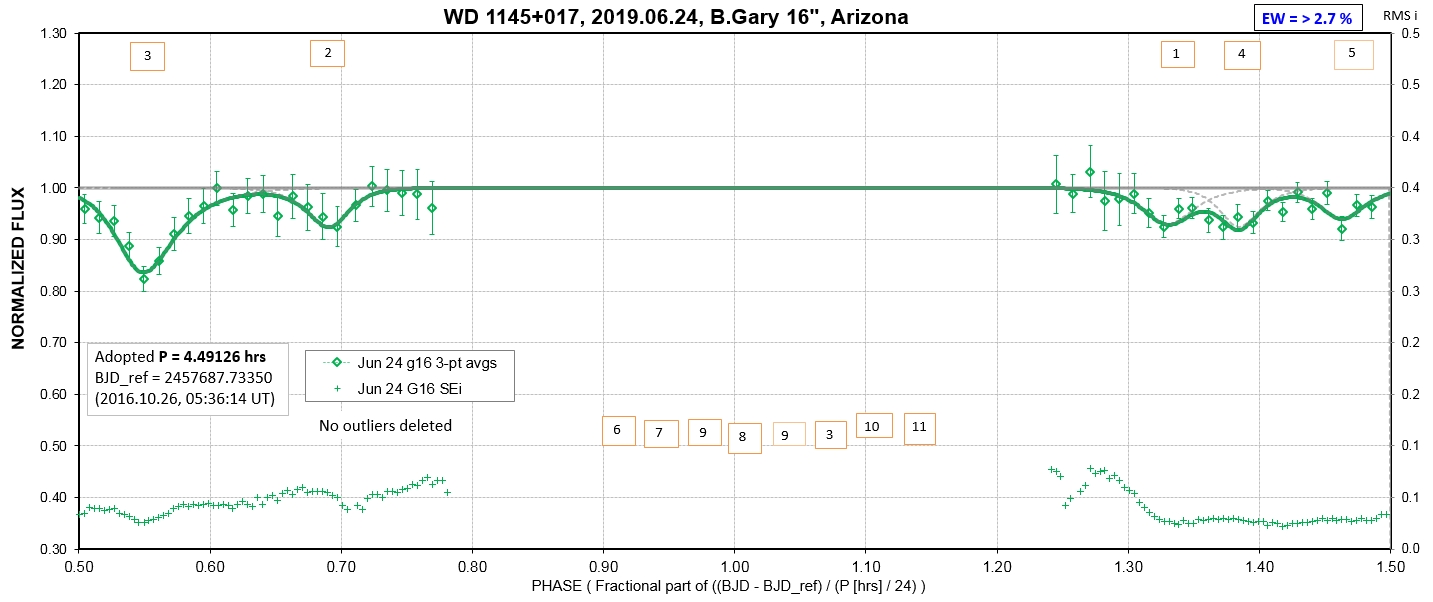
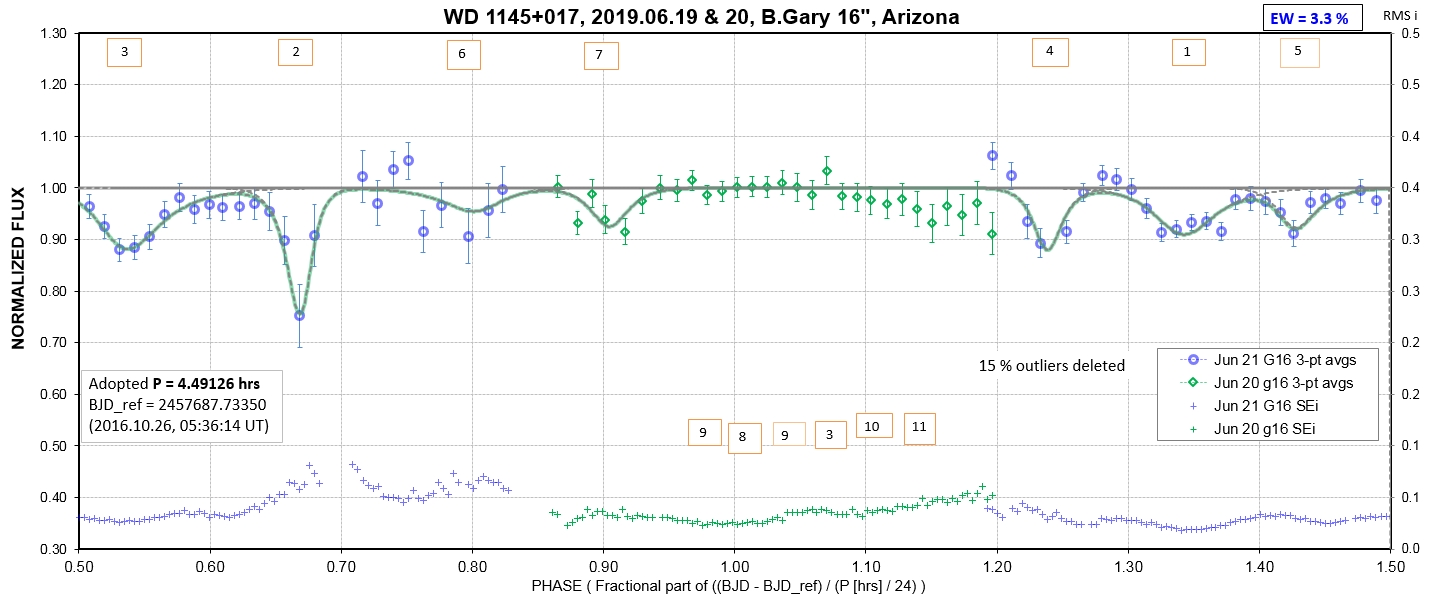
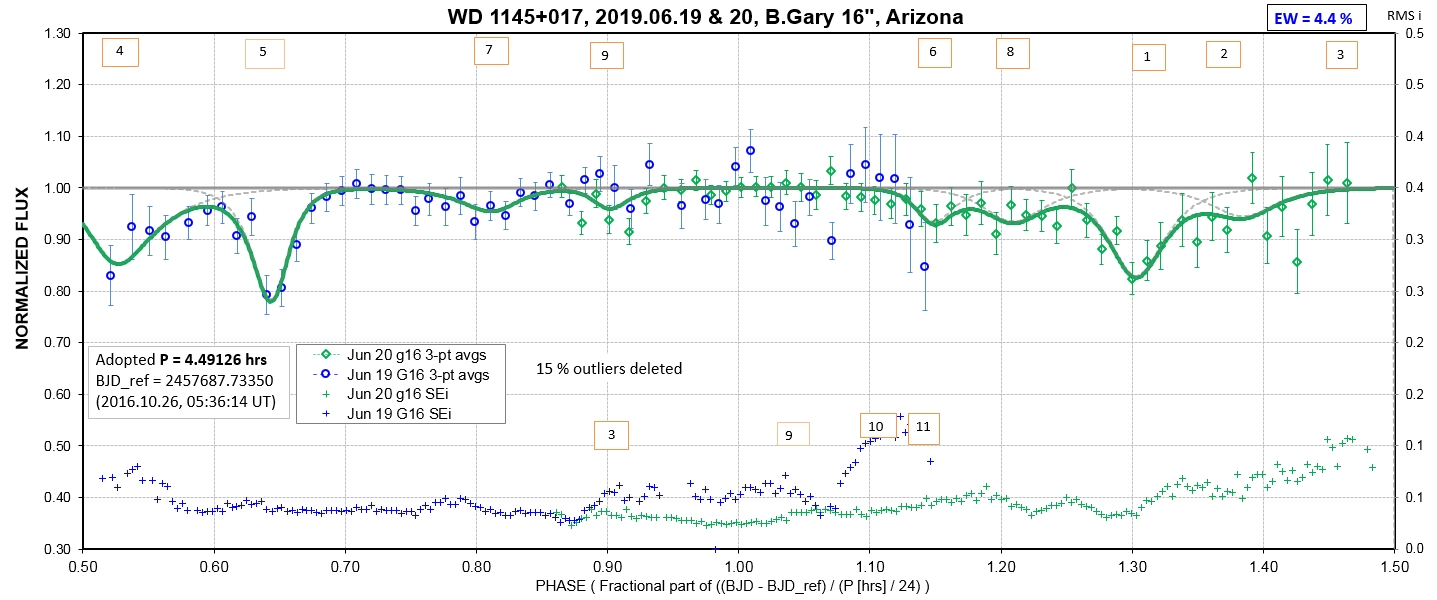
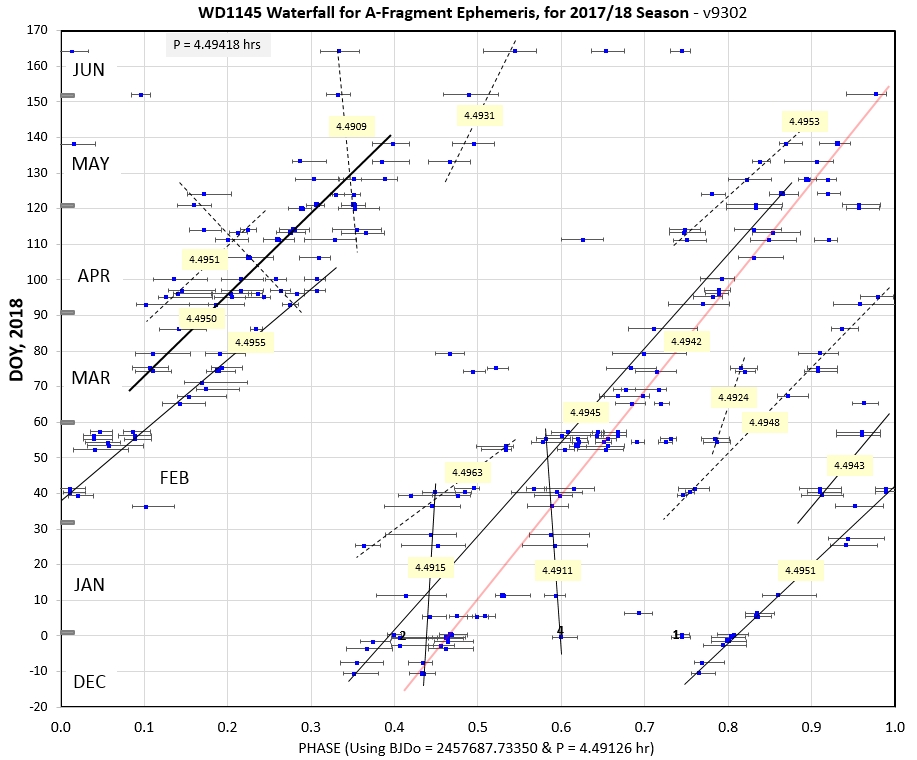
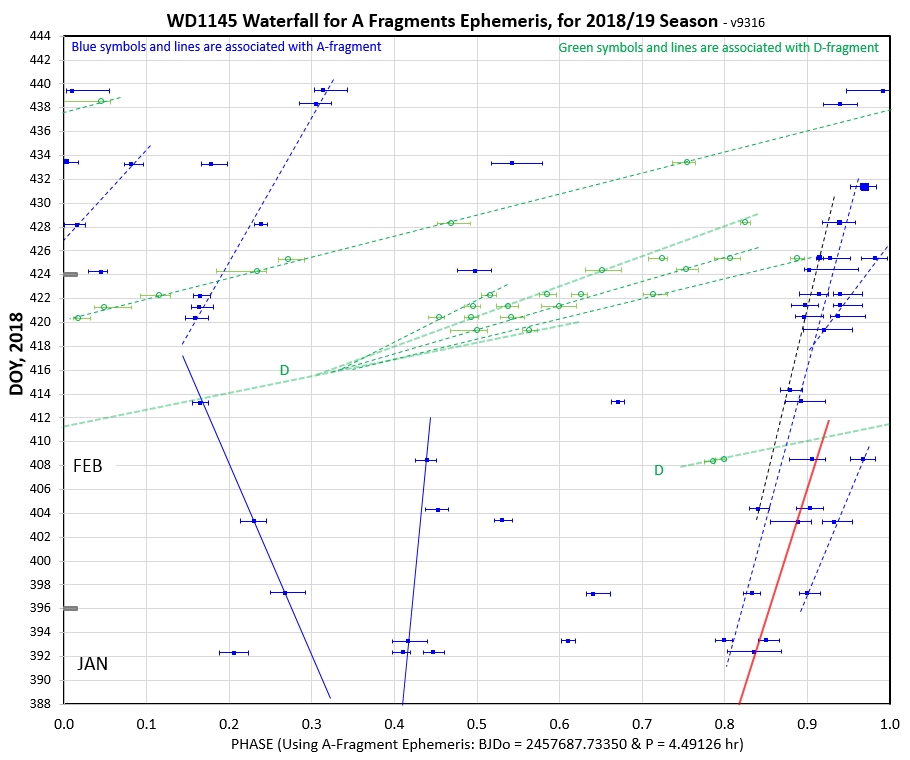
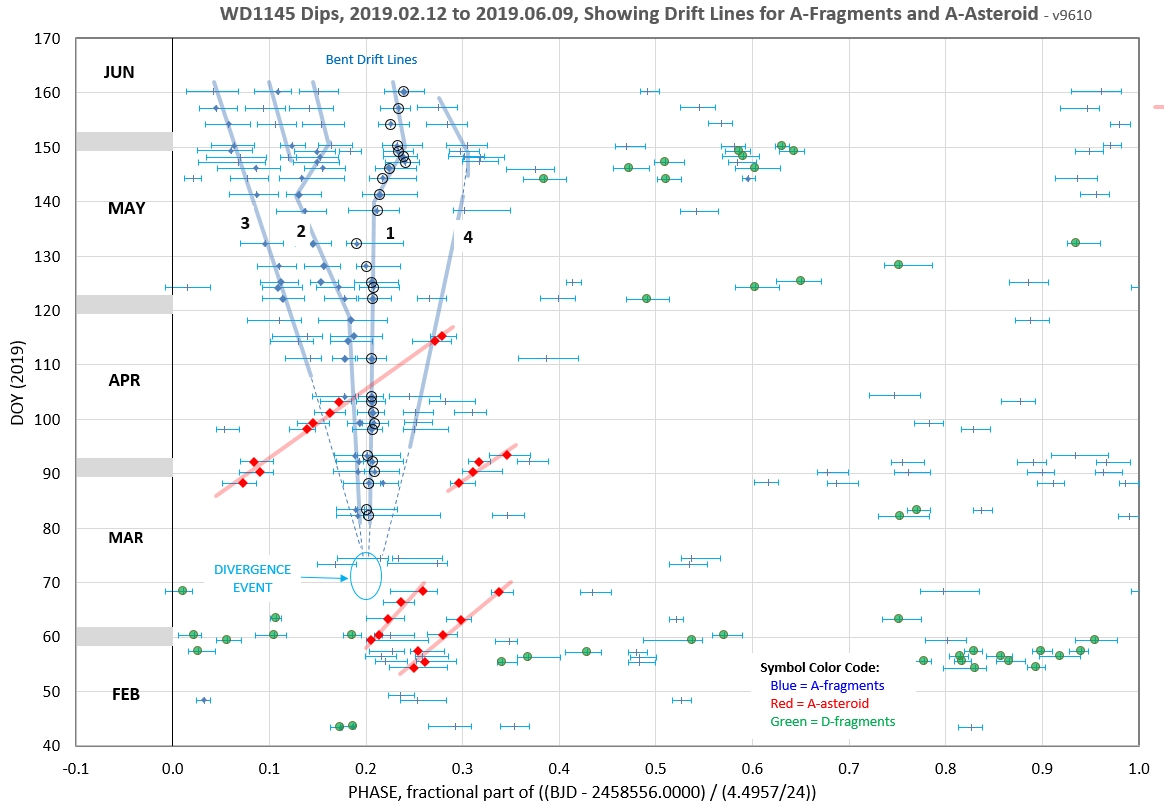
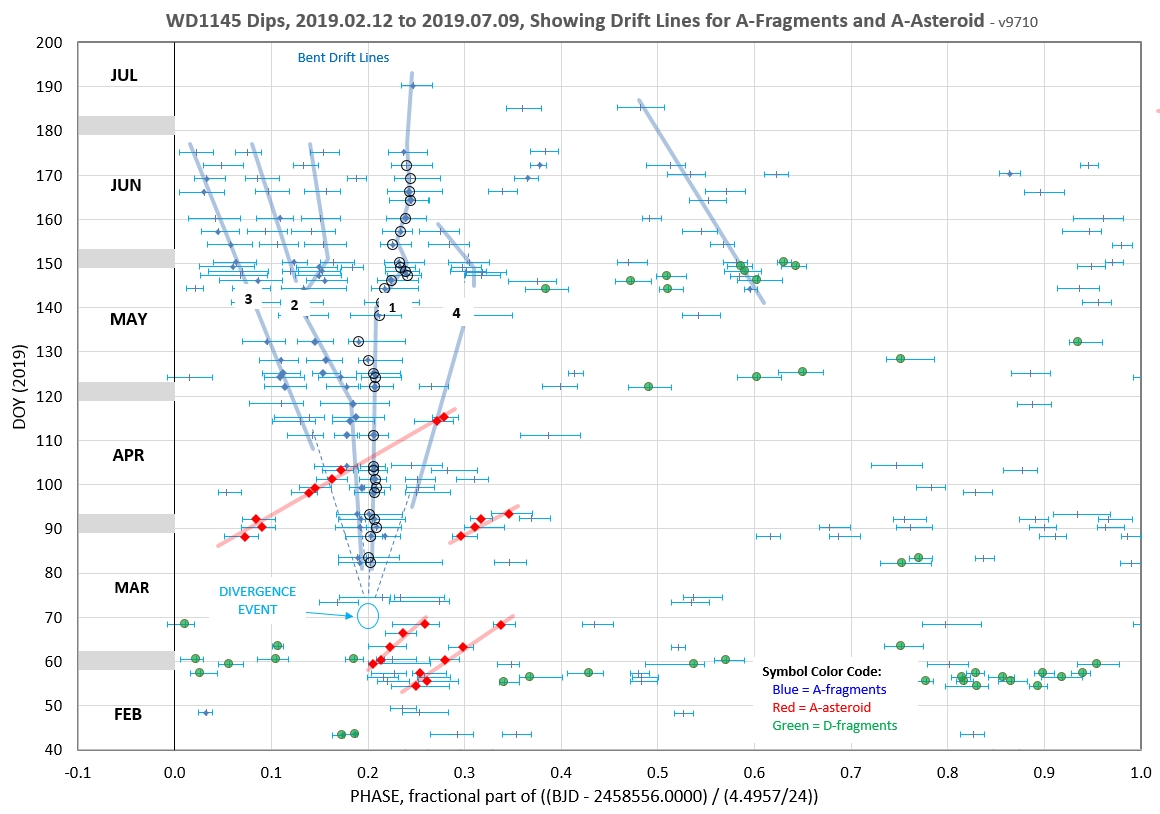
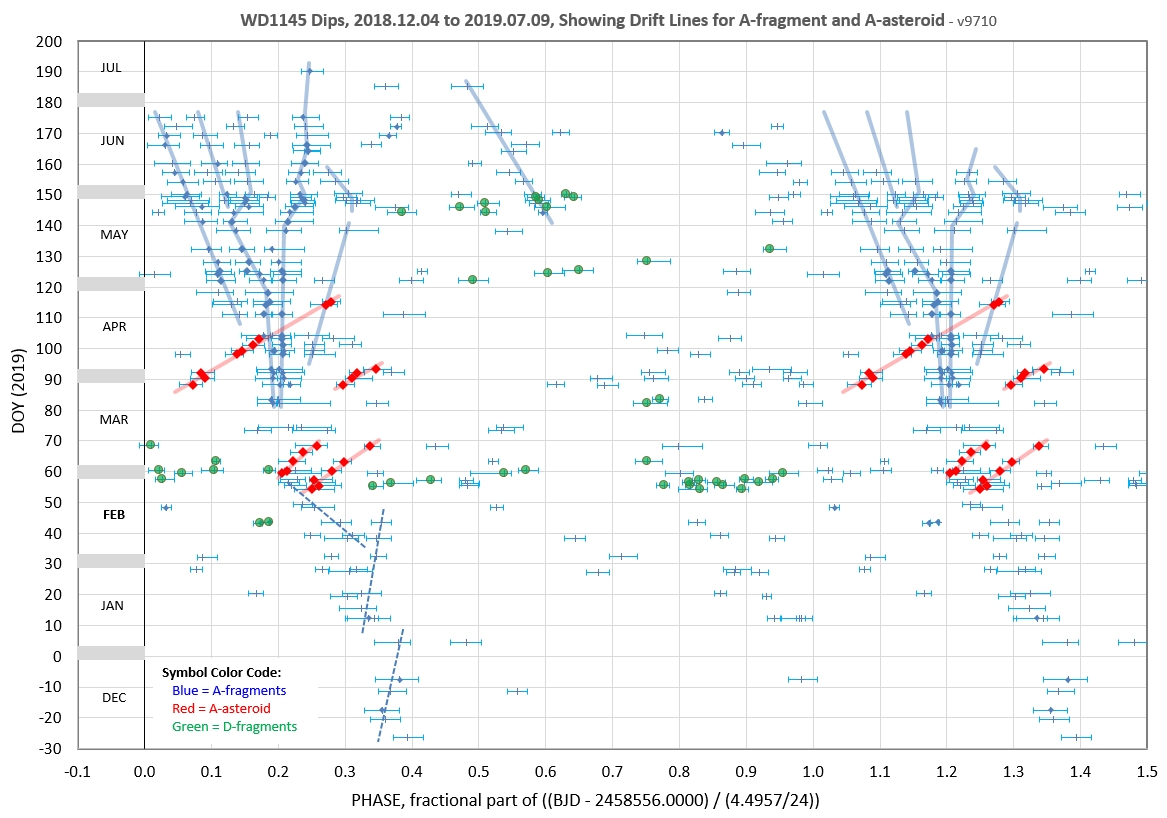
The following 3 waterfall plots show dip phase using an ephemeris for the A-fragments.









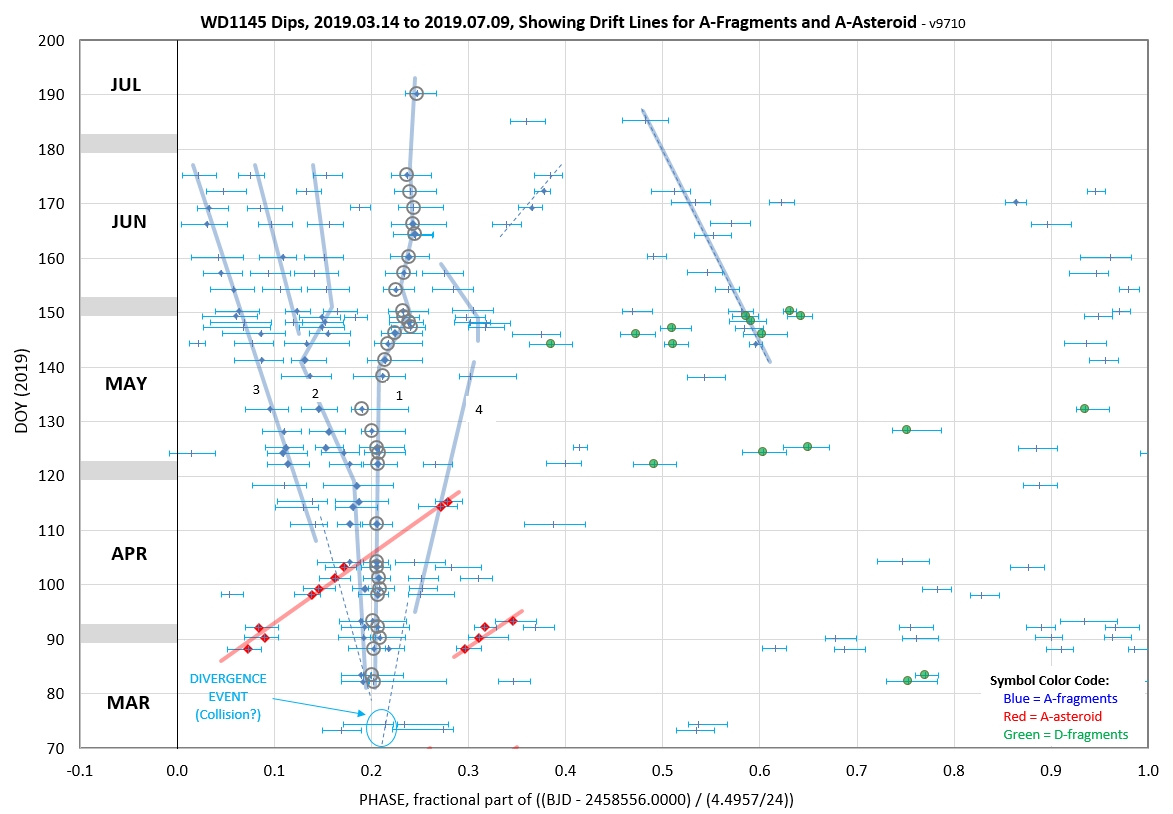
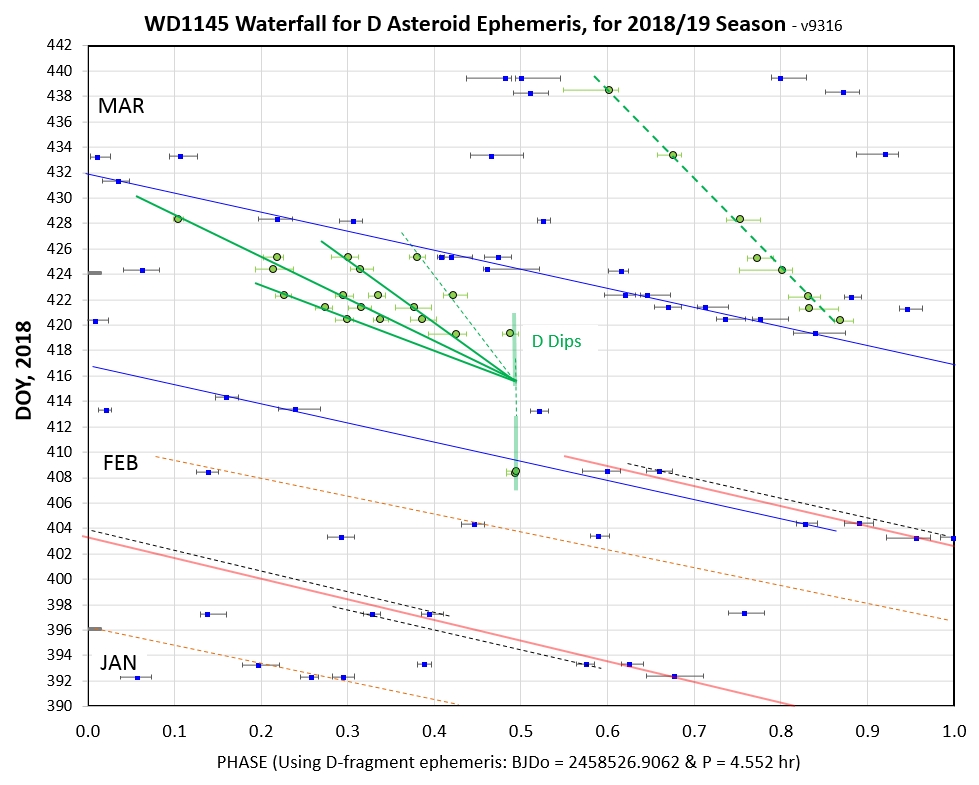
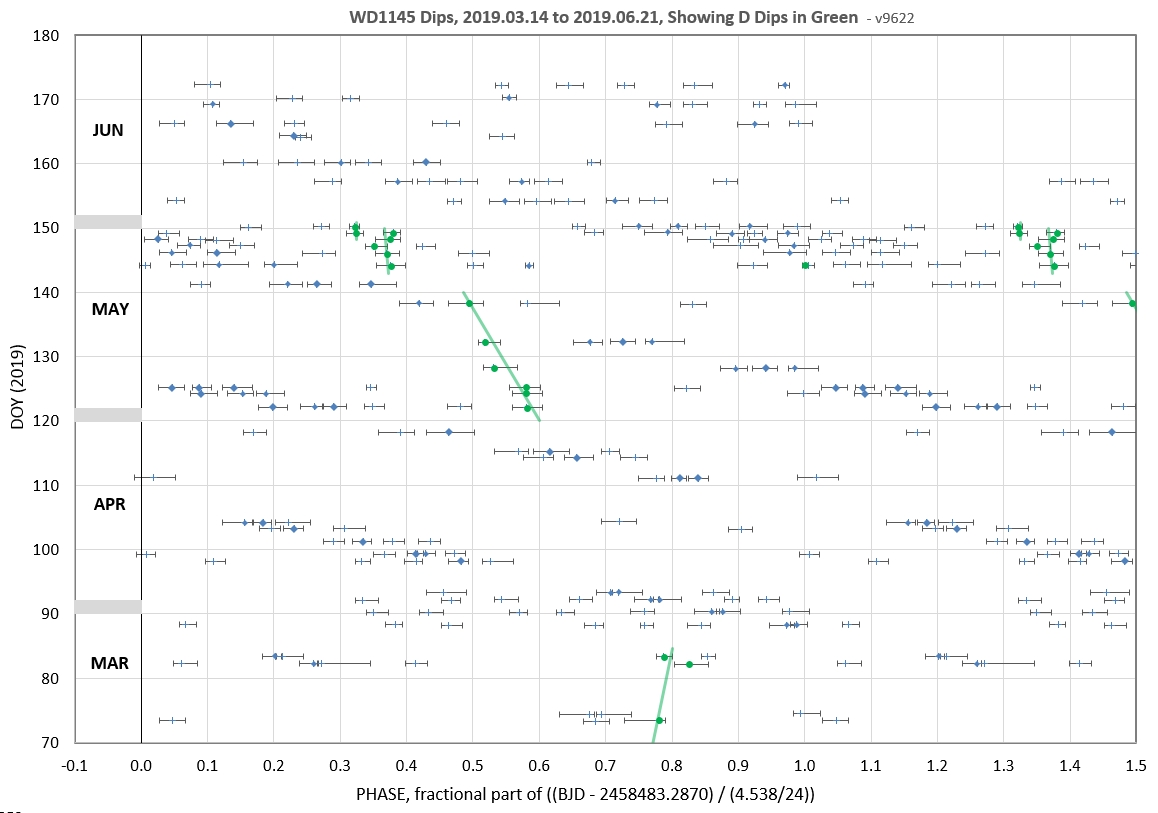
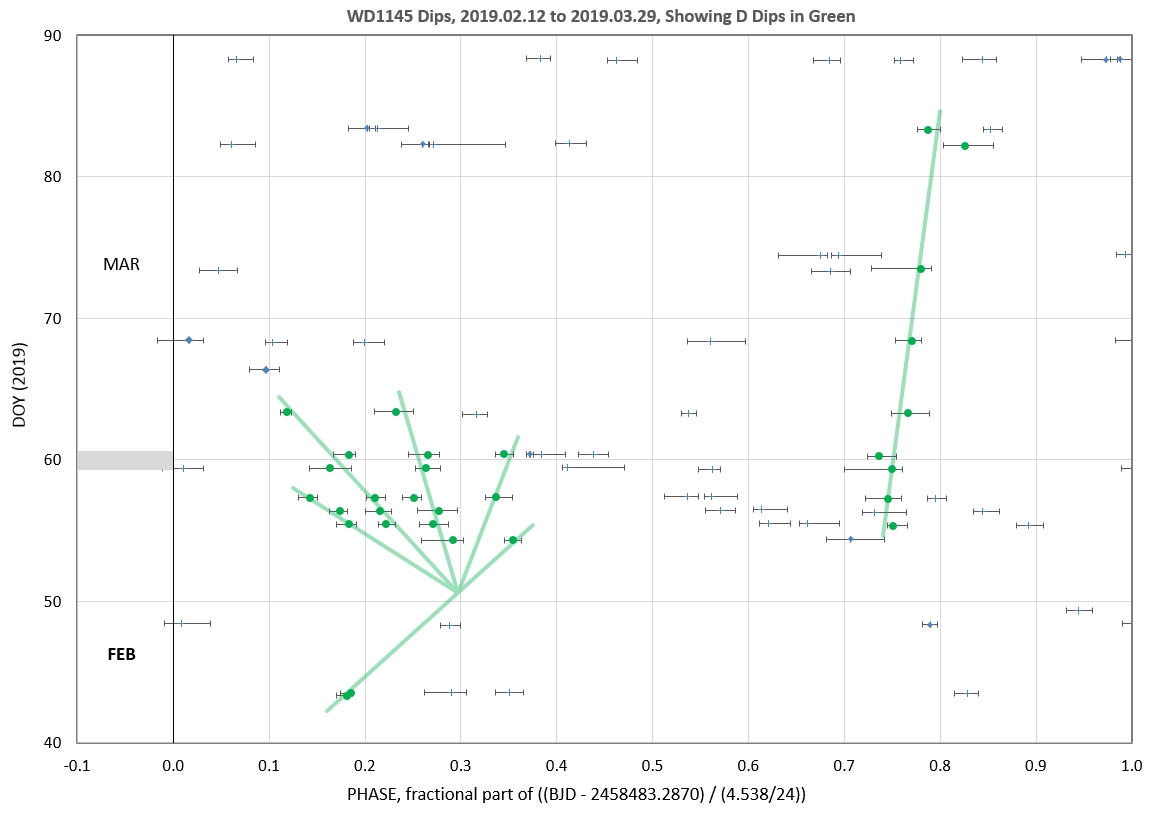
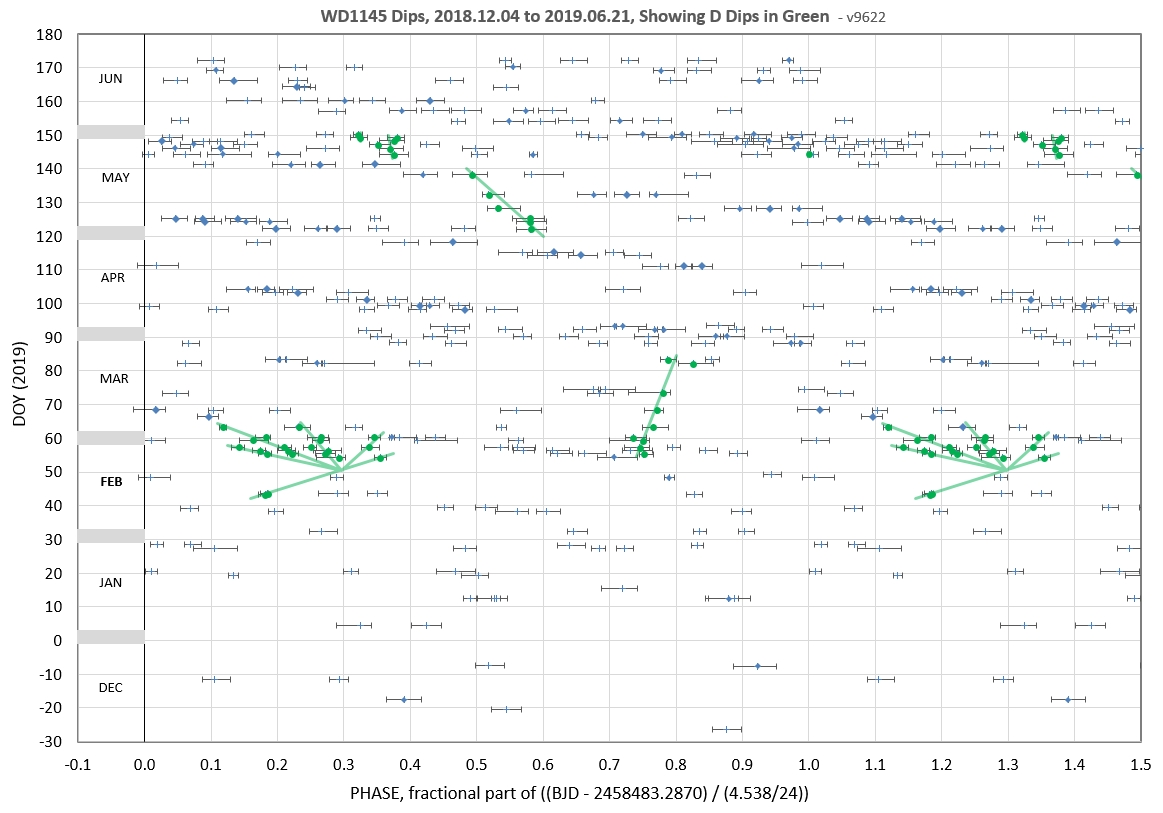
The following 3 waterfall plots show dip phase using an ephemeris for the D-fragments.







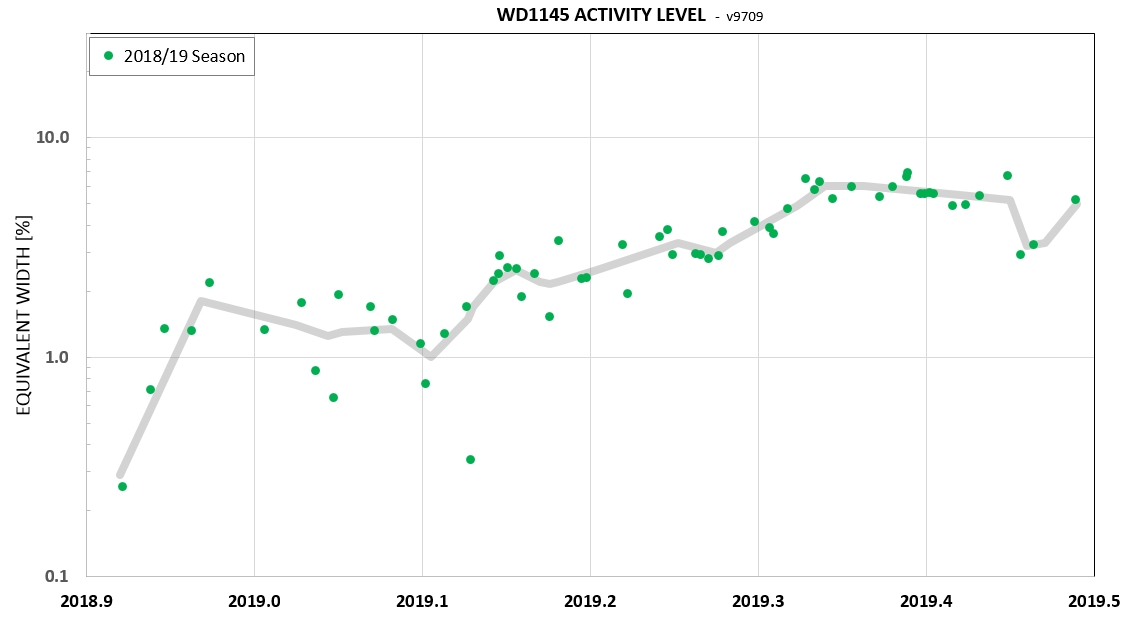
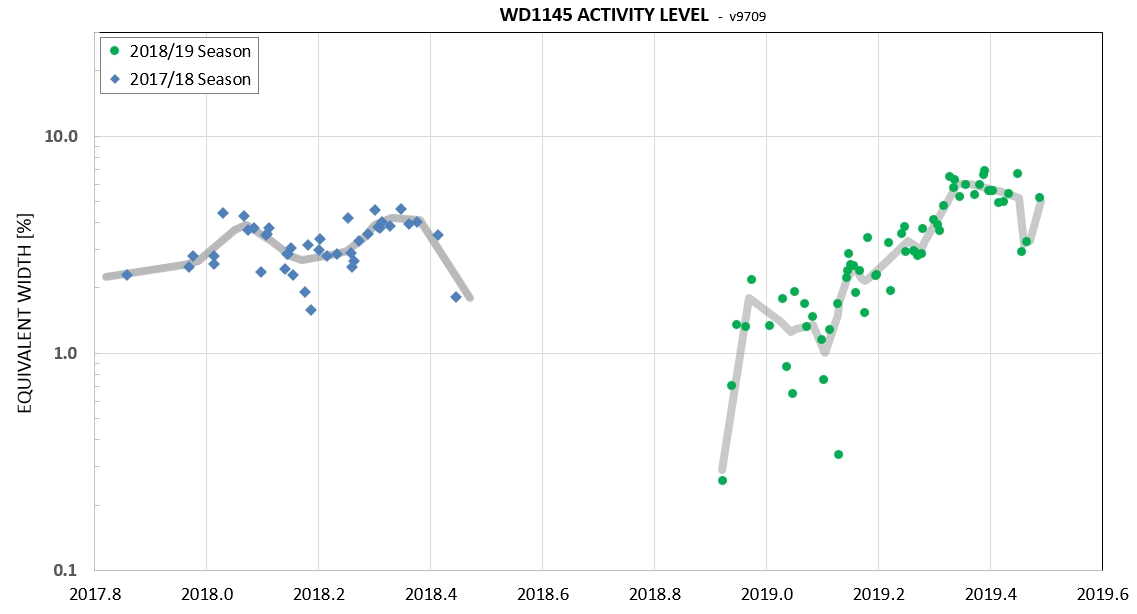
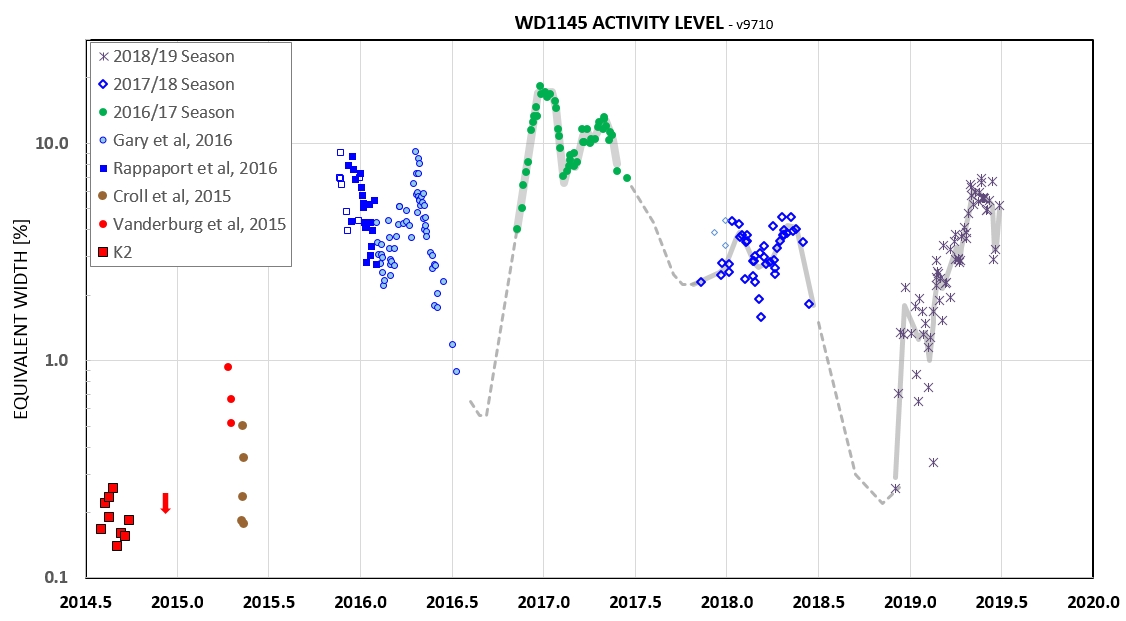
The next 3 lots show dust production "activity" level vs. date.







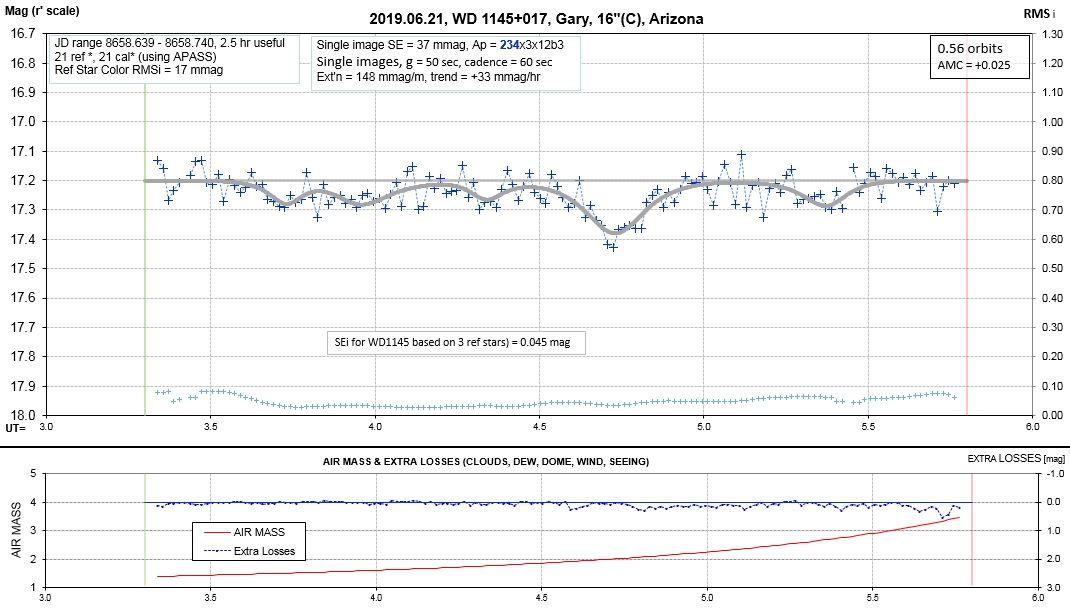
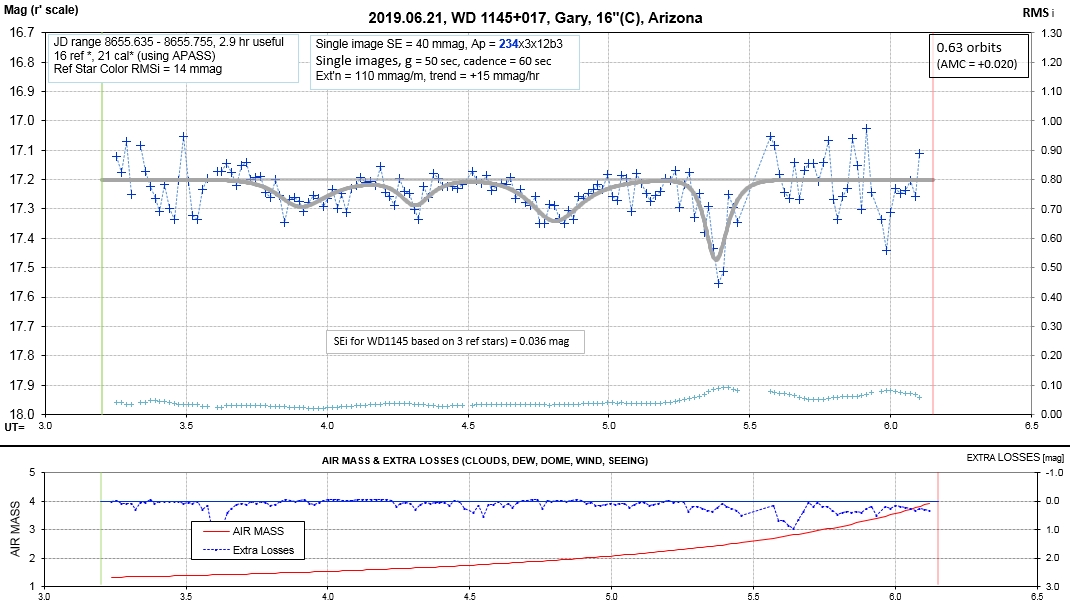
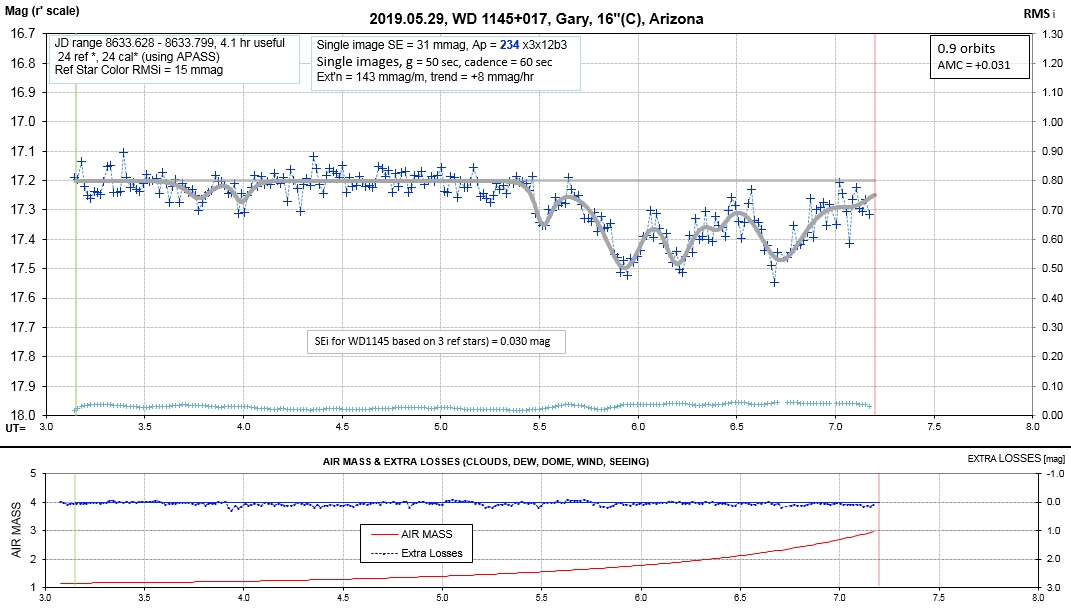
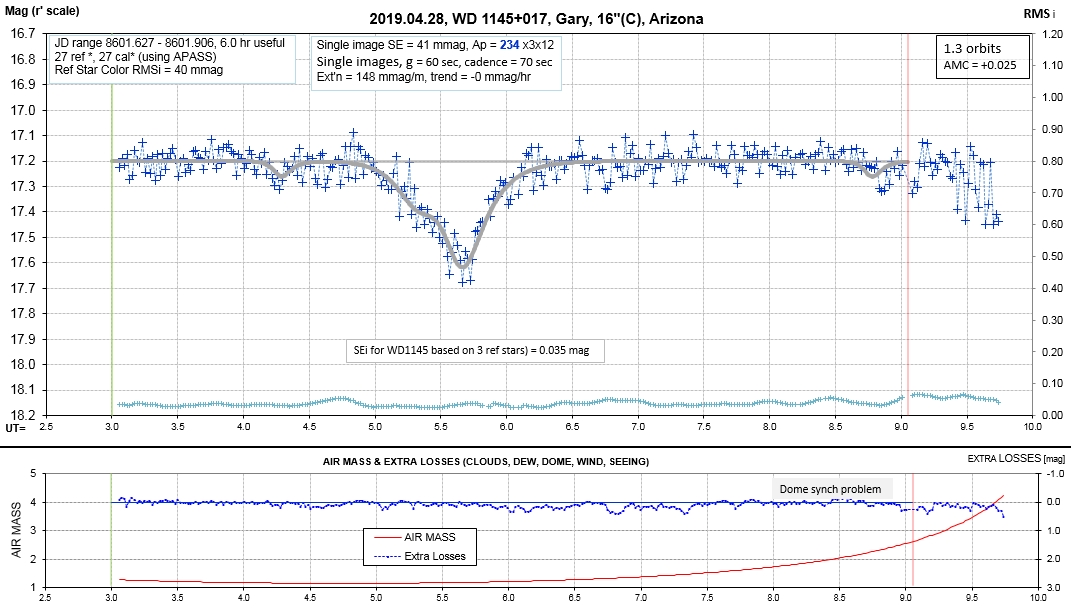
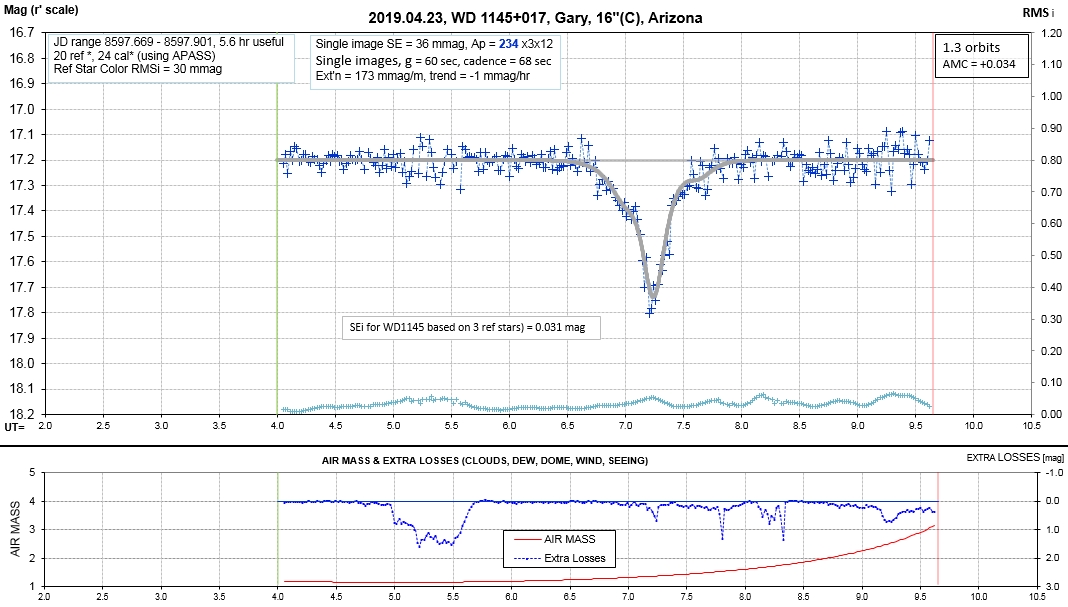
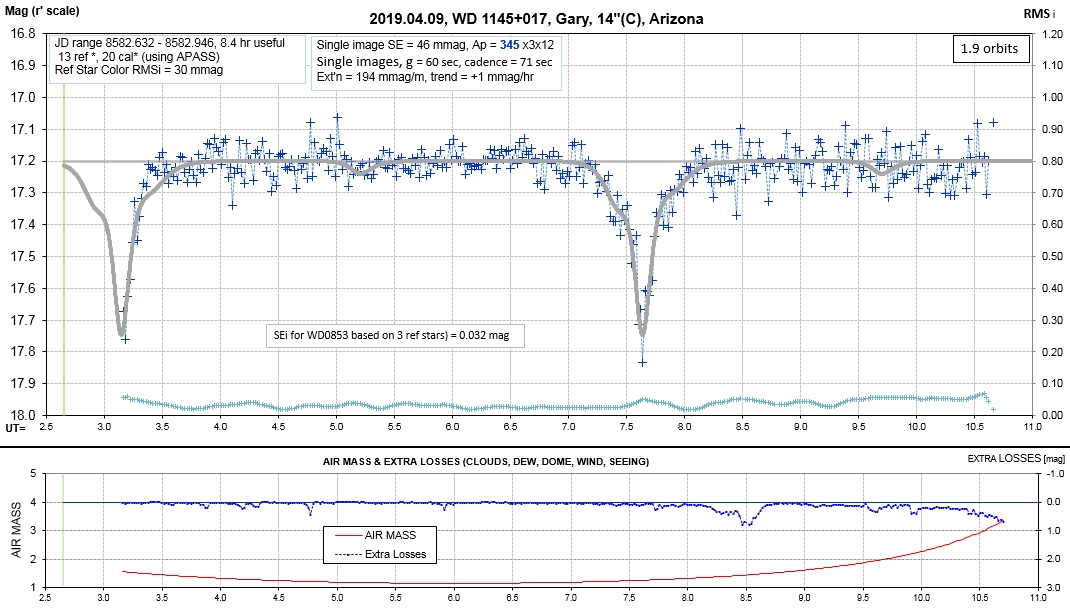
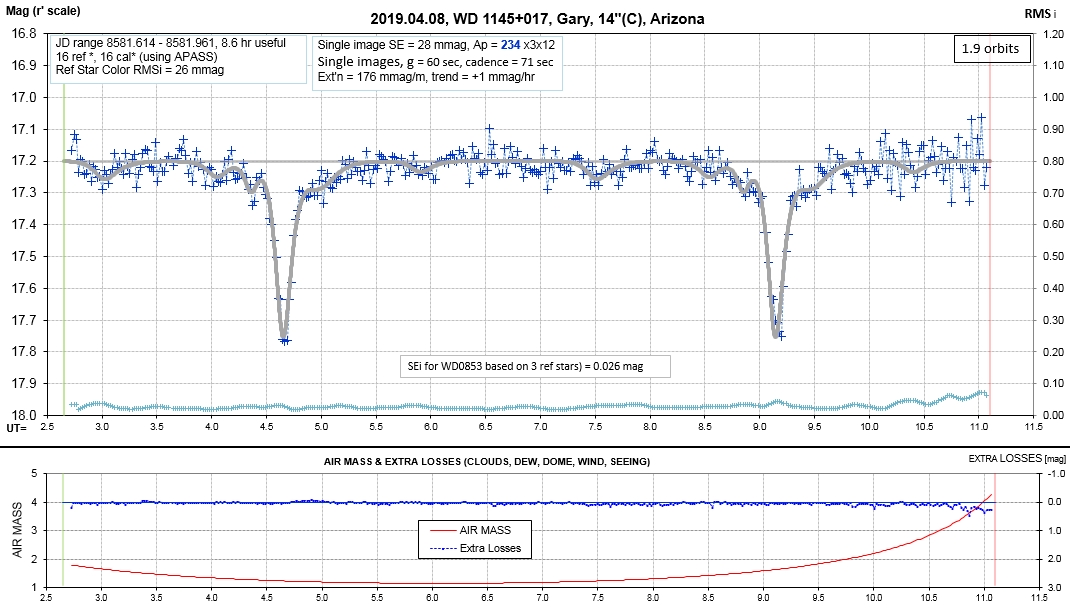
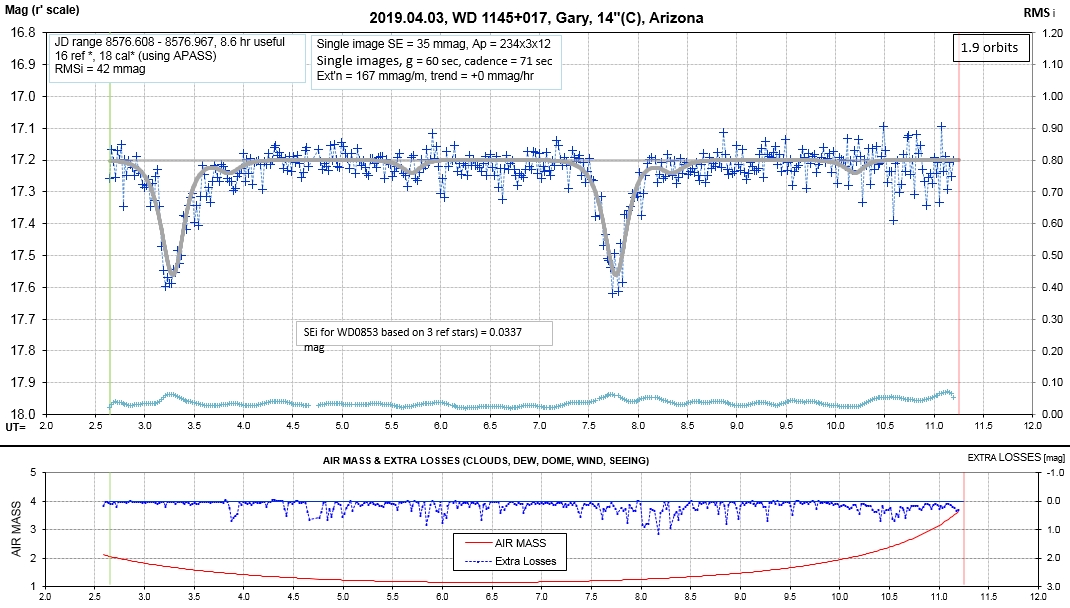
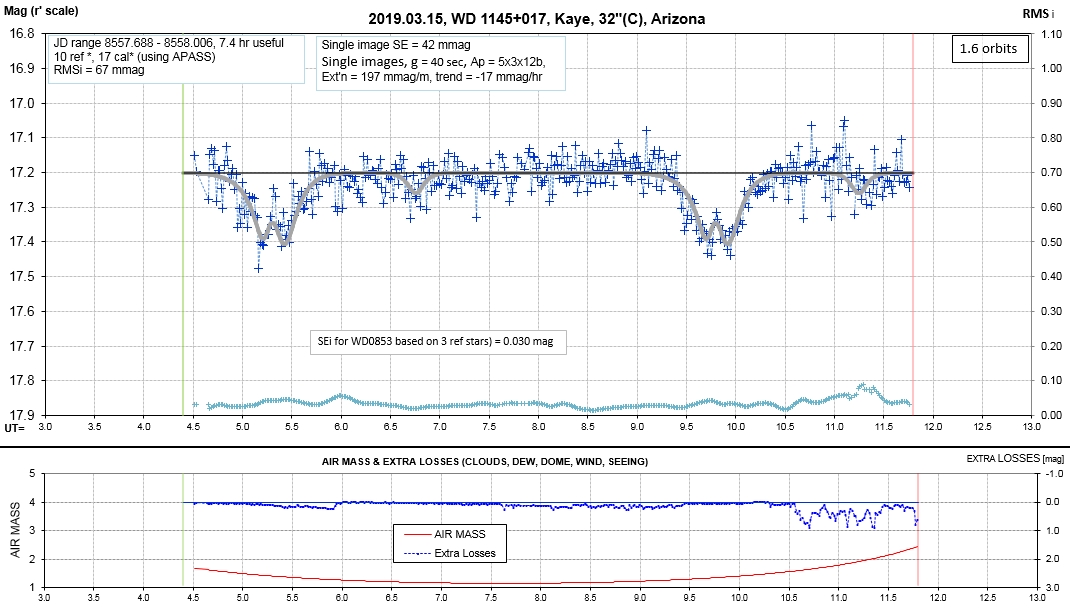
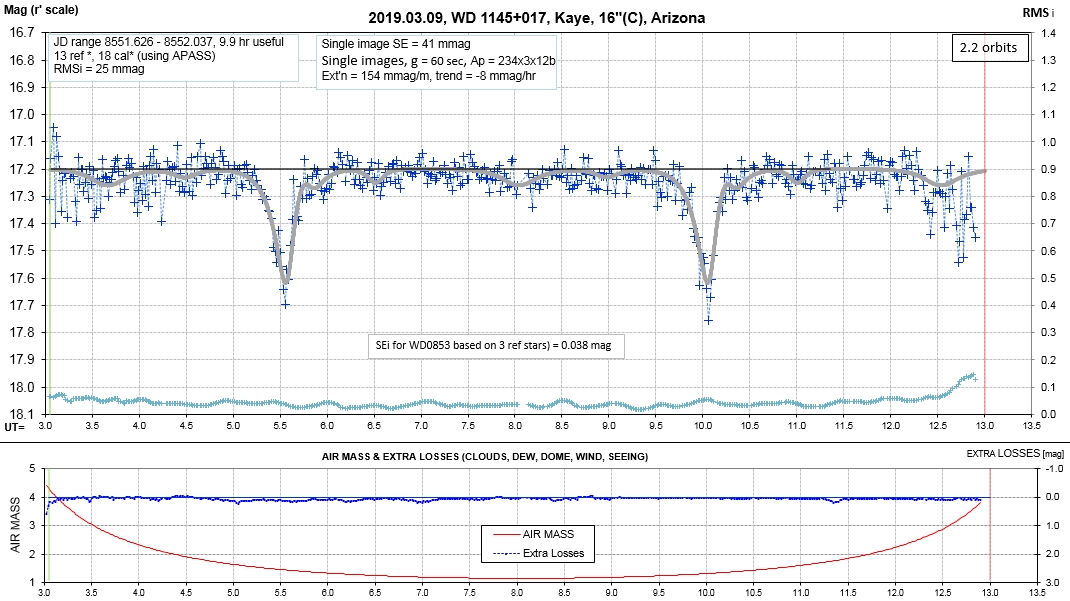
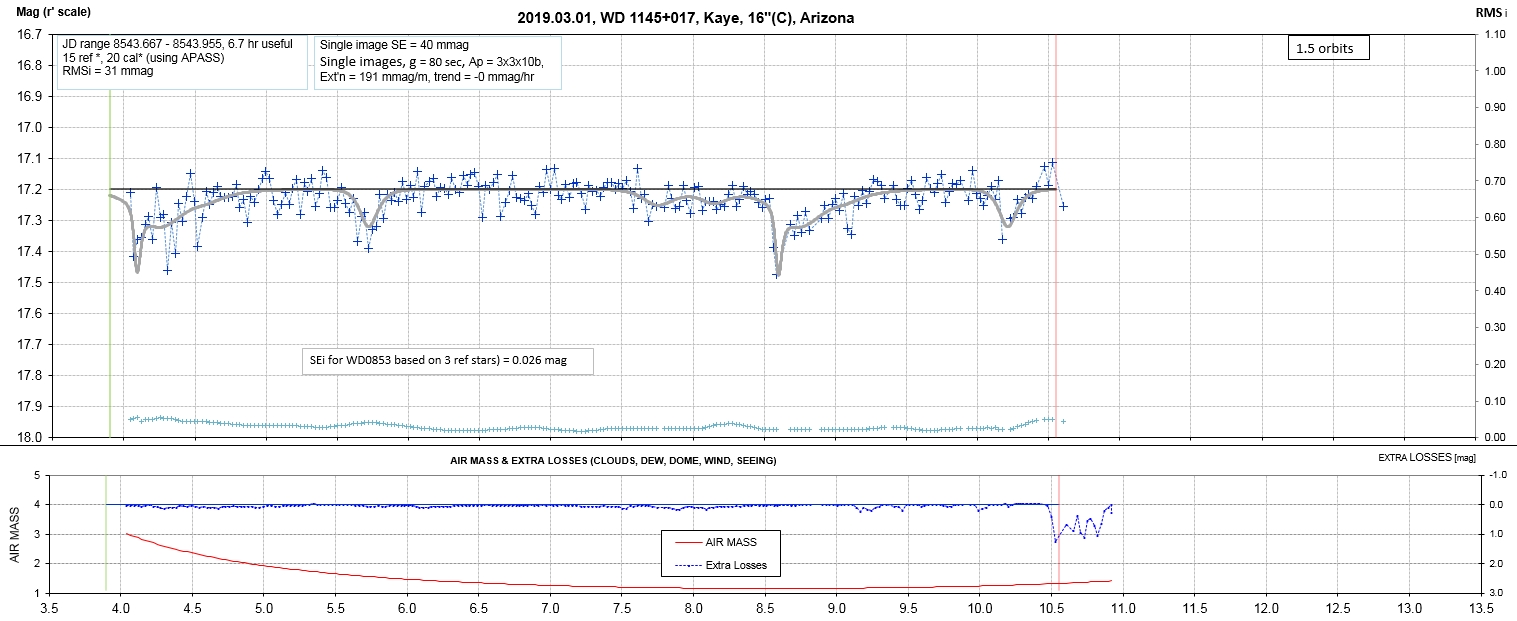
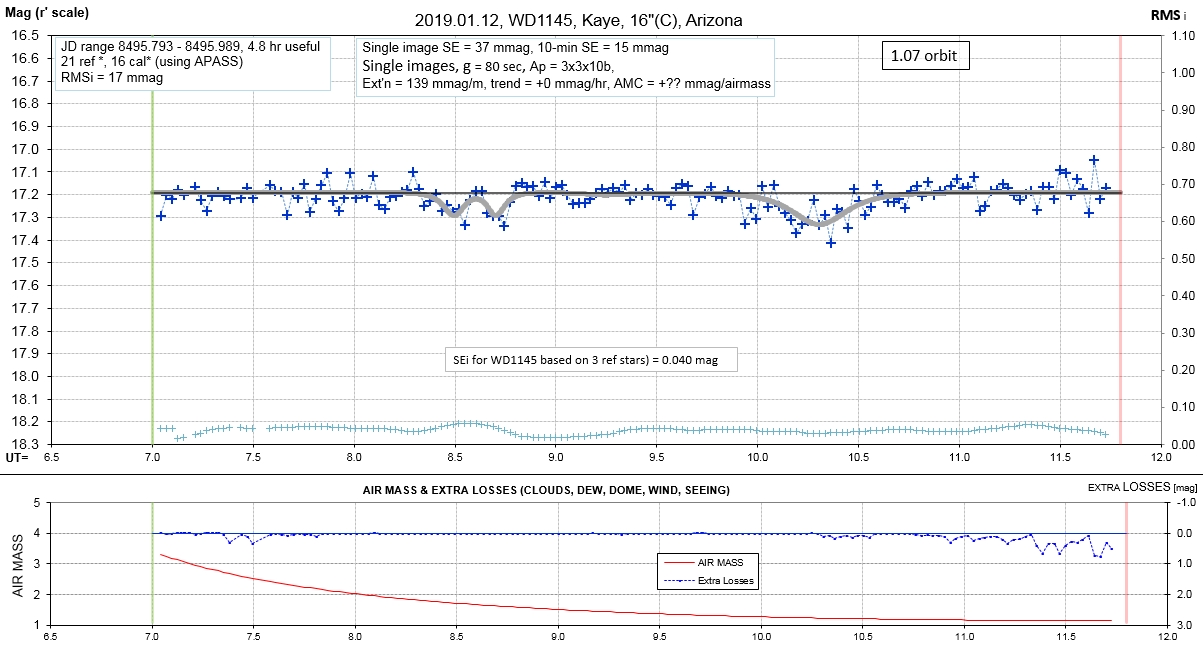
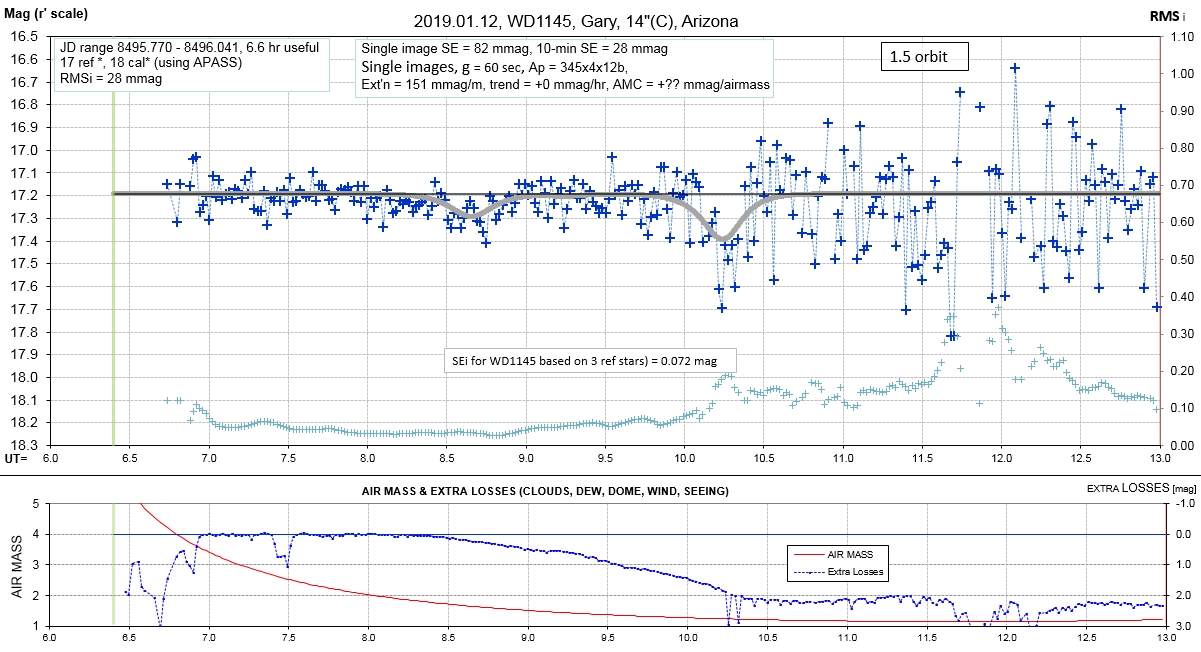
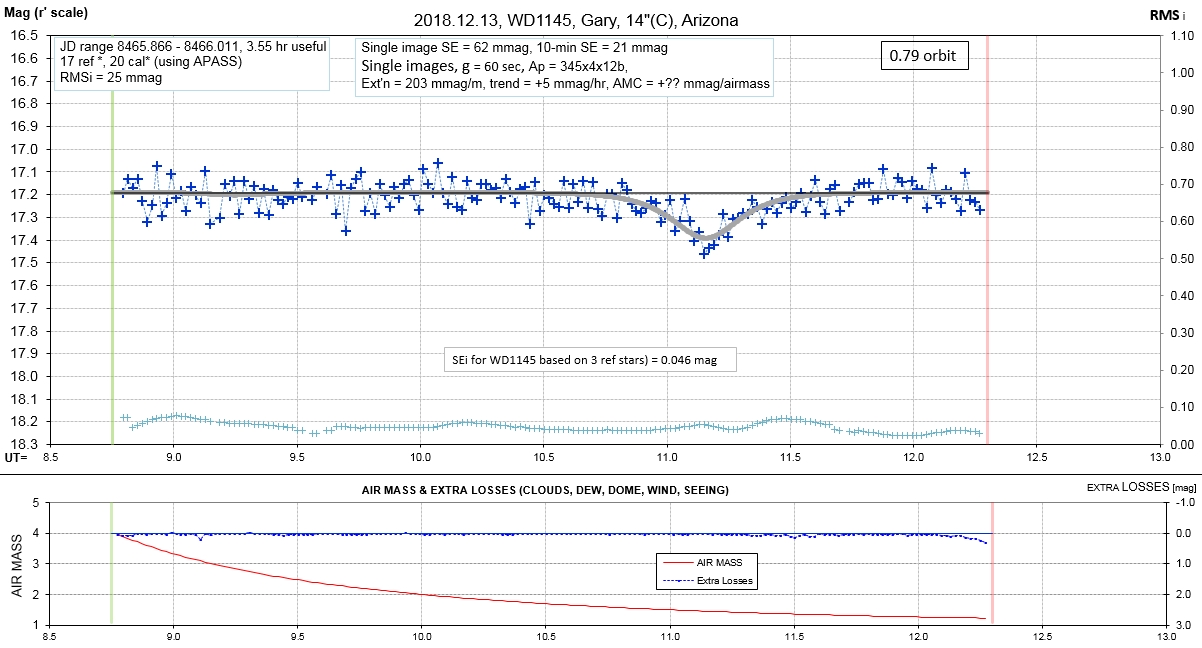
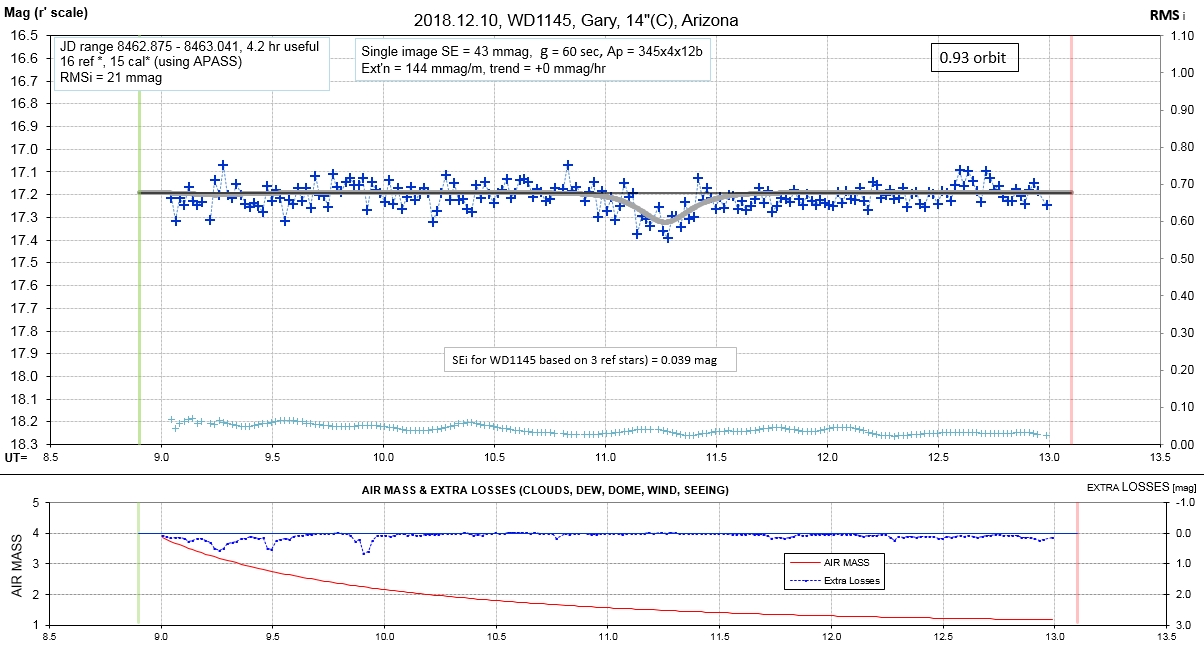
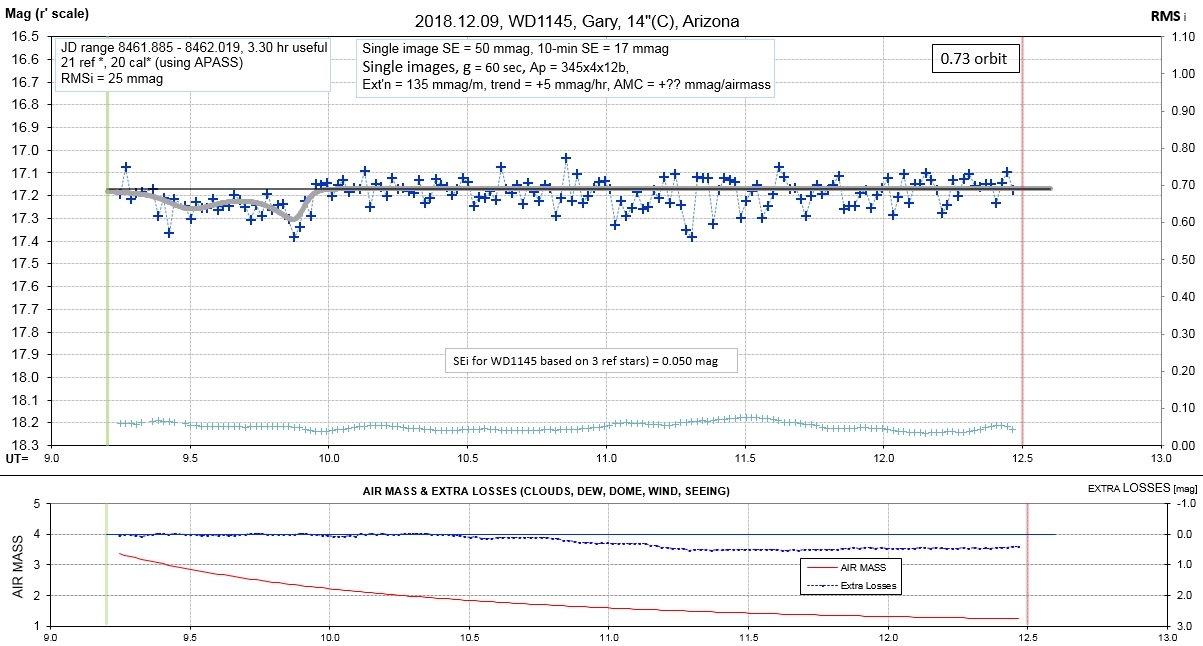
List of observing sessions   

Observing Sessions  

2019.07.09 - BG16  

Moon 13 degrees away, so noisy! Also, all high air mass.





2019.07.05 - BG16  



2019.07.04 - BG16  

Windy, so noisy.

2019.06.24 - BG16  


Dip labeled "3" is the DIp#1 in the waterfall plot for the A system.






2019.06.21 - BG16  







2019.06.20 - BG16  







2019.06.19 - BG16  







2019.06.18 - BG16  






2019.06.16 - BG16  

Poor data quality (wind), but available if desperate.

2019.06.15 - BG16  







2019.06.13 - BG16





2019.06.09 - BG16  

2019.06.06 - BG16  







2019.06.05 - BG16  





2019.05.30 - BG16  







2019.05.29 - BG16  







2019.05.28 - BG16







2019.05.27 - BG16   

2019.05.26 - TK16  

2019.05.26 - BG16  





2019.05.24 - BG16  







2019.05.21 - BG16  









2019.05.18 - BG16  

Nearby full moon increased noise level.









2019.05.12 - BG16  

Clouds before and after a short clearing provided ~ 1/2 orbit coverage. But it can be combined with data from the night before to provide ~ a full orbit of coverage.









2019.05.11 - BG16  

Clouds before and after a short clearing provided < 1 orbit coverage.



2019.05.08 - BG16  









2019.05.05 - BG16  





2019.05.04 - TK16  







2019.05.02 - BG16  









2019.04.28 - BG16     









2019.04.25 - BG16  









2019.04.24 - BG16 








Notice several events of cloud losses, as much as 1.5 mag's. 

2019.04.23 - BG16 

This is the second observation with my new telescope. It's short because I'm calibrating other properties of the hardware, but the data indicates that quality is improved over what my Meade 14" provided.





2019.04.21 - TK16 

Warm WX, and darks not at same temp as lights so cal did poor job.









2019.04.21 - BG16 

This is the first LC I made with a new telescope, an Astro-Tech 16" Ritchey-Chretien.

2019.04.13 - BG14  









2019.04.11 - BG14 









2019.04.09 - BG14  









2019.04.08 - BG14  









2019.04.03 - TK32 



2019.04.03 - TK16  











2019.04.03 - BG14  








Wind degraded several images. A few clouds were also present.

2019.04.02 - TK16 

2019.03.29 - TK32


9 % outliers removed.

 


This LC has 9 % outliers removed.







 

2019.03.29 - TK16 







2019.03.29 - BG14 







2019.03.24 - BG14









2019.03.23 - BG

Full moon was ~ 34 deg away, causing high noise level.

219.03.15 - TK32


This is an average of data from 3 telescopes.


 


219.03.15 - TG16 


After averaging in groups of 3.





2019.03.15 - BG  







2019.03.14 - BG  







2019.03.09 - TK 







2019.03.09. - BG 







2019.03.04 - TK 


Averaging groups of 5 (after sorting all observations of this date by phase).

Averaging groups of 3 (after sorting all observations of this date by phase).


No averagin (a symbol for each image). Both data sets show a brightening at phase 0.11. Could this be forward scattering from a dust cloud that doesn't block the WD disk?





2019.03.04 - BG 





2019.03.01 - TK 







2019.03.01 - BG







2019.02.28 - BG 


Dip #1 has changed shape since the day before: ingress is brief and egress is slow. One of the group of 3 D dips has disappeared (the middle one). Of these 6 dips 3 are produced by A fragment and 3 are produced by D fragments.





2019.02.26 - TK  

2019.02.26 - BG  







2019.02.25 - TK 







2019.02.24 - TK 









2019.02.24 - BG 





2019.02.23 - BG


I'm not saying the dip at phase 0.56 is the D dip, first seen on Feb 12, because it may just be a coincidence that it is located where we were looking for it. 


A gibbous moon (81 % illuminated) was 30 degrees away, which decreased SNR significantly. The first and last dips are 4.55 hours apart.

2019.02.18 - TK 




A cleaned-up version.

2019.02.18 - BG 



2019.02.17 - TK 





2019.02.17 - BG 





2019.02.16 - BG 

I was "desperate" to observe that D dip, but cloudiness ruined my observations.





2019.02.12 - TK 


Using the Kepler D period = 4.5500 hrs (and an arbitrary BJD_ref) this date's phase-folded LC for both HAO and TK16 data, shows the D dip stable in phase, at 0.79.



2019.02.12 - BG 

On this date a "sharp" dip was first seen that belongs to the D-fragment orbit. During one LC the dip appeare twice, with a separation o 4.552 +/- 0.004 hours.


This analysis shows that with an exposure time of 60 seconds, and a cadence of 71 seconds, the actual dip depth (assuming it's the same for the first and second appearance) is slightly deeper than the solution based on measurements. A source function with a deeper depth was convolved with a rectangular exposure function at appropriate exposure start times, and these results are shown by the red dash symbols. The source function has a depth of 25 % (vs. the 23 % that fits the measurements). There is negligible affect on the apparent width of the dip caused by a finite exposure time.


This is the AHS model fit when the measured values are fitted (using sum chi-squares), using one depth and shape with a UT offset for the second appearance of the dip following the first appearance by 4.552 hours (also solved-for). 

 

Using the Kepler D period = 4.5500 hrs (and an arbitrary BJD_ref) this date's phase-folded LC for HAO data shows the D dip stable in phase, at 0.79. (I later refined the D dips period to be 4.552 hrs.)


Phase folding with the A-fragment period shows the main dips at different phases.


The more accurate separation of the two main dips is 4.552 +/- 0.004 hours.


This is the LC that forced me to recognize that a D dip was present, and it was "sharp" (like most dips at "turn-on").

2019.02.07 - TK  





2019.02.07 - BG 





2019.02.02 - TK 





2019.01.28 - TK 





2019.01.27 - TK





2019.01.27 - BG





2019.01.20 - TK 





2019.01.19 - TK 





2019.01.19 - BG 



2019.01.17 - TK 




This was a short test observation meant for checking master calibration files, but it's somewhat useful for excluding presence of dips.

2019.01.15 - TK 




We are puzzled about the main dip being shallower in this (TK) data than BG data.

2019.01.15 - BG 


Note: There is no evidence of the "double-dip" feature that was present on Jan 12.

2019.01.12 - TK 




First observations with TK's new 15" telescope. No calibration (dark or flat).

2019.01.12 - BG  


Dew formed on my front corrector plate, starting (probably) ~ 9 UT.

2019.01.04  





2018.12.19 





2018.12.13





2018.12.10  




This dip is credible.

2018.12.09 


I'm skeptical about the two dips at the beginning.

2018.12.04



2018.11.27


 

2018.11.16



2018.11.09 


This is the first observation of the season.

± 520 K (Izquierdo et al., 2018)
A asteroid radius and mass = ~ 200 km and 1/10 Ceres, i.e., ~ 10²⁰ kg (Rappaport et al., 2016)
Kepler-based transit periodicities (A - F) = 4.49 to 4.86 hours, (Vanderburg et al., 2015)
Asteroid orbital speed (A - F) = 319 to 311 km/s
A asteroid time to cross WD diameter = 53 seconds (for central crossing)
A asteroid transit depth ~ 0.56 mmag (assuming 200 km radius)


WD1145 (blue circle) is at 11:48:33.59 +01:28:59.3 (J2000). Red-circled stars have stability suitable for use as reference. FOV = 27 x 18 'arc, northeast at upper left.

Miscellaneous Analyses and Speculations

So far ground-based observations have detected dust clouds with orbits associated with the K2 measurements of the A, D and B periods, as shown below. 


Figure M01. Scatter plot for some of the drift lins of the past few years, converted to average orbit radius. 



Figure M02. Same data for just the inner-most three orbits. The WD radius ~ 8400 km, so the A dust clouds are typically ~ 700 km closer to the WD than their parent asteroid.


Figure M03. Diagram, to scale, of the Kepler A, D and B orbits, looking "down" from a "pole", including the 2015/16 dips associated with the Kepler A period, located at random orbit asimuths but at their true orbit distances. The shape, labeled "Most common dip size," corresponds to a dip size that produces a dip depth of 30 % (which was comon for that season). Since particles ejected with velocity components for and aft are orbitally sheared to greater and smaller azimuth values they define an oval shape that would keep expanding if those particles didn't sublimate out of existence.   

The above two graphs are based on plots like the following:


Figure M04. Waterfall plot for the 2017/18 observing season, using the A ephemeris (as described in Rappaport, 2018).

Figure M05. Waterfall plot for the current observing season, using the A ephemeris (as described in Rappaport, 2018).

Figure M06. Waterfall plot for the current observing season, using the D ephemeris (described below)

This waterfall plot has evidence for the creation of several fragments of the D asteroid on DOY 416 (2019 Feb 19).

The use of P = 4.552 hours is required by the 2019 Feb 12 light curve, below.


Figure M06. This standard light curve shows two "sharp" dips with identical shapes that are separated by 4.552 +/- 0.004 hours, which corresponds to the K2 D period (4.550 hours).



Figure M07. Detail of the first and second appearance of a dip with identical structure on 2019 Feb 12 (shown in previous figure) separated by 4.552 +/- 0.004 hours. The times of image exposures is shown by the x-location of the red bars, and the average of a hypothetical source function normalized flux during these exposure times is shown by the red bar y-locations. The source function was adjusted to achieve agreement with the observations. 

This detail of the two dips shows that the 60-sec exposure times had only a slight effect on inferred depth of the "source function" (what would have been observed with short exposures). The source function has a depth of 25 %. How can a dust cloud that covers 25 % of the WD disk cross in only 2.5 minutes, considering that a point source crosses the disk in only 0.9 minutes? This deserves an analysis of the geometry of cloud size and crossing time.

Speculation:

Let's tell a story describing what may have happened in the D orbit last week.

Repeat of Fig. M05.

In the above figure let's imagine that the D asteroid has a large crater that has reached a surface temperature of ~ 1900 K. Near surface sublimation occurred and produced a small dust cloud at DOY 408. Since its source is the asteroid it will have a center of activity fixed to the asteroid period, not a period associated with an orbit at the asteroid's front surface. The asteroid's front surface may be 100 km closer to the WD than the asteroid center, This is indicated by the first vertical green bar.

This activity subsided by DOY 413, shich accounts for a gap between the vertical green bars. A subsurface heat wave reaches lower levels that exceed the temperature of a layer with volatile mineral, causing the formation of a gas chamber with pressures that eventually exceed the strength of overlying material. An explosive ejection of four fragments occurs on DOY 416. Since it was a crater on the star-facing surface that was the source of the explosive ejection the ejected fragments will be in elliptic orbits with a smaller average orbit radius than the parent asteroid. None of the ejection velocity is lost by overcoming the asteroid's gravity because the WD gravity field matches the asteroid's gravity (in a rotating reference frame). This is equivalent to stating that the Hill sphere radius (same as Roche lobe) equals the asteroid radius. In theory, a rock on the surface could "float away" with the smallest nudge.

After 4 or 5 days these fragments became active sublimators on their fresh surfaces, producing the 3 or 4 drift lines sloping off to the left.

COLLISION MODEL

The paper by Su, Jackson & 15 others (download) presents a model that can account for observed variations of near-IR thermal emission of a young star's debris disk. The model is based on collisions that produce dust clouds with finite lifetimes, and I think it has possible use in explaining WD1145 transit fades. Although the paper's purpose is to account for IR thermal emission from the debris disk the same dust cloud model could be used to explain transit dips of the star by such a disk if it was inclined edge-on.

The WD1145 discovery paper (Vanderburg et al, 2015) suggested that the transiting dust clouds are produced by the sublimation of minerals on the surface of planetesimals (in the 5 Kepler orbits). Presumably, a mineral molecule would sublimate from the surface and combine with others to form a particle, and this particle would continue to move away from the surface to join other such particles and form a cloud. I personally preferred a model in which a heat wave penetrated to a depth where a volatile mineral was present, and when it sublimated the gas pressure build-up until it overcame structural forces of overlying material and explosively created a jet that ejected the overlying particles. (From my moon work, 5 decades ago, I knew that depressions were warmer than a surrounding flat surface, and these depressions were favored sites for the creation of "sublimation jets." Observations by the Rosetta spacecraft, orbiting Comet 67P, found dramatic evidence for this with deep pits being the source for ejected material.) Ever since this model was under consideration there has been no credible mechanism to account for the large ejection velocities required for the particles in such clouds. Note that this model assumes quasi-continuous production of dust due to either surface sublimation or sublimation jets that eject overlying dust. Whereas the discovery paper assumed the source of these dust ejections was a planetesimal (on of the 5 associated with periods A through F), later thinking favored dust coming from a source of many fragments that drift away from the planetesimal (due to Hill sphere shrinking to the planetesimal's surface). Each dust particle would have an ejection location that its new orbit would pass through. Although it is likely that particles are ejected isotropically, with a range of speeds, it will be useful to focus attention of the following 3 velocity components: up/down, in/out and fore/aft.

Particles ejected

inclined so that they extend to the + and - 0.50 WD radius locations. For particles to reach those heights above the source fragment's orbit plane they would have to be ejected with a speed of 2 km/s (as derived below). So far no one has made a case for sublimation jets being able to achieve these speeds.

Collisions, on the other hand, can achieve speeds of these amounts [need a reference for this]. Whether a particle is ejected by a sublimation jet or a collision, it will be subject to the same celestial mechanics described above. A particle ejected from a collision will have the same behaviors associated with the up/down, in/out and fore/aft categories. The up/down and in/out particles would be in orbits that return them to the collision location, and anti-collision location, every orbit. The fore/aft particles would initially join the other particles for these convergences, but over time they would spread out along the orbit. In other words, the dust cloud would expand and contract twice per orbit! Before Keplerian shear produces significant spreading out along the orbit it can be said that all particles will fly apart and come back together "in phase" - producing a dust cloud expands and contracts twice per orbit.

Note, however, that since the Earth's line-of-sight to the WD is for just one orbit location we will observe the dust cloud when it is at the same phase of its expansion/contraction cycle. It will therefore produce the same dip depth for every passage in front of the WD. None of our observations will reveal dust cloud changes in size between transit events.

The interesting bonus for the collision model is that every time the dust cloud contracts, the dust and any larger fragments of the source fragment will pass each other at close range with large relative velocities (on the order of 1 to 8 km/s). Ever contraction therefore affords a new opportunity for additional collisions! An initial collision may start a cascade of subsequent collisions. This could be a source for replenishing the dust cloud with new particles. 

The cascade of subsequent collisions every half orbit could replenish particles that sublimate out of existence during the time it takes for them to spread along the orbit (due to "Keplerian shear"). We don't know the timescale for particles to sublimate out of existence, but if we knew the function for particle ejection speed vs. particle size we could use the observations of dip width to model the sublimation parameters. For example, here's an observation of a dip that has a stable width of ~ 0.04 phase units (11 minutes):

Figure M10. Waterfall plot showing a set of drift lines (DLs) that diverge from a specific phase location at DOY ~ 71 and phase = 0.2. This DOY is presumably the date of an initial collision that created four clouds of dust and chunks of material that may have continued to collide every half orbit for the continued production of new particles and smaller chunks. Properties for DL#1 are shown in the previous figure.

Before DOY ~ 71 there was no evidence for the dust cloud under consideration, which is additional evidence that it was created by a collision on the DOY and phase associated with the DL divergence location.

Note that for the original mechanism suggested for the production of the dust clouds, sublimation jets, the dust cloud would remain the same size throughout its orbit even though the particles are constantly moving throughout the cloud (the only exception being a continual spreading out along the orbit due to Keplerian shear). For the collision model, however, particles and fragments created by a collision will be in clouds that are expanding and contracting twice per orbit, with coming together events occurring twice per orbit, for possible subsequent collisions and the creation of new particles.

Ejection Speed Requirement

What ejection speeds are required to account for the light curve observations? The deepest dips are ~ 60 %. We don't know the optical depth of the dust clouds, so consider the two extremes of totally opaque and semi-transparent. A totally opaque dust cloud that covers 60 % of the WD disk would produce the deepest dip recorded. The next figure shows how much of a disk is covered by an opaque band-shaped object with one edge intersecting disk center and the other edge located at a fraction of a radius toward a pole. For example, an opaque cloud shaped like a band (with edges aligned with the orbit) that extends from the equator to a latitude of 30 degrees will obscure 60 % of a hemisphere.

Data Exchange Files   

    2015.11.21 to 2016.07.15  
    2016.10.25 to 2017.06.18  
    2017.11.10 to 2018.06.18 
    2018.11.09 to 2019.06.09 

Related Links  
    Mukremin Kilic's pro/am search of dusty WDs for dips:  https://www.nhn.ou.edu/%7Ekilic/Docs/dusty.html
    Some observing "good practices" for amateurs (book): Exoplanet Observing for Amateurs
    Hereford Arizona Observatory (HAO):  http://www.brucegary.net/HAO/
    Tutorial for faint object observing techniques using amateur hardware: http://brucegary.net/asteroids/  
    Master list of my web pages & Resume

WebMaster:   Nothing on this web page is copyrighted. This site opened:  2018 November 29