Estimating the Incidence of Intelligent Life in the Galaxy
Bruce L. Gary, Last Updated
2023.03.17
I endeavor to show that if the Moon was produced by a grazing collision of proto-Earth by a Mars-sized body, humans are likely to be the only sentient creatures in our galaxy at this time. My argument will rely upon set theory and sampling theory. Keep in mind that this is a “concept demonstration” so it’s not important to have accurate values for the needed parameters.
Now consider the sub-set of this super-set that
have a super-size moon formed by the same process as our moon;
namely, a Mars-sized grazing collision of a proto-Earth. The
Moon’s mass is 1.23 % of the Earth’s mass. For the other solar
system planets the median mass ratio for all satellites of a
planet to the planet’s mass is 0.010 %. In other words, the
Moon’s mass in relation to Eaaaarth is an outlier, being 118
times what would be expected based the other planets. We
Earthlings have a super-sized moon. Here’s a graph that
illustrates this.
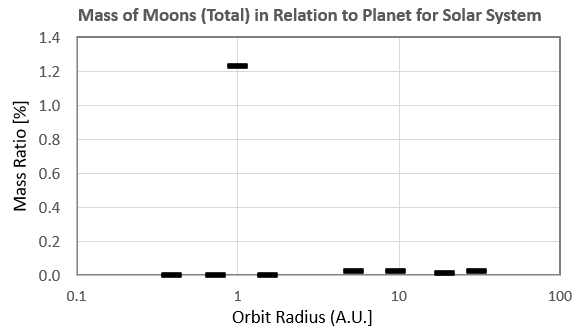
Figure 1. Ratio of sum of masses of moons to the
planet mass for our solar system.
The sub-set of planets with a “super-sized
moon” is a small fraction of the super-set, possibly one in a
million, or 1e-6, leading to a total number for this sub-set of
1e+4. Keep in mind that the fraction of planets that undergo a
Mars-size grazing collision is highly uncertain, but the exact
value is not important for illustrating the important role it
plays in estimating the incidence of life in the galaxy.

Figure 2. The open circles represent a sequence of
100 rocky planets in the HZ somewhere in the galaxy. Tho
filled circles show that two of them have super-sized moons.
Imagine a more realistic diagram in which only about one in a
million rocky planets have a super-large moon.
Now let’s consider a totally different sub-set:
those rocky planets in the HZ that currently have intelligent
life existing on them. This sub-set will be a small fraction of
the super-set, with a large uncertainty. For example, the
fraction may range from 1e-10 to 1e-4. (Note: 1e-10 is a lower
limit given that intelligent life exists on Earth. The upper
limit of 1e-4 is guided by the fraction of time that an
intelligent species exists during the lifespan of the planet,
which for Earth is approximately 300,000 years divided by 4.5
billion years, or 1e-4.)

Figure 3. Illustration of currently existing
intelligent life among the same set of rocky planets in the HZ
shown in the previous figure, assuming no correlation of
super-sized moons with the evolution of intelligent life. For
this illustration only one planet (filled circle) is assumed
to host intelligent life.
We now consider two hypotheses: H1 states that
there is no correlation between these two sub-sets (i.e., the
presence of a super-sized moon is irrelevant to the evolution of
intelligent life), and H2 states that there’s a strong
correlation between these two sub-sets (i.e., that the presence
of a super-sized moon is an essential condition for the
evolution of intelligent life).
Consider that H1 is true. This corresponds to
Fig.’s 2 and 3 being uncorrelated. In other words, if we made a
list of planets with intelligent life on them almost all of them
would have regular-sized moons. Only one-in-a-million would have
a super-sized moon. We humans could have been on any one of the
life-bearing planets, so why are we also on one of those rare
super-sized moon planets? This joint-probability situation is
tremendously unlikely. On any of the Fig. 3 planets with
intelligent life a sentient could ask “How likely is it that we
are residents of both rare and random conditions (we are
intelligent beings on a planet that has a super-sized moon)?”
But we humans have such a super-sized moon, so
we’re stuck with accounting for the improbable situation that we
just happen to be one of those rare intelligent species that
also share the rare condition of having a super-sized moon. The
answer, of course, is that there’s just one chance in a million
that we just happen to be one of those alien species. This is
equivalent to stating that there’s just one chance in a million
that H1 is true; i.e, H1 is probably not true!
Now consider that H2 is true. This corresponds
to a high correlation between Fig.’s 2 and 3. It’s equivalent to
stating that a super-sized moon does something, such as
preserving habitability for a long time so that evolution can
proceed, uninterrupted, to possibly produce an intelligent
species. Whatever the reason for the correlation, we are
permitted to ask one more sampling theory question. “If a
super-sized moon orbiting a rocky planet in the HZ has a
significant probability of producing an intelligent species at
some time during a few billion years interval, and if the
intelligent species lifetime is on the order of 300,000 years,
what’s a likely estimate for N, the number of intelligent
species that now exist in the galaxy?” The answer is obtained by
multiplying the number of rocky planets in the galaxy that are
located in the HZ, 1e+10, by the fraction that have siper-sized
moons, 1e-6, times the ratio of a typical intelligent species
existence to how long it took for that species to evolve,
300,000 years / 4.5 billion years. Doing this yields N = 1e+10 *
1e-6 * 3e+4/4.5e+9 = ~ 0.1. In other words, at the present time
we’re likely the only intelligent species in the galaxy!
This derivation for N is of course dependent
upon the parameter values that go into it. Probably the most
uncertain parameter is the fraction of planets with super-sized
moons. The uncertainty for this parameter could easily be 3
orders of magnitude, leading to the same uncertainty for N.
There’s one loose end in the above that
deserves comment. I adopted a lifetime for an intelligent human
existence to be 300,000 years. That’s how long homo sapiens
has existed. What if humans are going to exist for another 10
million years, for example? That would change the previous
calculation for N, raising it to 2, and we might then be allowed
to believe that we’re not alone because there’s probably another
intelligent species now alive in the galaxy. But this new
assumption requires a violation of sampling theory. This matter
was treated more than 30 years ago, and it sometimes goes by the
name “anthropic principle.” (I independently discovered this
idea a few years later and was teased at the JPL cafeteria when
I explained it to my astronomer friends.) It goes like this: So
far there have been ~ 70 billion human lives lived. The total
number of humans that will ever live can be estimated by
assuming we’re now not at a privileged position on that
sequence. So, there’s a 50 % probability, according to sampling
theory, that the total number of humans that will ever live is
140 billion (i.e., double 70 billion). But given our past global
population, and given reasonable projections for the future
(e.g., leveling off at ~ 12 billion), 140 billion lives will be
reached in less than 200 years.
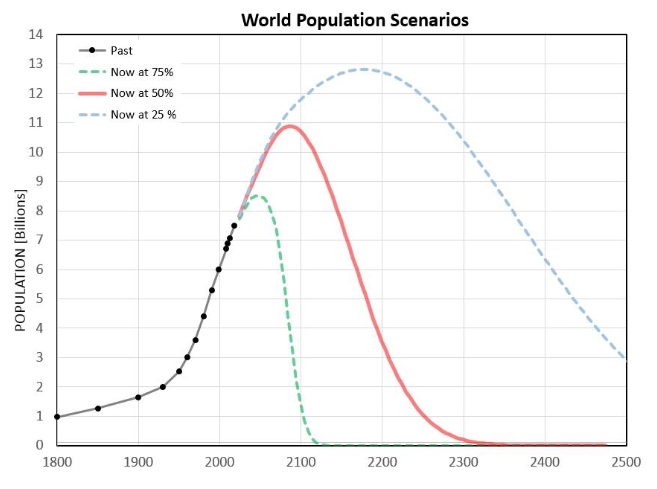
Figure 4. Three scenarios for future
world population, corresponding to our present time being
at the 75th, 50th and 25th
percentiles of the entire human sequence.
Therefore, humanity must be near its end, so
it's fair to assign humanity a 300,000-year lifespan, and,
finally, we are probably alone in the galaxy.
The previous “armchair calculations” show how
important it is to obtain a more accurate estimate for
super-size moon creation by grazing collisions of Earth-size
proto-planets by Mars-size planetesimals. People engaged in SETI
projects might want to consider this.
Return to Main web page
____________________________________________________________________
This site opened 2023.03.16. Nothing on this
web page is copyrighted.