There continues to be a need for all-sky photometry because some catalogs have erroneous entries. For example, during my asteroid observing I've seen on a couple occasions an abrupt change in APASS-based asteroid magnitude followed about a 1/2 degree of motion later by a recovery to the original magnitude. This means that small regions of the APASS catalog can have systematic errors on the order of 0.1 magnitude. I have also seen occasional discrepancies in color/color scatter diagrams using APASS magnitudes. Most APASS magnitudes are good, with r'-mag agreeing with CMC14 (for example) at < 0.010 magnitude. I estimate that when there are no systematic errors the APASS r'-mag's exhibit an internal consistency that is slightly better than CMC14, or ~ 0.015 magnitude. However, when there is a scientific need using a good quality magnitude I think it is important to conduct an all-sky observation.
Introduction
There are several ways to achieve an all-sky
photometry solution, and depending on what can be assumed some
are simpler than others. The basic equation governing all such
solutions will be demonstrated using V-band:
V-mag = Zv -2.5 × LOG (flux/g[sec]) - Kv ×
AirMass + Sv × StarColor + Sv2 × AirMass
× StarColor
(1)
where the blue symbols are a property of the
telescope system and atmosphere are assumed constant during an
observing session. Exposure time is given as "g[sec]" and
StarColor can be defined in any way you want, such as "B-V" or
"B-V-0.64" or "0.57×(B-V)"
- 0.33" (my preferred definition). Atmospheric extinction is
Kv, with units of [mag/AirMass). Flux is measured with a large
photometry aperture, such as 4 × FWHM.
The all-sky procedure is used to evaluate the
four blue constants from an observing session during
"photometric sky conditions" (i.e., no clouds, no wind and no
dew prospects). The observing session should involve several
star fields with well-calibrated stars alternating with the
target star field, all at the same air mass (except for one or
two calibrated star fields observed at a much different air
mass, to permit an estimate of approximate atmospheric
extinction for the observing session). The well-calibrated
star fields will be those created by Arlo Landolt, whose
heroic project led to the adopted standard of 1259 stars for
B, V, Rc and Ic bands. If u'g'r'i'z' magnitudes are involved,
then the 158 well-calibrated stars in the Smith et al (2002)
database will be used. The Smith et al stars are a subset of
the Landolt set (most located along the celestial equator).
Simplest Possible All-Sky Procedure
Note that if the well-calibrated star fields
are observed at the same air mass (which I'll refer to as
"m"), the above equation can be simplified by removing the
third term, the involving only air mass times a constant. Note
also that if only well-calibrated stars are used with the same
StarColor as the target star, then the last two terms can also
be removed. That would leave:
V-mag = Zv
-2.5 × LOG
(flux/g[sec])
(2)
Let's demonstrate use of this two-term equation
for the target star KIC846 (short-hand for KIC8462852) using
observations I made on 2016.09.05 with my Meade 14" and SBIG
ST-10XME CCD. The observing session lasted 2 hours, and
included 6 Landolt star fields (25 stars). The target field
was observed 4 times, between the Landolt star fields. KIC846
has a B-V estimated to be +0.53 ± 0.02 (APASS gives +0.508 and
Tabby's Table 3 gives +0.557). Lets look for a Landolt star
with the same B-V. Star SA110.506 has Landolt V = 11.312 and
B-V = +0.568, which is close. My first image of this star
field (AirMass = 1.166) has a measured flux for this star of
138,550 counts (using a photometry aperture 4 × FWHM, g[sec] = 20
sec). This allows us to derive an
approximate value for Zv:
Zv = V-mag + 2.5 ×
LOG (flux/g[sec])
(3)
Zv = 11.312 + 2.5 ×
LOG (138550/20) = 20.913, which means that (rewriting eqn 2):
V-mag = 20.913 -2.5 × LOG (flux/g[sec])
A few minutes later I took an image of the
KIC846 star field (AirMass = 1.067, same exposure time). Flux
was measured to be 80669 counts. Using the above eqn. yields:
V-mag
= 20.913 -2.5 × LOG (80669/20) = 11.899
That's a quick estimate of KIC846's V-mag. We
could use averages of fluxes from more than one image, and
propagate errors to derive a SE for this V-mag estimate. And
we could apply small corrections to the inexact matches of
AirMasses and B-V star colors, but that would require knowing
atmospheric extinction at V-band on this date and star color
sensitivity. That's what's done in the next section. But
before we do something more sophisticated, let's compare this
V-mag determination with others in the literature.
APASS DR9 gives KIC846's V-mag = 11.852 ±
0.046. Tabby's Table 3 gives V-mag = 11.705 ± 0.017. This quick estimate differs by +0.047 ± 0.055 (est'd SE) and +0.197 ± 0.034 (est'd SE),
where I've adopted a SE of 0.030 for my quick estimate. (A
more careful analysis of my all-sky measurements, see below,
yields V-mag = 11.912 ± 0.012, which corresponds to the quick
method differing by -0.013.)
A Slightly More Sophisticated All-Sky
Procedure
Let's improve on the previous procedure by
using more Landolt calibration stars, and averaging images
before measuring flux. We can also apply approximate
corrections for non-identical AirMass matches. However, we
don't want to use Landolt stars that are greatly different in
color, so let's look at a scatter diagram of V_mag and
StarColor for the Landolt stars that were measured during the
2-hour Sep 05 all-sky observing session:
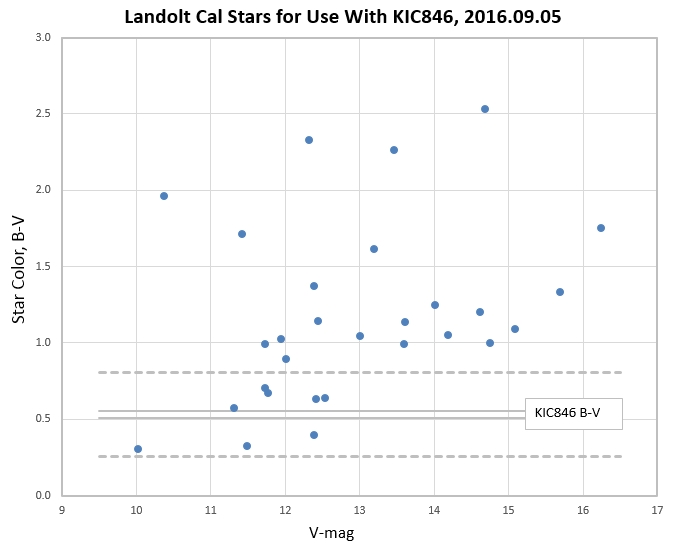
Figure 1. Star color (B-V) vs. V-mag for 25 Landolt stars observed during the Sep 05 all-sky observing session. The closely-spaced horizontal lines indicate two estimates of KIC846's B-V. The dotted lines indicate what B-V range I will accept for use in the following analysis; it includes 8 Landolt stars.
Here's the plan: We will repeat the analysis in the previous section for each of the 8 Landolt stars. In addition, we will use a flux measurement from the average of ~ 20 images for each Landolt star. We will then choose a set of KIC846 images for obtaining the target star's flux. We will then apply a simple adjustment for the difference in air mass of the Landolt and target star, using an assumed atmospheric extinction (which was determined from the Landolt stars).
For each of the chosen 8 Landolt stars we will evaluate Zv using eqn (3). The results are shown in the next figure.
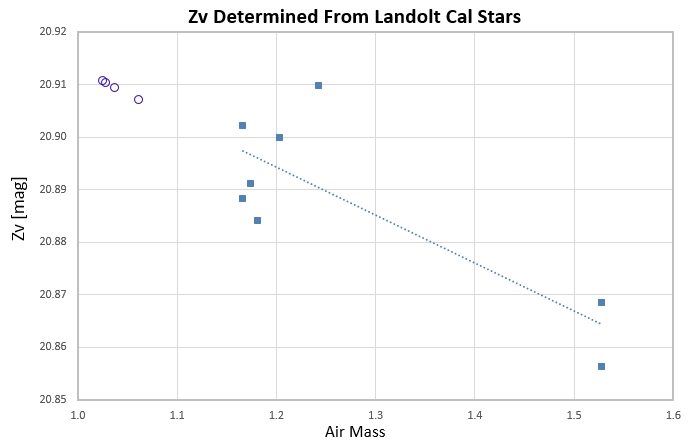
Figure 2. Zv, calculated from eqn (3) for 8 Landolt stars with star color similar to KIC846. There's a dependence upon air mass, which is extended to the air mass region of the KIC846 observations (open circles).
The air mass dependence is due to ignoring the 3rd term in eqn
(1): Kv × AirMass.
The slope of the fit can be used to evaluate Kv, which is ~ 0.10
mag/airmass. (This is close to the more elaborate analysis, in
the next section, yielding Kv = 0.11 mag/airmass.)
What is the air mass for KIC846 observations? They range from
1.026 to 1.062, as shown in Fig. 2. Since the Zv placement of
the KIC846 air mass symbols (open circles) is based on the trend
line for the Landolt stars, we can easily see what Zv values
should be used for processing the KIC846 flux measurements. The
average Zv for use with KIC846 is 20.909.
Eqn. (2) can be used to convert measured flux for KIC846 to
V-mag.
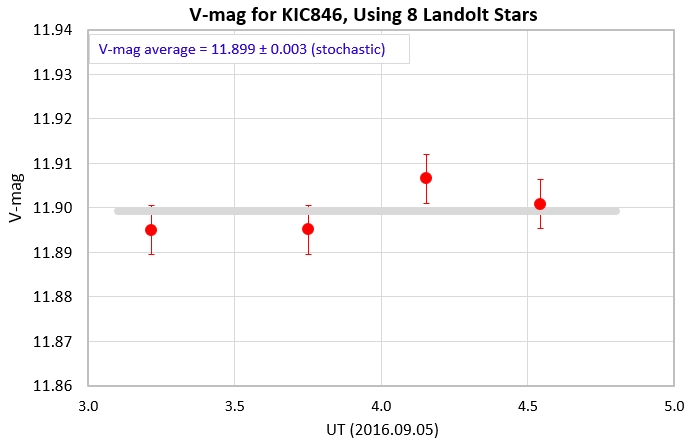
Figure 3. V-mag results for KIC846 using the Zv
values determined in the previous figure.
The V-mag results shown in the above figure are the same as
determined in the first section of this web page, V-mag =
11.899, based on just one well-chosen Landolt star and one
KIC846 image. At least we know that many measurements of both
Landolt stars and KIC846 are telling the same story. It's always
risky to use a single image (with possibly cosmic ray artifact)
for anything quantitative.
We should now ask what terms in the complete magnitude equation
(1) have been neglected, and which require adjustment for the
above V-mag result. Here's a repeat of eqn. (1):
V-mag = Zv -2.5 × LOG (flux/g[sec]) - Kv × AirMass + Sv × StarColor + Sv2 × AirMass × StarColor (1)
The 1st and 2nd terms have been handled
properly. Since we used Zv values appropriate for the KIC846
air mass for the 4 KIC846 observing groups (of 20 images each)
we have taken into account the effect of the 3rd term: AirMass
×
Kv. The last two
terms were handled with approximate appropriateness by
choosing for use only the Landolt stars with both StarColor
and AirMass similar to KIC846. Still, let's consider the
level of systematic errors that could result from a more
explicit treatment of star color. When a V-band filter
is used to measure V-mag it is common for the star color
term, Sv, to be ~ 0.1 mag/mag (assuming use of B-V to
define star color). In fact, a more sophisticated
analysis (next section) shows that Sv = 0.077. The
average B-V StarColor for the 8 Landolt stars used in
this section differ from the best estimate of KIC846's
B-V star color by ~0.03 mag. Therefore, assuming our
estimate for KIC846 B-V StarColor is correct, the
systematic SE for our V-mag derivation should be <
0.003 mag. But our estimate for KIC846's B-V star color
is uncertain by ~ 0.10 mag (the two estimates differ by
0.05 mag). Therefore, we should
allow for a systematic error uncertainty of ~ 0.008 mag in our
V-mag derivation. Orthogonal addition of 3 mmag and 8 mmag
yields ~ 9 mmag.
The last term shouldn't contribute
significantly to the systematic error in our procedure because
both delta-AirMass and delta-StarColor are small, and they are
multiplied in eqn (1), so their product should be even
smaller.
Landolt star mag's at V-band exhibit a scatter
(in my sophisticated solution, below) of ~ 0.005 mag in the
V-mag 12 region. This will be my estimate of Landolt
systematic SE. We can now orthogonally add the several
components of estimated systematic error SE: 5 mmag (Landolt
V-mags), 3 mmag (internal scatter for Fig. 3) and 8 mmag
(KIC846 star color SE). The resultant SE is 10 mmag.
Therefore,
KIC846 V-mag = 11.899
± 0.010
This result takes into account all terms in the
fundamental magnitude equation (1).
A More Sophisticated All-Sky
Derivation
Each flux measurement, whether for KIC846 or a
Landolt calibration star, can be compared with a model (eqn 1)
for calculating a difference, whoose sum for all measurements
can be minimized using chi-square concepts. This is easily
implemented in a spreadsheet, but describing the details is
beyond the scope of this web page treatment. I will instead
show graphs produced by this procedure.
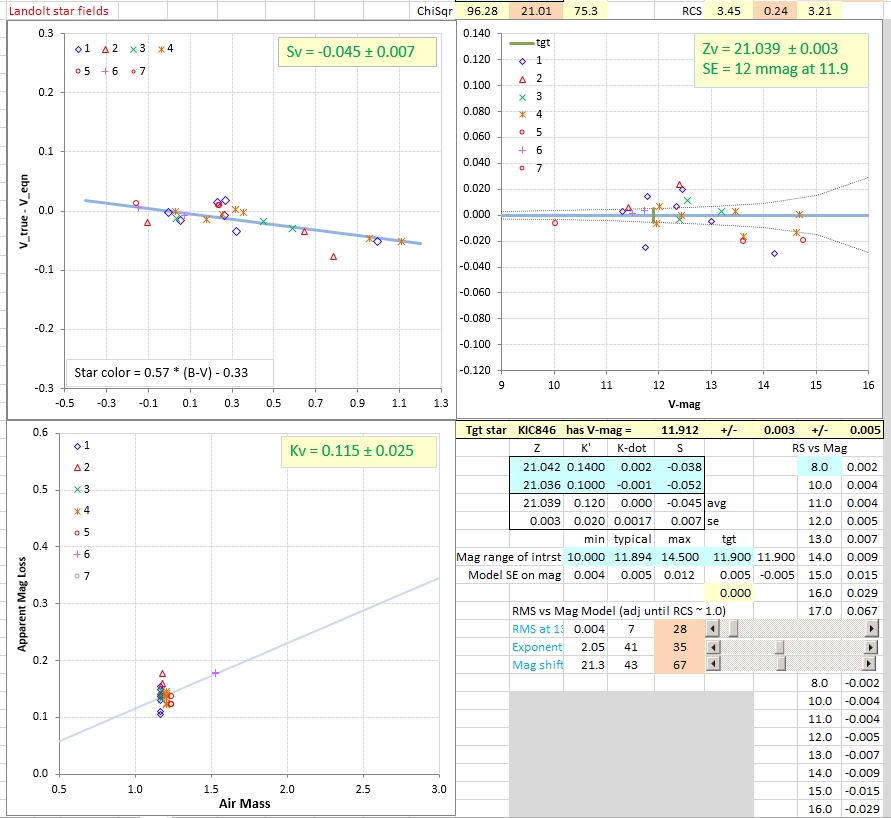
Figure 4. Summary of results using a complete implementation of Eqn (1) analysis of KIC846 and Landolt star observations.
The upper-left panel of Fig. 4 illustrates the
dependence of Landolt star V-mag vs. star color. The fitted
slope is the model solution, which invokes a star color
sensitivity parameter, Sv = -0.045 ± 0.007 [mag/mag].
The lower-left panel is used to solve for
Landolt star V-mag dependence upon air mass, with the sloped
fit line being atmospheric extinction: Kv = 0.115 ± 0.025
mag/airmass.
The upper-right panel is used to solve for Zv
in a way that allows for the fact that model comparisons for
faint stars is less important than for bright stars. The
solution is Zv = 21.039 ± 0.003 mag.
As shown in Fig. 4 the V-mag solution for
KIC846 is V-mag = 11.912 ± 0.003 (stochastic SE). This differs
from the previous section's solution by 0.013 ± 0.005
(stochastic) ± 0.012 (total SE) mag. In other words, the two
procedure give V-mag answers that are compatible with each
other.
This spreadsheet allows for the simultaneous solution for V-mag for many stars in the KIC846 field, 25 in this case. The following graph shows how my V-mag's for the KIC846 field of 25 stars compares with the APASS V-mag's.
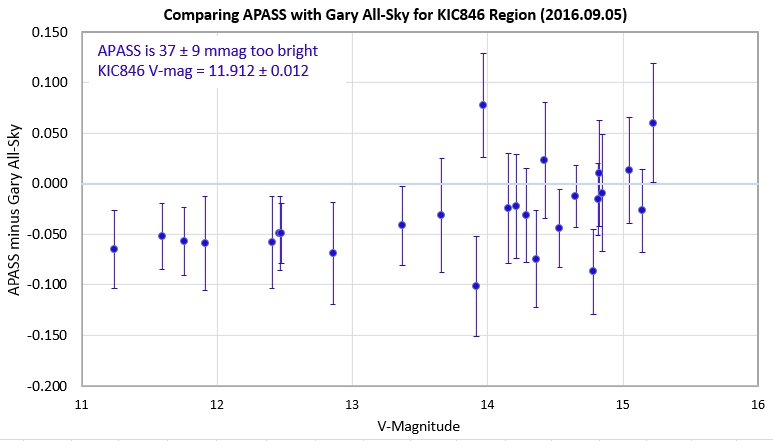
Figure 5. Comparing APASS DR9 V-mag's with
my all-sky derivations.
I claim that the APASS V-mag's for this star
region are too bright by 0.037 ± 0.009 mag. This is
statistically significant, yet small compared with the 0.207 ±
0.021 mag difference with the Table 3 entry of Boyajian
et al, 2015.
Conclusion
Three methods have been demonstrated for performing all-sky
photometry, and each gives a result that is compatible with the
others. For this particular case, KIC846, it was found that
V-mag is fainter than reported in Boyajian et al, 2015, by 0.207 ± 0.021 mag. It remains to be determined if
this represents a fade during the 2.2-year interval between
observations.
Boyajian et al, 2015, MNRAS, "Planet Hunters X. KIC
8462852 - Where's the flux?" link
Smith, J. Allyn et al, 2002, AJ, 123, 2121-2144